5.5. Resonance

Some molecules can be represented as different Lewis or line-angle structures that have the same placement of atoms but a different placement of electrons. These are referred to as resonance structures (Figure 5.20). For example, there are two ways to draw the double bonds in 1,2-dimethylbenzene (o-xylene), and three different ways of representing N,N-dimethylformamide. The structures are related to each other using the double headed arrow for resonance (Table 5.1)

Figure 5.20 – Examples of Resonance Structures.

Which way is correct? There are two answers to this question: ‘all’ and ‘none’. Each way of drawing the molecule is an equally acceptable approximation, but none of them, by itself, is an accurate picture of the molecule. However, when considered together they give a much more accurate picture than any on its own. This is because they imply, together, that these bonds are not double bonds, not single bonds, but something in between. Sometimes this is represented using dotted bonds, or a circle in the case of aromatic compounds (Figure 5.21). These are common in biochemistry but are heavily discouraged in this text. When represented in these ways it becomes easy for students to lose track of how many electrons (lone pairs and π bonds) are being shown.

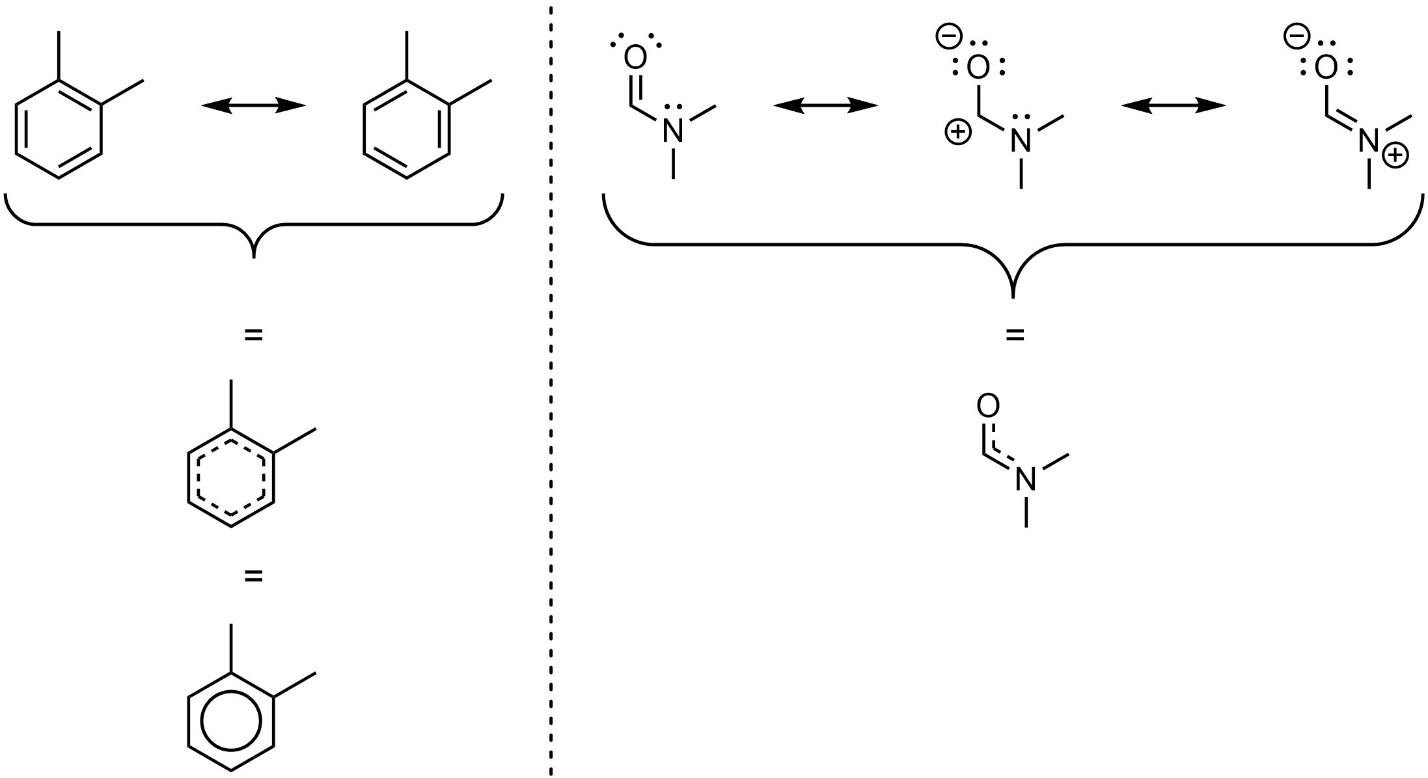
Figure 5.21 – Alternate Representations of Resonance Structures.

Resonance is a graphical tool to approximate the ‘real’ distribution of electron density in the molecule. Curved arrows are often used to make it easier to understand the relationship between the two (or more) structures (Figure 5.22). They represent imaginary electron movement between the resonance forms. Resonance is not a physical process. The electrons are not moving along the paths of the curved arrows. The molecule does not look like one form one second and the other the next. The molecule looks like a weighted superposition of all resonance forms at once.

Figure 5.22 – Examples of Curved Arrows in Resonance Structures.

5.5.1. Stabilization by Resonance/Delocalisation

Because the electron density is shared over multiple atoms, resonance is sometimes referred to as delocalisation (the electrons are not longer “localized” to a specific atom or bond). Having multiple resonance forms provides a large amount of stabilization. The more resonance forms a group or molecule has, the more stability it gets. Why this is true is complicated, but the most important benefit is simple: the bonds between the atoms involved become stronger. For example, as a result of having multiple resonance forms, the highlighted N-C bond in the left structure is (much) stronger than the corresponding one in the right (Figure 5.23). Since the energy in bonds is part of enthalpy (ΔH) and enthalpy is part of free energy (ΔG), having stronger bonds provides stability to the molecule.

Figure 5.23 – Comparison of Bond Strength with and without Resonance.

5.5.2. Requirements for Having Resonance Forms

There are several features that make having resonance forms possible. Since having resonance forms provides a large amount of stabilization, if a molecule can have them, it almost certainly will. It may be initially beneficial to memorize these patterns, but with sufficient practice it is not necessary.

Resonance is possible if there is a polar π bond (Figure 5.24). This is most commonly found in the form of a carbon double or triple bonded to a heteroatom such as oxygen or nitrogen.

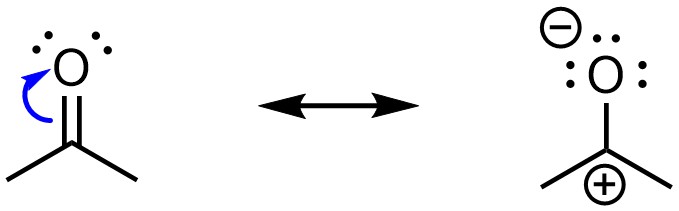
Figure 5.24 – Example of Resonance from a Polar π Bond.

Resonance is possible if there is a π bond directly connected to an atom with a lone pair (Figure 5.25). The lone pair can be from a heteroatom or from an anion. At an introductory level, assume halogens do not work for this type of resonance.

Figure 5.25 – Examples of Resonance from a π Bond Directly Connected to an Atom with a Lone Pair.

Resonance is possible if there is a π bond directly connected to an atom with an incomplete octet (Figure 5.26). This is most commonly found in the form of a carbocation, though other cations are possible.

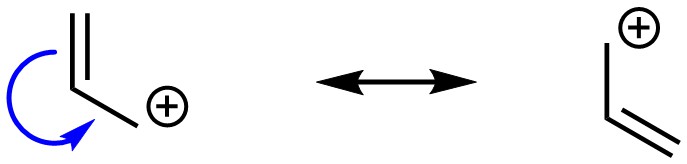
Figure 5.26 – Example of Resonance from a π Bond Directly Connected to an Atom with an Incomplete Octet.

Resonance is possible if there is a π bond directly connected to another π bond (Figure 5.27). This may include adjacent alkenes. Note that this is NOT equivalent to an atom with π bonds to two different atoms. Resonance in these cases is not possible due to the orbitals involved being orthogonal.

Figure 5.27 – Example of Resonance from a π Bond Directly Connected to an Atom with Another π Bond.

Finally, resonance is possible if there is an atom with a lone pair directly connected to an atom with an incomplete octet (Figure 5.28). This is most commonly found in the form of a heteroatom adjacent to a carbocation.

Figure 5.28 – Example of Resonance from an Atom with a Lone Pair Directly Connected to an Atom with an Incomplete Octet.

Even in complex molecules, recognizing how smaller sub-sections of the molecule resemble the basic examples above can be used to help construct additional resonance forms (Figure 5.29).

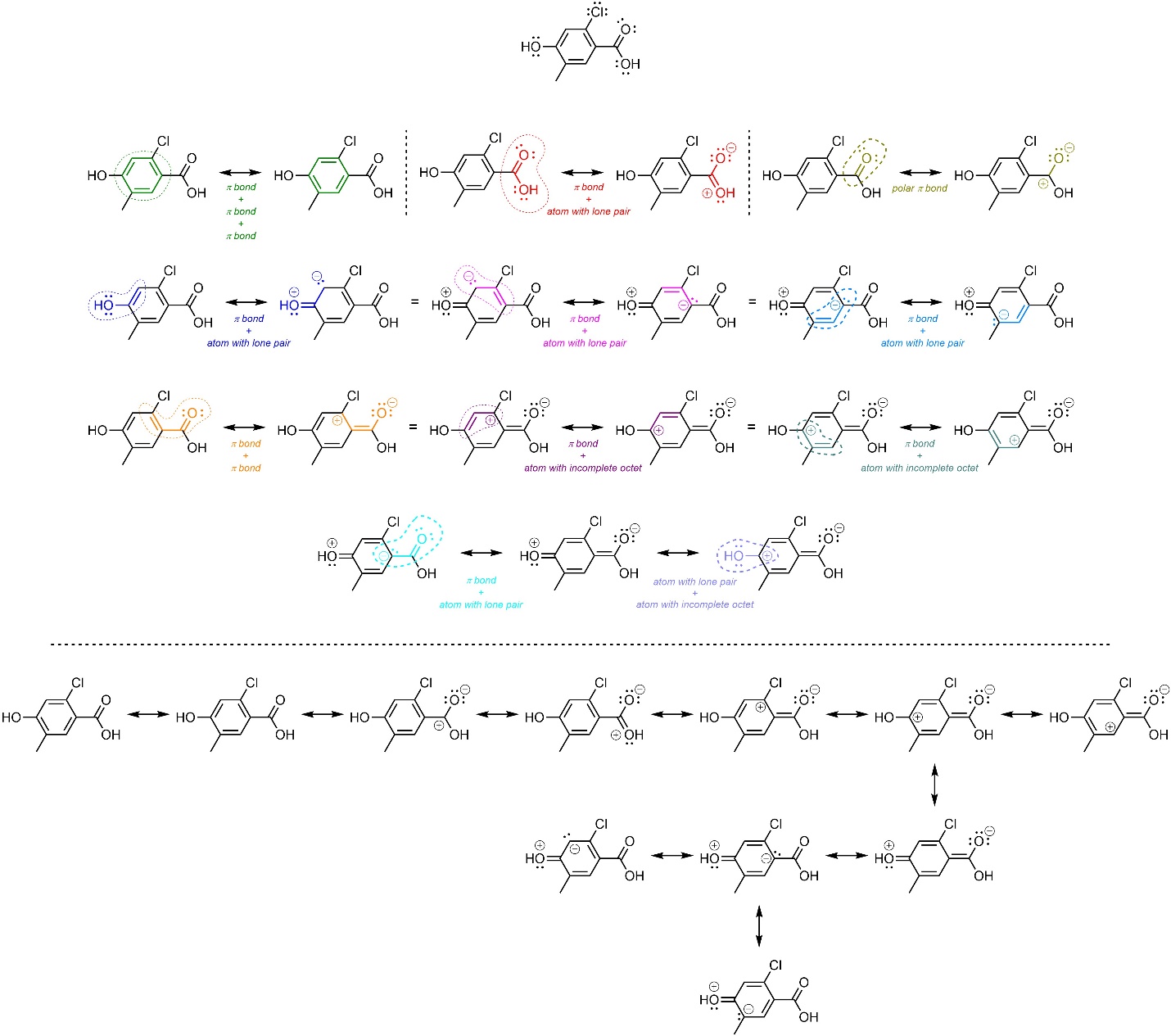
Figure 5.29 – Example of Applying Features Leading to Resonance to a Complex Molecule.

5.5.3. General Tips for Drawing Resonance Structures

Always draw in all lone pair electrons before attempting to generate any resonance structures. This is very helpful for seeing which areas satisfy the conditions needed and ensures no areas will be overlooked.

When generating resonance structures the arrangement of atoms remains unchanged. This is the second most common mistake and can be a quick way to recognize that two structures are not resonance forms (Figure 5.30).

Figure 5.30 – Resonance and Not Resonance from Movement of Atoms.

When generating resonance structures σ bonds are not moved. Technically, an effect similar to resonance of σ bonds is possible. This is referred to as hyperconjugation and is usually considered too advanced for introductory material.

When generating resonance structures lone pair electrons and π bonds (double and triple bonds) can be moved. A π bond can be moved to create another π bond. Lone pairs can become π bonds, and π bonds can become lone pairs.

When generating resonance structures DO NOT BREAK THE OCTET RULE. This is the most common mistake (Figure 5.31). Remember that it is possible to have less than 8 electrons (an incomplete octet), but not more.

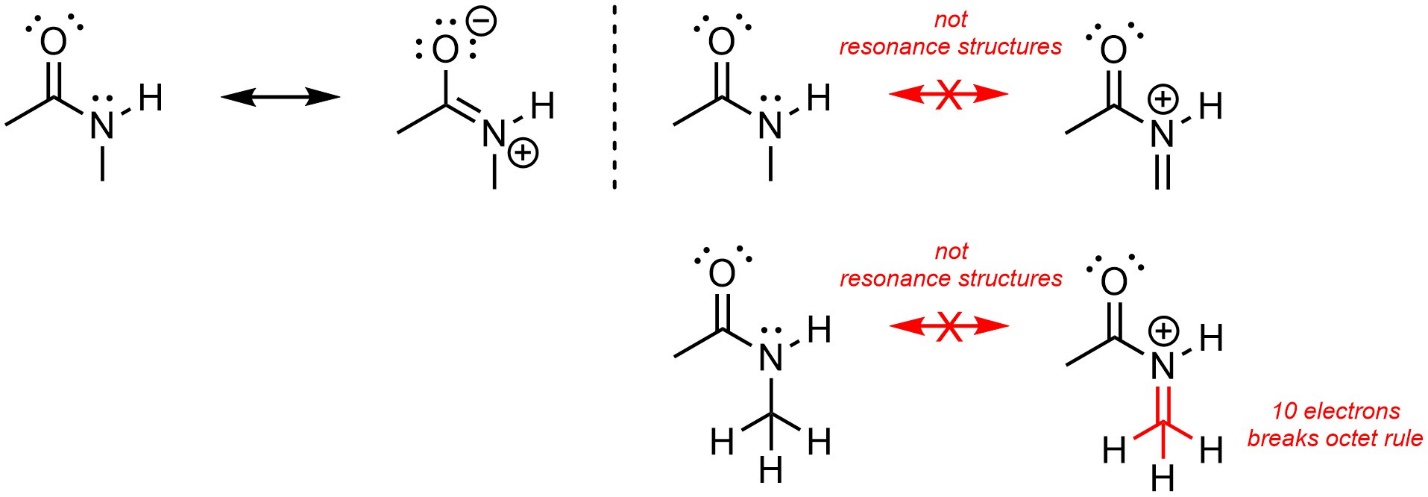
Figure 5.31 – Resonance and Not Resonance from Broken Octet Rule.

When generating resonance structures the overall charge does not change. If the molecule is neutral in one resonance form, then it will be overall neutral in all resonance forms. Formal charges (cations and anions) are allowed but must cancel out so that the overall charge is unchanged. For example, charges are visible on the resonance forms above (Figure 5.29) but in all of them the molecule is overall neutral.

The following advice must be considered carefully. When generating resonance structures usually do not make adjacent or unusual charges. Having a cation adjacent to an anion is often acceptable, though in general they should match with the electronegativity difference (i.e. the anion should be on the more electronegative atom). However, having two anions/cations adjacent to each other is (probably) not a reasonable resonance structure (Figure 5.32). Generating a doubly cationic or anionic atom (+2 or -2 formal charge) is even less reasonable. In more advanced texts some molecules may have exotic electron configurations. For example, carbenes have a lone pair and an incomplete octet and are usually viewed as being both cationic and anionic on the same atom at the same time. For the purposes of this text, unusual charges such as this are not acceptable resonance structures. Examples with them will not feature in this text.

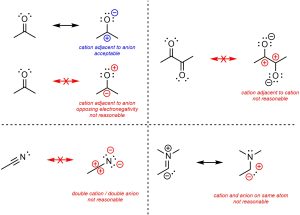
Figure 5.32 – Examples of Unreasonable Resonance Forms from Adjacent or Unusual Charges.

5.5.4. Evaluating Contributions of Resonance Forms

The overall picture of a molecule is a weighted average of all of its resonance forms. The weighting refers to how much a given resonance form contributes to the total image. Resonance forms do not all contribute equally (although some can). It is possible to compare and rank contribution from multiple resonance forms. In decreasing order of importance, higher-contribution forms have:

• The most atoms with full octets.
• The fewest formal charges.
• Negative formal charges on more electronegative atoms.
• Positive formal charges on less electronegative atoms.
• Similar charges are as far apart as possible.
• Opposite charges are as close as possible.

It is possible to rank many resonance forms, such as those above (Figure 5.29). This is more tedious than challenging and would not be expected at an introductory level. It is more reasonable to expect comparisons of a handful of resonance forms (Figure 5.33).

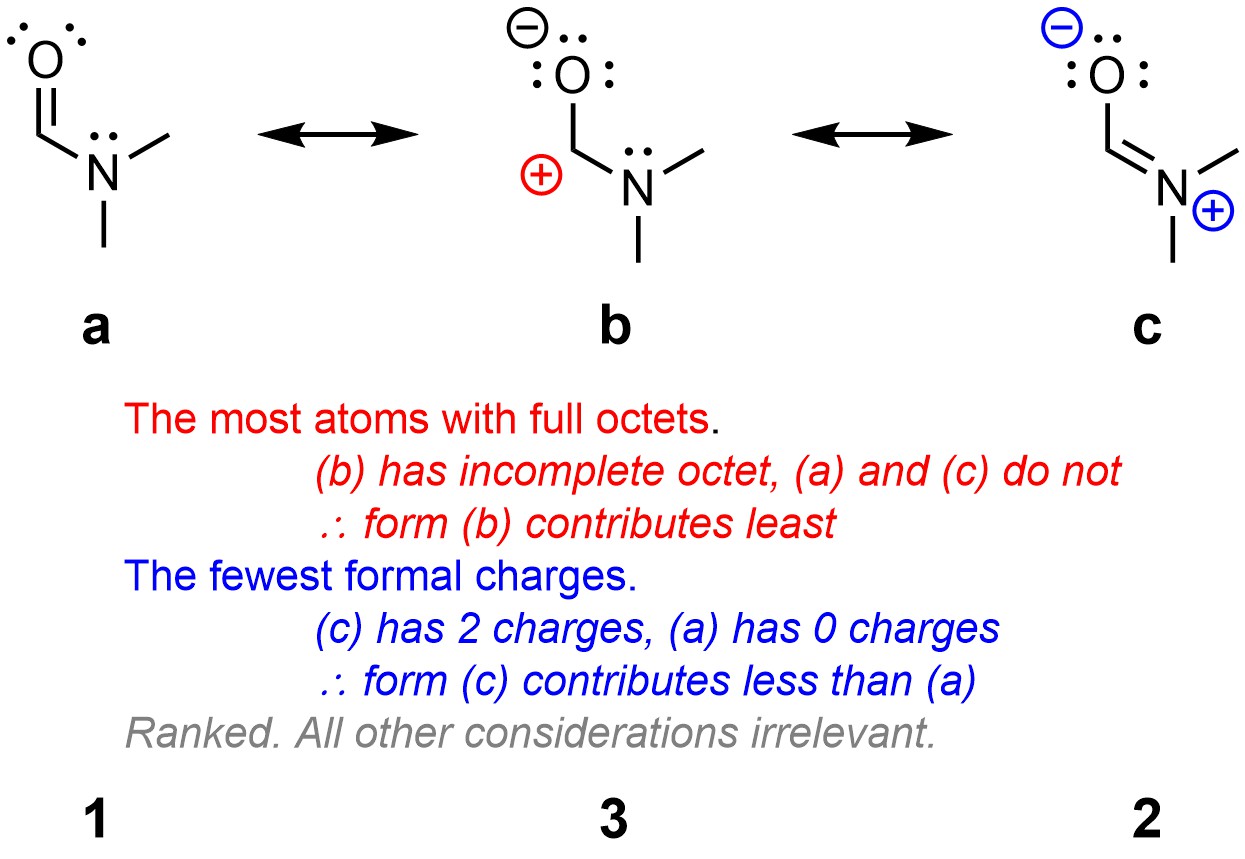
Figure 5.33 – Comparison an Ranking of Resonance Forms of N,N-Dimethylformamide.

If many of the factors above are violated a resonance form can be “ruled out” or classed as unreasonable (Figure 5.34). Some sources may refer to this as determining whether or not a proposed resonance form is significant (i.e. it contributes a significant amount to the ‘real’ image of electron distribution), or not. In this case the middle resonance form would not be considered significant because it violates multiple factors.

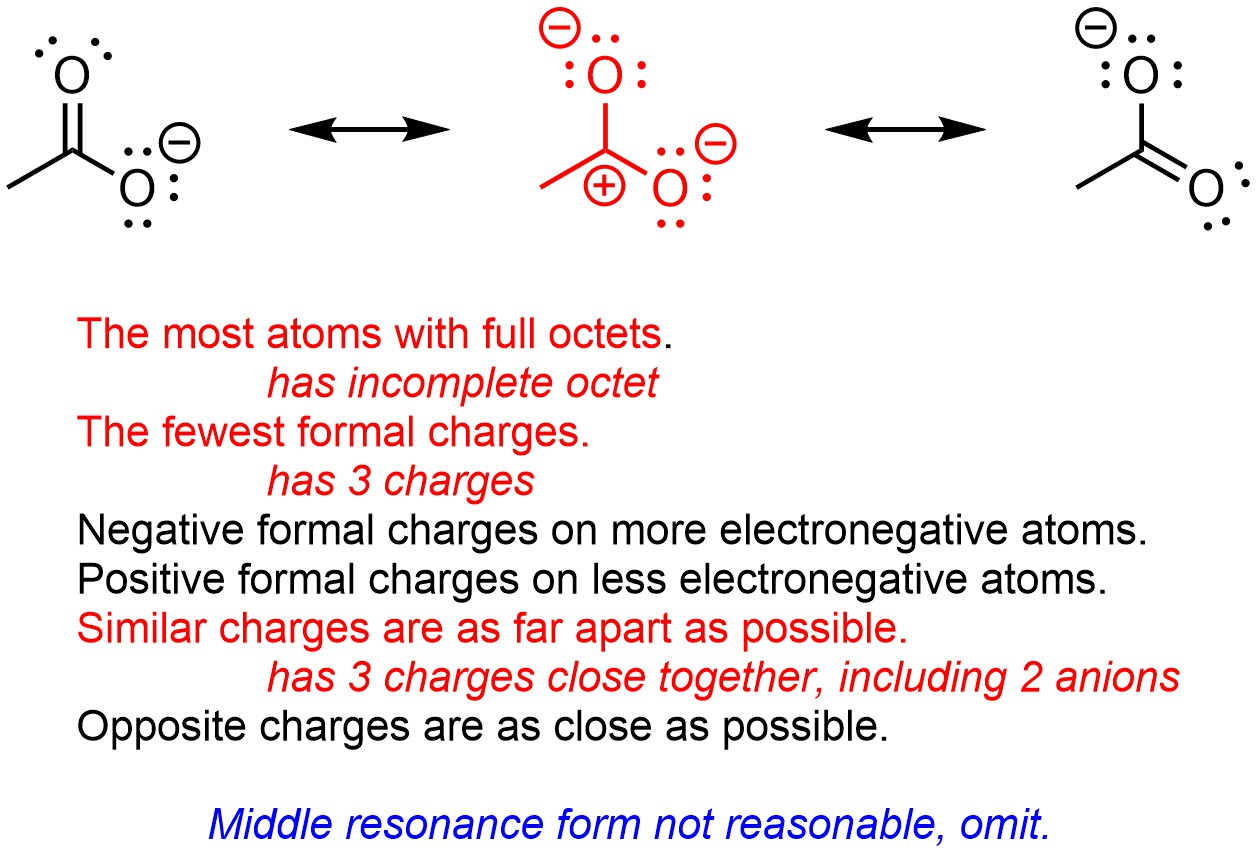
Figure 5.34 – Classifying a Resonance Form of Acetate as Unreasonable.

It is important to remember that resonance forms can contribute equally if all factors are equivalent (Figure 5.35). They may then be ranked relative to the other forms, if any.

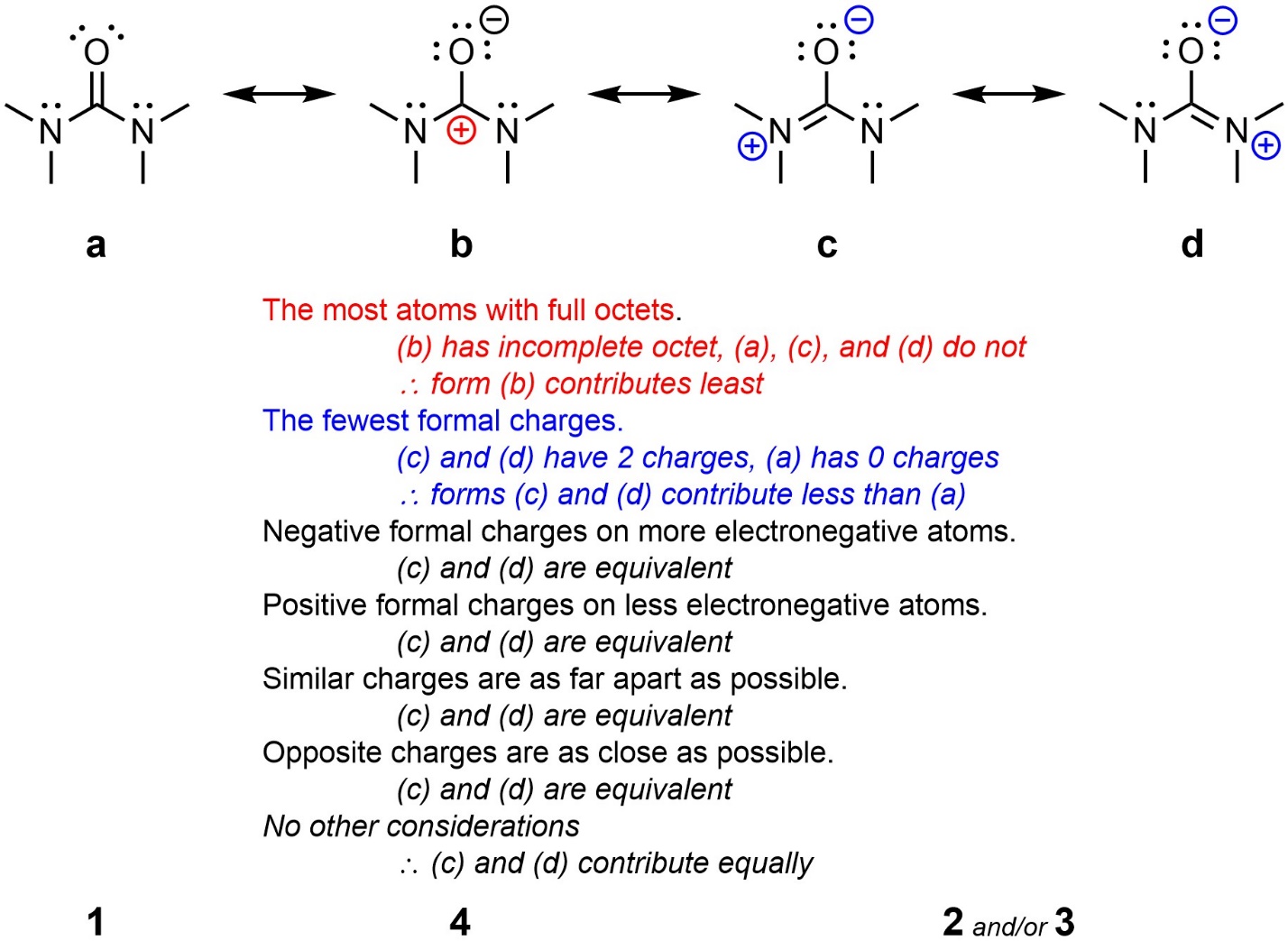
Figure 5.35 – Comparison and Ranking of Resonance Forms of 1,1,3,3-Tetramethylurea.

5.5.5. Visualizing Orbitals and Resonance

Recall that resonance is a graphical tool to approximate the ‘real’ distribution of electron density in the molecule. This can be approximated using dotted bonds, though this approach is discouraged. Alternatively, delocalized systems can be visualized by overlapping all conjugated p orbitals (Figure 5.36). This approach is useful for seeing how the electron cloud is distributed over the entire set of atoms involved, but can be challenging for students to draw at an introductory level.

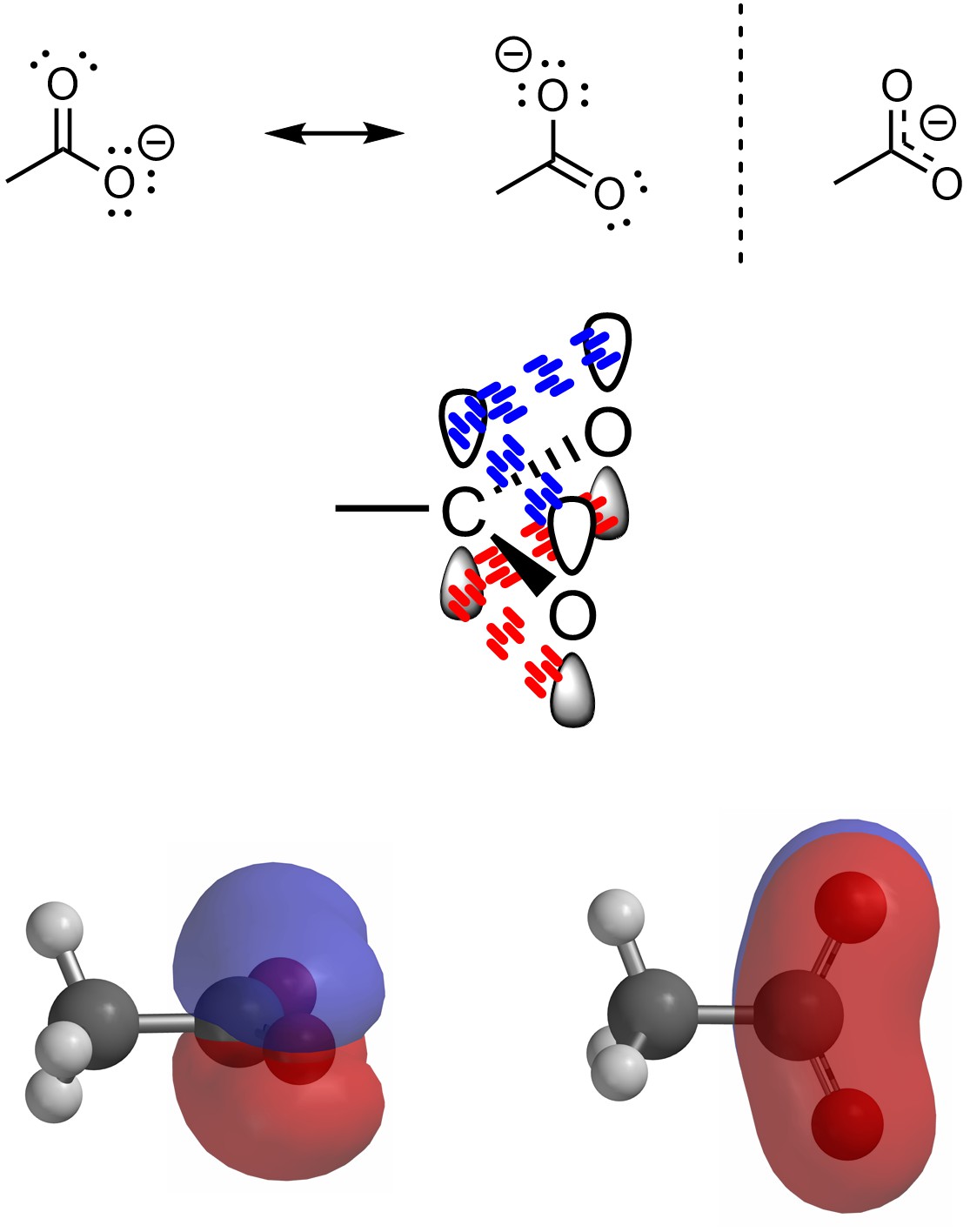
Figure 5.36 – Visualizing Orbitals and Resonance in Acetate.

5.5.7. How to Determine the Hybridization of an Atom with Multiple Resonance Forms

Depending on which resonance form is depicted the hybridization of atoms may appear to change. For example, the nitrogen in N,N-dimethylformamide appears to be sp³ hybridized in the (a) and (b) forms, but sp² hybridized in the (c) form (Figure 5.37). The oxygen appears to be sp³ hybridized in the (b) and (c) forms, but sp² hybridized in the (a) form. Conversely, the central carbon is sp² hybridized in all three forms.

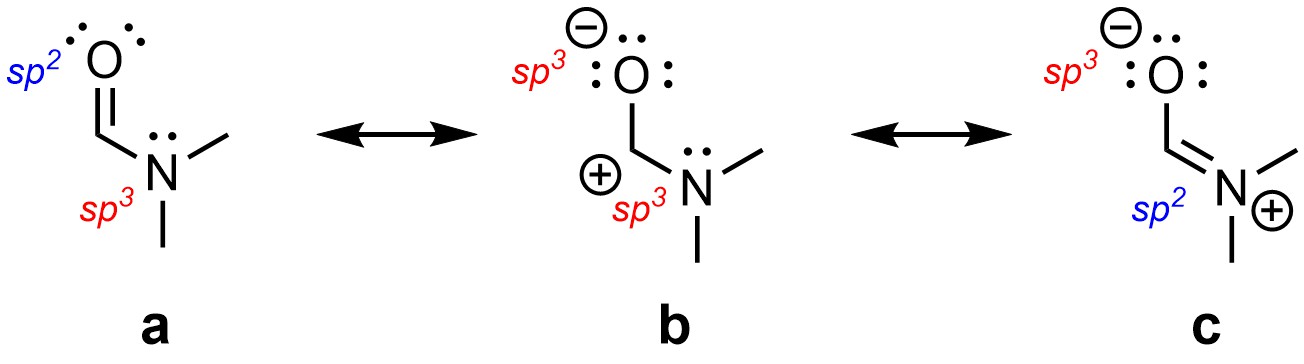
Figure 5.37 – Apparent Hybridization of Atoms in Resonance Forms of N,N-Dimethylformamide.

In reality all three have trigonal planar geometries; all three atoms can be classed as sp² hybridized. Recall that resonance is highly stabilizing. All three atoms require p orbitals to form a delocalized electron cloud (as in Figure 5.36). It is not possible to have an available p orbital and be sp³ hybridized. They all adopt sp² hybridization to be able to participate in resonance.

This is true of any molecule that has multiple resonance forms. Technically, each atom has the hybridization with the highest s character from all its resonance forms. This wording is often confusing at an introductory level. An alternative phrasing is “each atom has the hybridization made from the fewest p orbitals of all its resonance forms”. For example, the nitrogen and oxygen above appear to be either sp² or sp³. The sp² orbitals are made from an s orbital and two p orbitals. The sp³ orbitals are made from an s orbital and three p orbitals. Two is smaller than three, so the hybridization on carbon, nitrogen, and oxygen above is sp² instead of sp³.