4.7. Optical Rotation
Identifying and distinguishing enantiomers is inherently difficult because their physical and chemical properties are identical. However, that they interact with polarized light differently may be used for this purpose.
4.7.1. How Optical Rotation Works
A background on the properties of light is helpful for understanding the process being exploited. This text is not an introduction to physics, so a detailed understanding of all the concepts in this area is not required.
Light is made of photons, which are wave-particles. As light travels the photons oscillate (move back and forth along an axis perpendicular to the one they are travelling along). This means that light’s path though space looks like (very tiny) sine functions when viewed from the side (Figure 4.40).
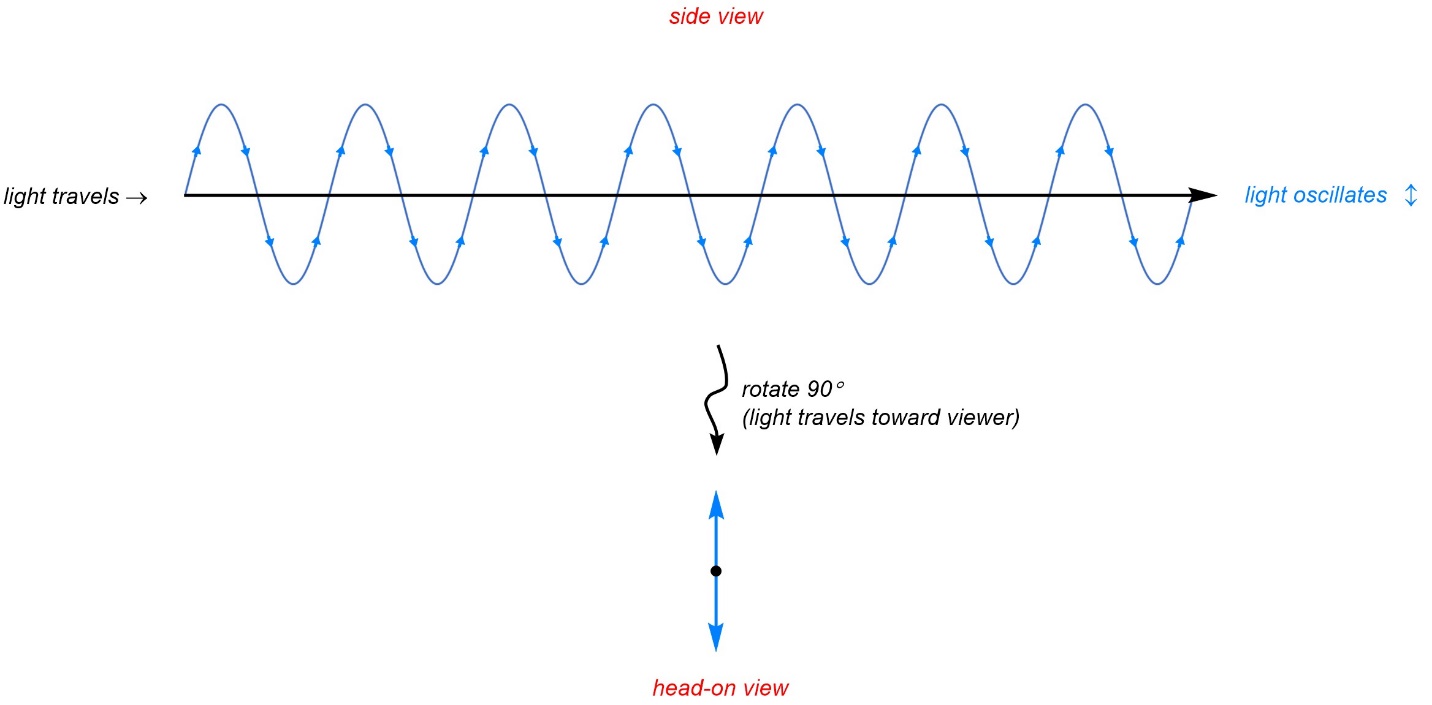
Figure 4.40 – Electric Field Component of Light Travelling Through a Media.
If instead of looking at the path of light from the side it is viewed head-on, the light appears to travel back and forth between two points and can be approximated using a double headed arrow. Normal light from a source such as the sun or a lightbulb is randomly oriented as it travels (Figure 4.41). Each photon will oscillate along a random axis perpendicular to the one they travel along. However, if a plane-polarizing filter is placed in the path of the light only photons aligned with the filter’s axis can pass through. This makes the light polarized in a certain plane (all the photons are oscillating in the same plane/axis). These filters can be made several ways, but functionally they are very tiny slits in a material arranged parallel to each other in the desired direction.
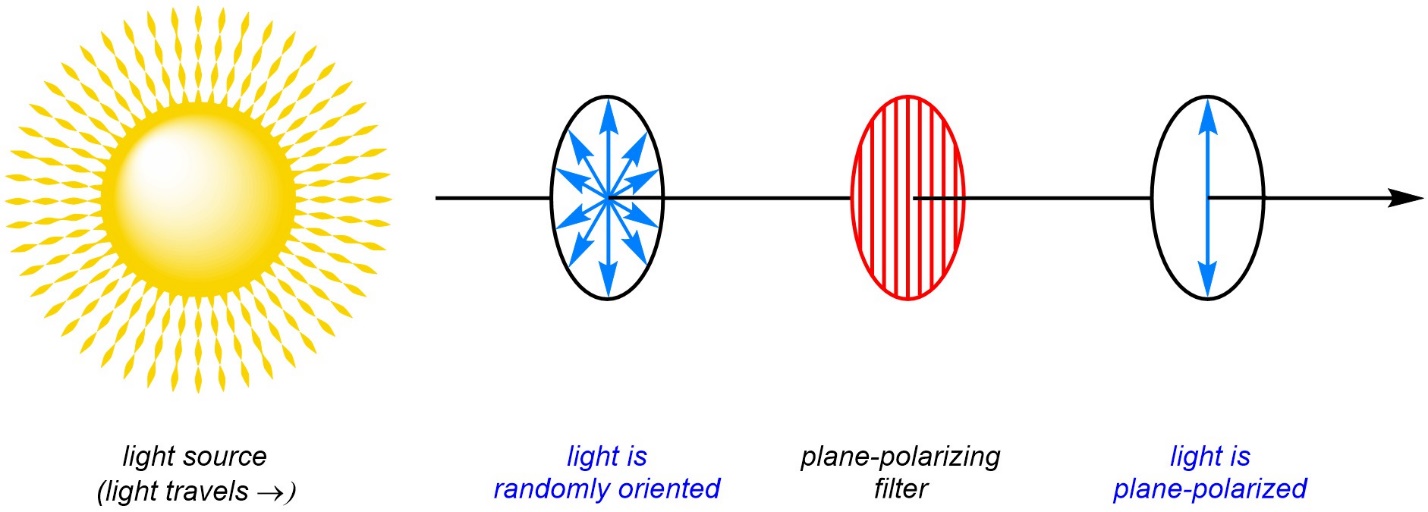
Figure 4.41 – Plane-Polarization of Light Using a Filter.
Enantiomers interact with polarized light differently. More specifically, the plane is rotated by each enantiomer by the same amount (magnitude) but in opposite directions. Understanding exactly how this happens requires significantly more background information on the physics of light and is well beyond the scope of this text. Since light is being rotated by the interaction, this effect is called optical rotation.
After polarizing the light, a sample of a chiral compound can be placed in the path of the light. Then, as the light travels through the sample its plane will be rotated either clockwise or counter-clockwise depending on which enantiomer is in the sample (Figure 4.42). The direction and degree to which the plane is rotated can be measured and used to determine which enantiomer the sample was.
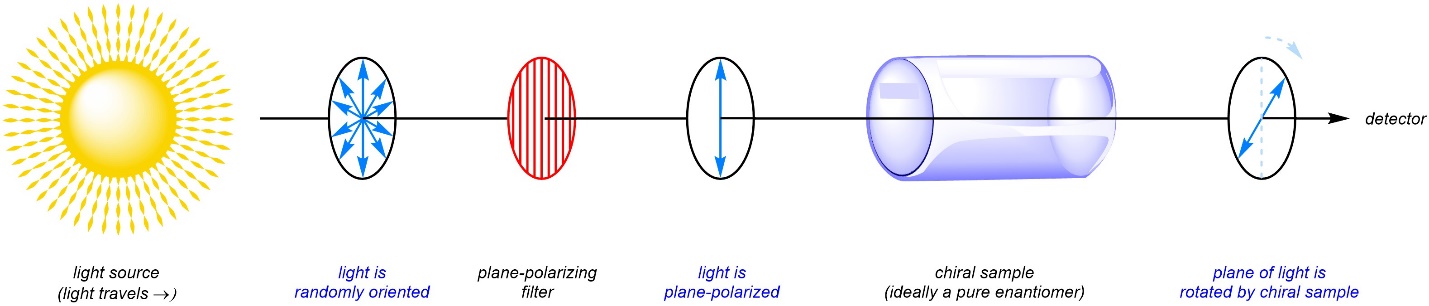
Figure 4.42 – Rotation of Plane-Polarized Light by a Chiral Sample.
4.7.2. Classifying Enantiomers by Optical Rotation
There are other ways of determining which enantiomer of a compound a sample is. When a very pure sample of one enantiomer is found the optical rotation can be measured. This gives a reference for the magnitude and direction that the light should be rotated by a “pure” enantiomer. The magnitude can vary significantly depending on the exact molecular structure. However, for all compounds one enantiomer will rotate the plane clockwise, and the other enantiomer will rotate the plane counter-clockwise.
Because enantiomers rotate the plane in opposite directions, they can be classified by which way they rotate it (Figure 4.43). The enantiomer that rotates light clockwise is called dextrorotary. This is indicated using a small italic “+” or “d” in brackets before the compound’s name. The enantiomer that rotates light counter-clockwise is called levorotary. This is indicated using a small italic “–” or “l” in brackets before the compound’s name.

Figure 4.43 – Dextrorotary vs. Levorotary.
For those familiar with D/L nomenclature from bioorganic chemistry, it is important remember that these two systems are not related in any way.
Optical rotation is a physical property, like melting/boiling point. There is no direct relationship between absolute configuration and being dextrorotary or levorotary (Figure 4.44). Compounds with many stereocentres that are chiral can have their enantiomers classified based on optical rotation. This means that there is no way to know any stereochemical information (absolute configurations) about a compound simply from knowing if it is dextrorotary or levorotary.
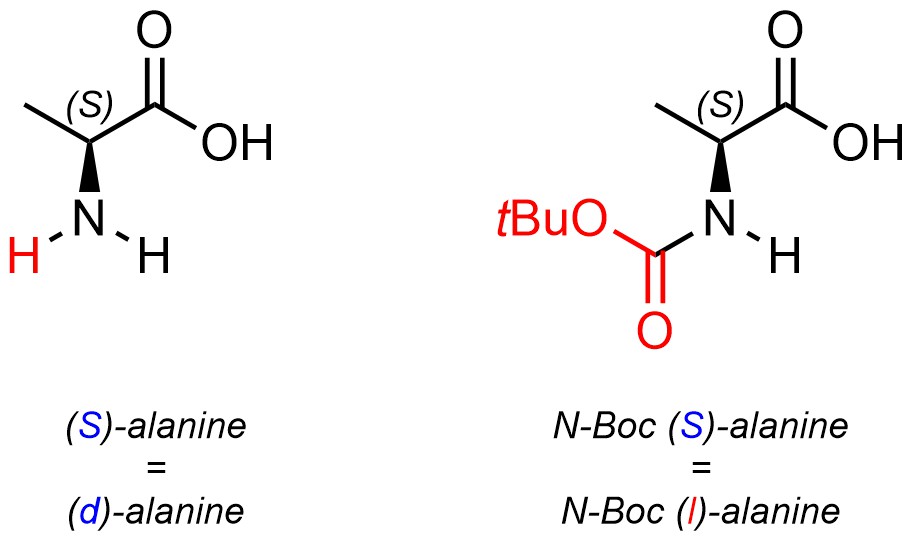
Figure 4.44 – Example Highlighting the Lack of Correlation Between Absolute Configuration and Optical Rotation.
A chiral compound can exist as several kinds of mixtures. If the mixture is made up by 50% of one enantiomer and 50% of the other enantiomer, the sample is said to be racemic (or is called a racemate). If the mixture is made up by any other ratio of the two enantiomers, the sample is said to be scalemic (or is called a scalemate). The terms scalemic and scalemate are not widely used, with most chemists preferring enantioenriched (the mixture is enriched with more of one enantiomer than the other). If there is only one of the two enantiomers, the sample is said to be enantiopure. This type of mixture is hypothetical, it is impossible to achieve in real life. It is possible that some natural products are produced enantiopure, but it is not possible to measure accurately enough to be certain. Unfortunately, many sources use this term (incorrectly) for high enantioenrichment (e.g. >99% of a sample is one enantiomer).
Racemates do not rotate plane-polarized light. For every molecule of one enantiomer, which rotates the plane in one direction, there is a molecule of the other enantiomer, which rotates it the other direction. The result is no net rotation. Racemates are very common in synthetic compounds, though some natural products are also produced as racemates.
Scalemates (enantioenriched mixtures) do rotate plane-polarized light. However, they will not rotate it to the same magnitude as the “enantiopure” sample. It is possible to use mathematical formulas and the magnitude that is rotated to determine the approximate ratio of the two enantiomers in a scalemate. The exact process and equations to do this are outside the scope of this text.
4.7.4. Enantiomeric Ratio vs. Enantiomeric Excess
There are two common systems for describing enantioenriched samples (scalemates).
The ideal system to describe a mixture of enantiomers is by using the enantiomeric ratio (er). This is a ratio of the percentages of each enantiomer (Figure 4.45). As such, the numbers should sum to 100. Simplifying the fraction is acceptable but not encouraged.
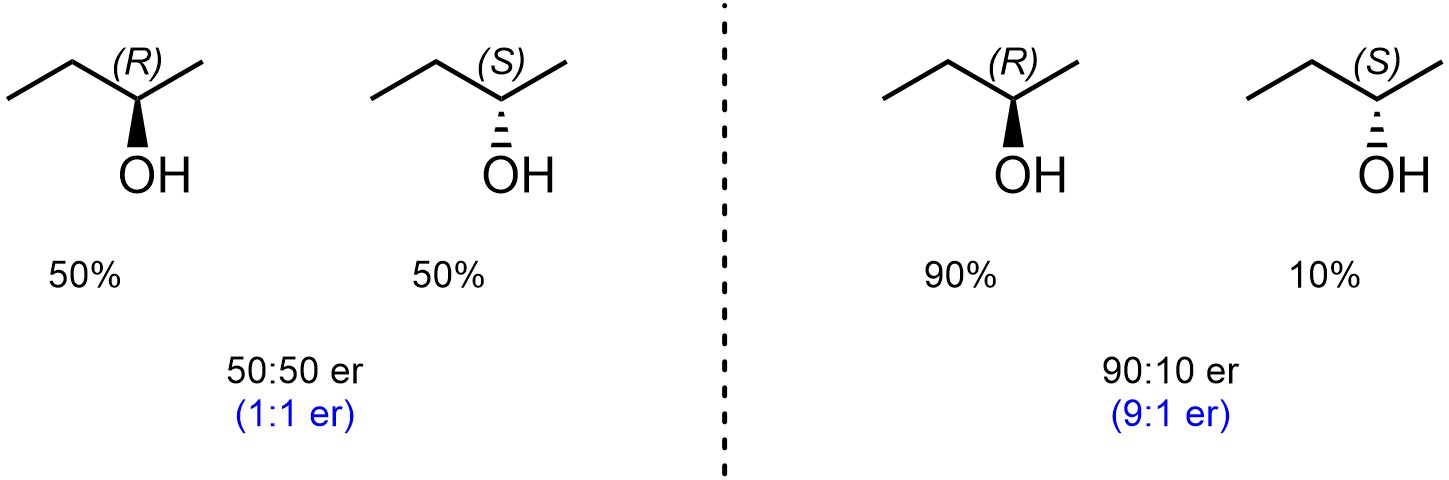
Figure 4.45 – Examples of Reporting Enantiomeric Ratio.
Unfortunately, the more common way to describe a mixture of enantiomers is by using the enantiomeric excess (% ee). This is a non-linear percentage calculated using the following formula:
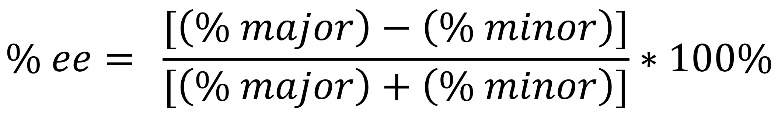
Use of the formula is not required in this text but seeing it will clarify how example numbers are derived (Figure 4.46).
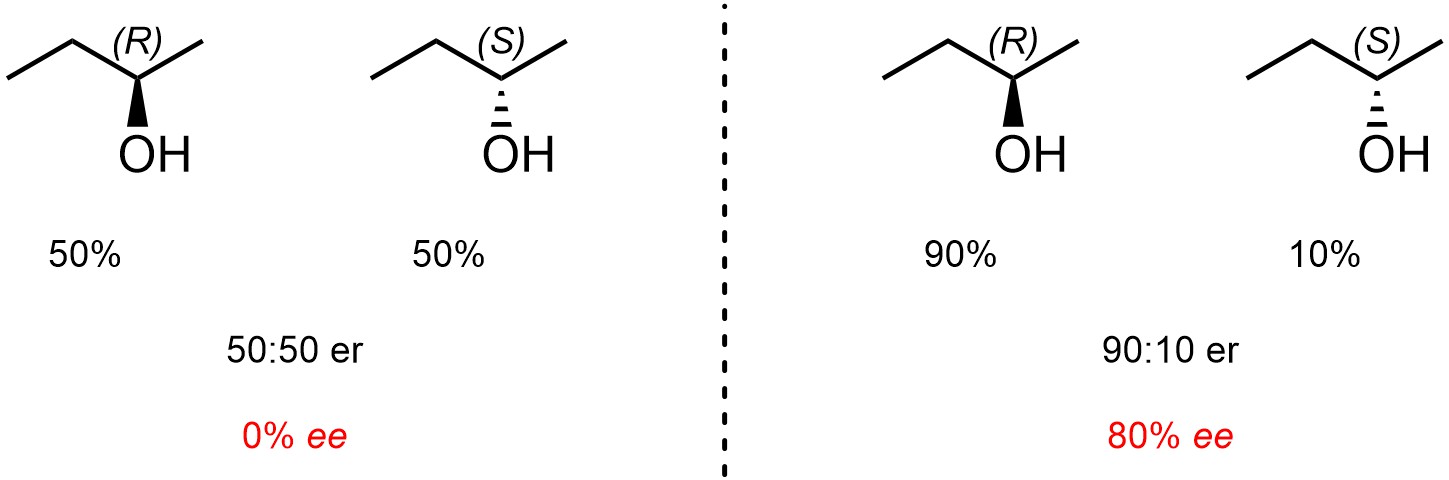
Figure 4.46 – Examples of Reporting Enantiomeric Excess Contrasted with Enantiomeric Ratio.
Enantiomeric excess (% ee) can alternatively be directly determined from the magnitude of optical rotation measured. As this was the primary way of determining the ratio of enantiomers for many years, it has become tradition to report the value using % ee. However, the use of % ee is heavily discouraged. Modern techniques directly measure the ratio of enantiomers, which may be recorded as enantiomeric ratios and are simpler to interpret. There are several other issues with the enantiomeric excess system, primarily related to parameters measured in Physical Chemistry.

