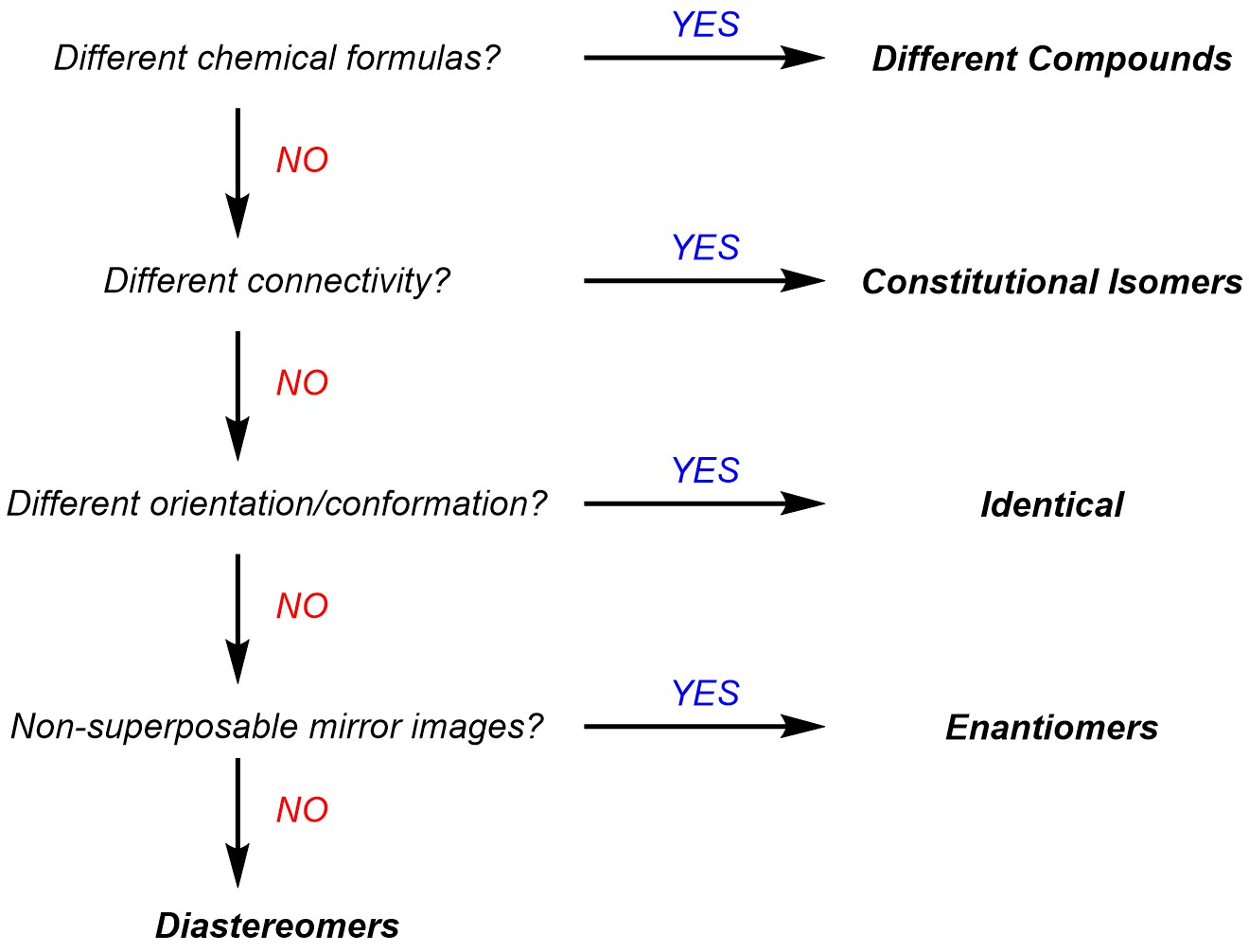
4.2. Classification of Isomers
Isomers are different molecules formed from the same set of atoms. There are several different ways this can be accomplished.
4.2.1. Constitutional Isomers vs. Stereoisomers
Consider the molecular formula C4H10O. Many different molecules can be generated using these atoms (Figure 4.1).
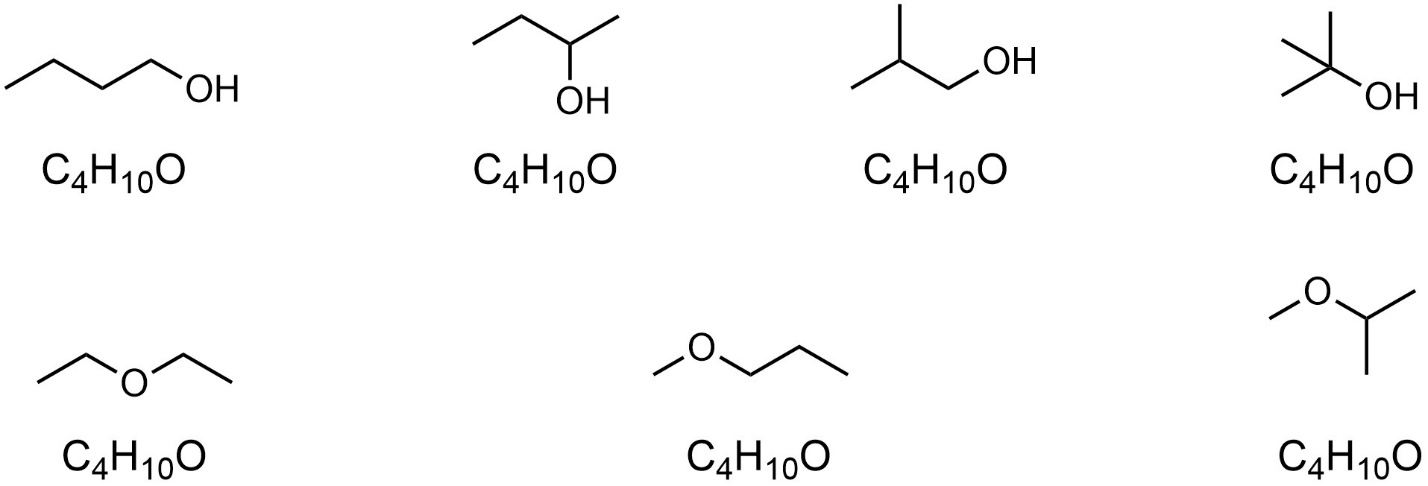
Figure 4.1 – Constitutional Isomers of the Formula C4H10O.
Molecules that have the same chemical formula BUT their atoms are connected in a different sequence are called constitutional isomers. The simplest way to recognize that a pair of molecules are constitutional isomers is if they have different connectivity. Alternatively, the two will have the same atoms (molecular formula) but have completely different names under the IUPAC system (Figure 4.2). Even if you cannot generate the full name yourself, if a cursory inspection suggests they will have different names they are almost certainly constitutional isomers.
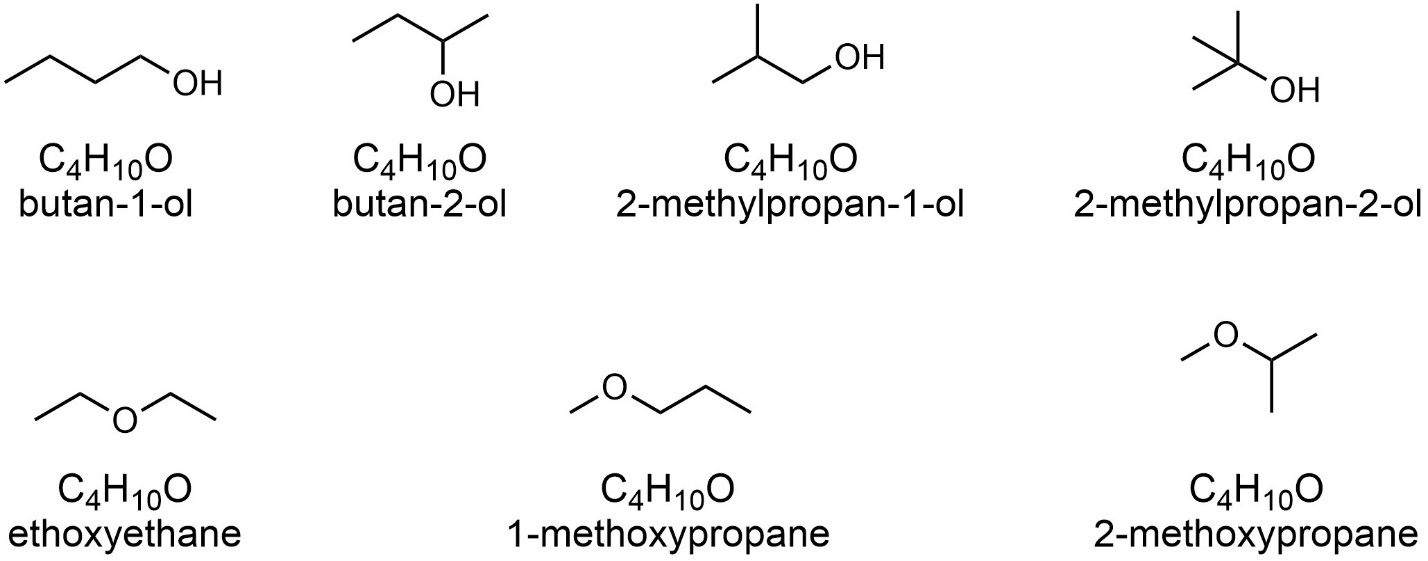
Figure 4.2 – Named Constitutional Isomers of the Formula C4H10O.
If the depiction of one of these molecules becomes more precise and includes three-dimensional information (Figure 4.3) then the situation becomes more complex. Consider the relationship between the left and right molecules. They have the same connectivity, but they are still different.
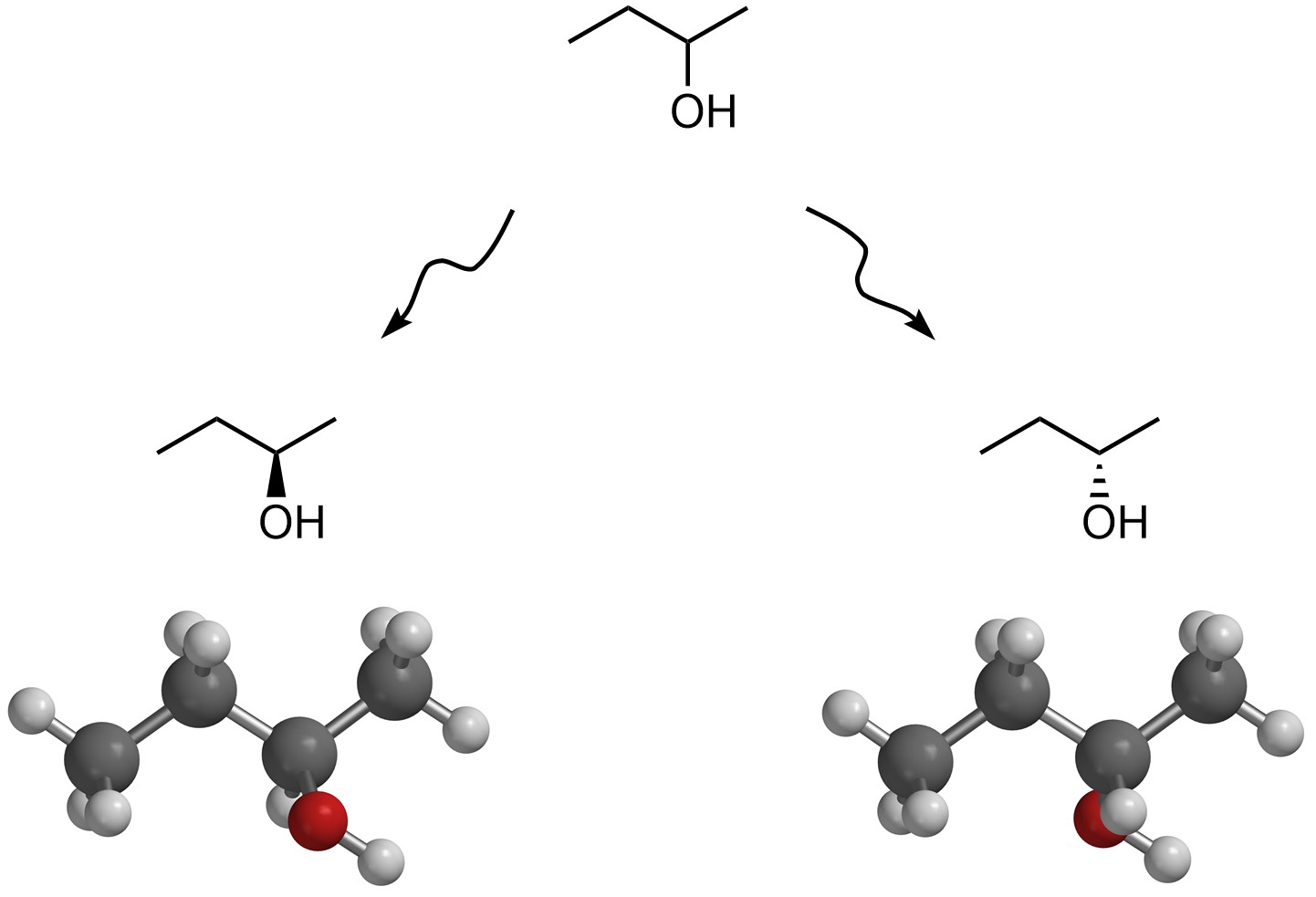
Figure 4.3 – Stereoisomers of Butan-2-ol.
Molecules that have the same chemical formula AND their atoms are connected in the same sequence BUT they differ in the three-dimensional arrangement of those atoms are called stereoisomers. The rest of this chapter will deal with these kinds of isomers.
4.2.1.1. Conformation vs. Configuration
Technically, under the definition of stereoisomers (see Section 4.2.1.) conformations are a type of stereoisomer. They have the same formula, their atoms are connected in the same sequence, and they have different three-dimensional arrangements of their atoms. So-called conformational isomers are interconvertible by rotations around single bonds. However, this is not always obvious given the tenuous distinction between some single and double bonds (see Section 5.5). Additionally, conformations typically interconvert rapidly at room temperature. As a result, in this text we will not consider conformational isomers to be relevant as stereoisomers; a pair of conformations are considered different representations of the same molecule (i.e. the relationship between them is “identical compounds”; Figure 4.4)). Remember also that the same molecule can be represented in several orientations; all of these are depictions of the exact same molecule.
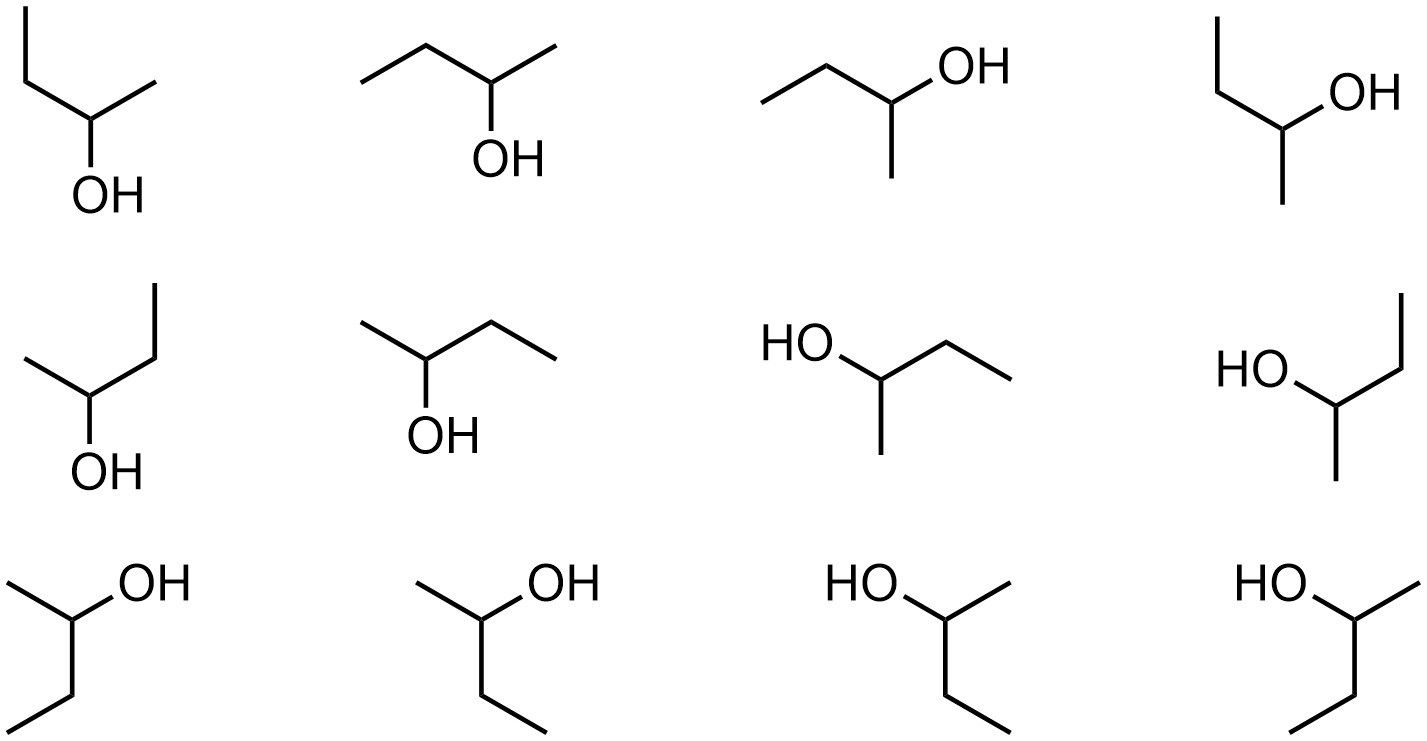
Figure 4.4 – Conformations and Rotations of Butan-2-ol.
Compare the two molecules above again (Figure 4.3). It is not possible to simply rotate single bonds and turn the molecule on the left into the molecule on the right. These two molecules are not different conformations of each other. In fact, the only way to interconvert the two would be to break bonds and reattach the atoms in a different way. We refer to the three-dimensional arrangement of bonds around a central atom that connect to the other atoms as the central atom’s configuration.
The difference between conformation and configuration is very important. Conformations are temporary “poses” that a molecule can adopt. The configuration of a molecule is permanent and can only change by breaking bonds and reattaching the atoms differently. This is also true at the macro level. When you go from sitting to standing you rotate parts of your body and change your pose (your conformation). In order to change your configuration, you would need to detach two of your limbs and reattach them elsewhere, such as sewing your dismembered leg to your shoulder and your arm to your waist. This example is slightly macabre but should reinforce the idea that despite their similar sounding names, conformation and configuration are not related concepts.
4.2.2. Stereoisomers – Enantiomers
Stereoisomers can be subdivided into two main categories.
Enantiomers are a pair of stereoisomers that are non-superposable mirror images of each other. That is, the mirror image of the molecule cannot be rotated around and perfectly overlapped with the original. The two stereoisomers of butan-2-ol above are enantiomers (Figure 4.5).
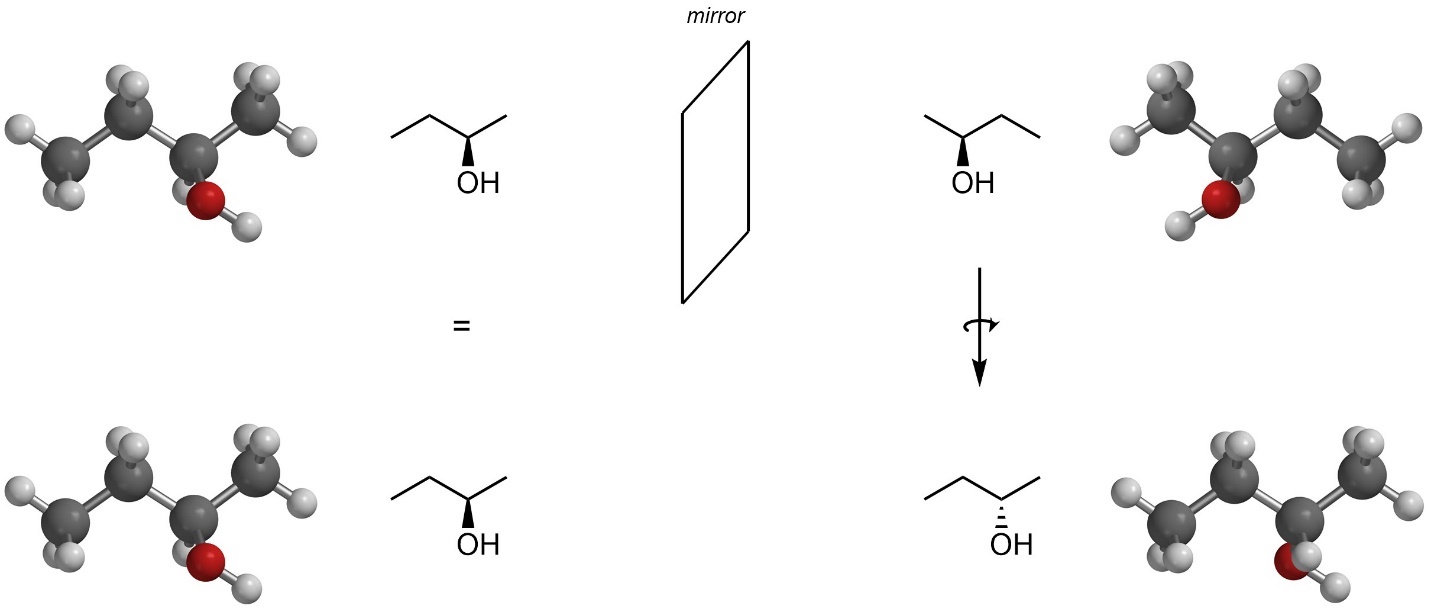
Figure 4.5 – Enantiomer Relationship of Stereoisomers of Butan-2-ol.
Although the definition of enantiomers seems incredibly specific, enantiomers come up very frequently in nature and have a special relationship with each other (see Section 4.5.).
Imagine a (perfect) ball held in front of a mirror (Figure 4.6). If you could take the mirror image and overlap it onto the original ball they would coincide exactly. This is called being superposable. In other words, the ball and its mirror image are identical.
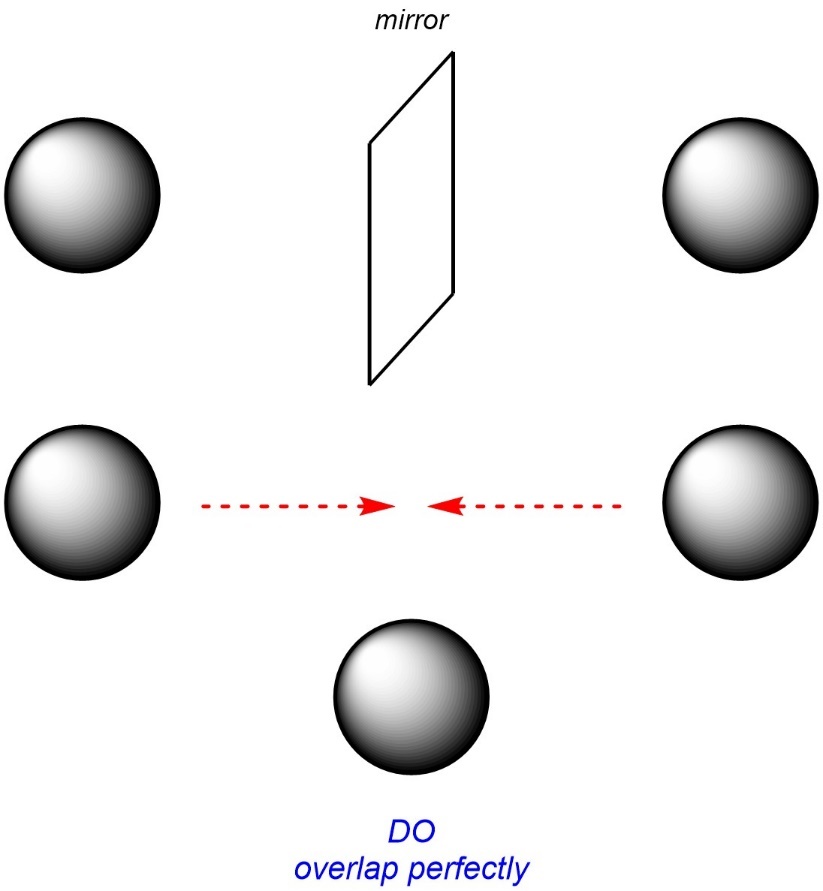
Figure 4.6 – Overlapping a Ball and its Mirror Image.
Imagine your right hand held in front of a mirror (Figure 4.7). If you could take the mirror image and overlap it onto the original hand they would NOT coincide exactly. This is called being non-superposable. In other words, the hand and its mirror image are different.
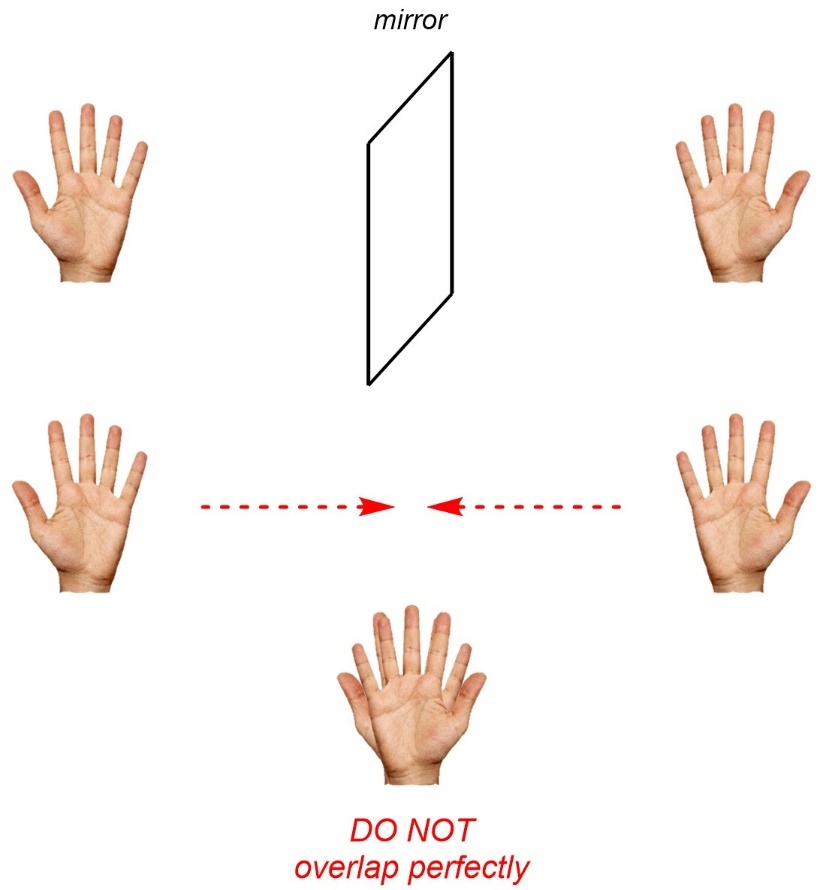
Figure 4.7 – Overlapping a Right Hand and its Mirror Image.
The ability of objects to exist as non-superposable mirror images of each other is called chirality. In the previous examples, we would say that the ball is achiral (its mirror image is superposable on itself; its mirror image is identical to the original). Conversely, we would say that your right hand is chiral (its mirror image is NOT superposable on itself; its mirror image is different from the original).
The exact same principle can also be applied to molecules. For example, butan-2-ol above is chiral, while butan-1-ol is achiral (Figure 4.8)
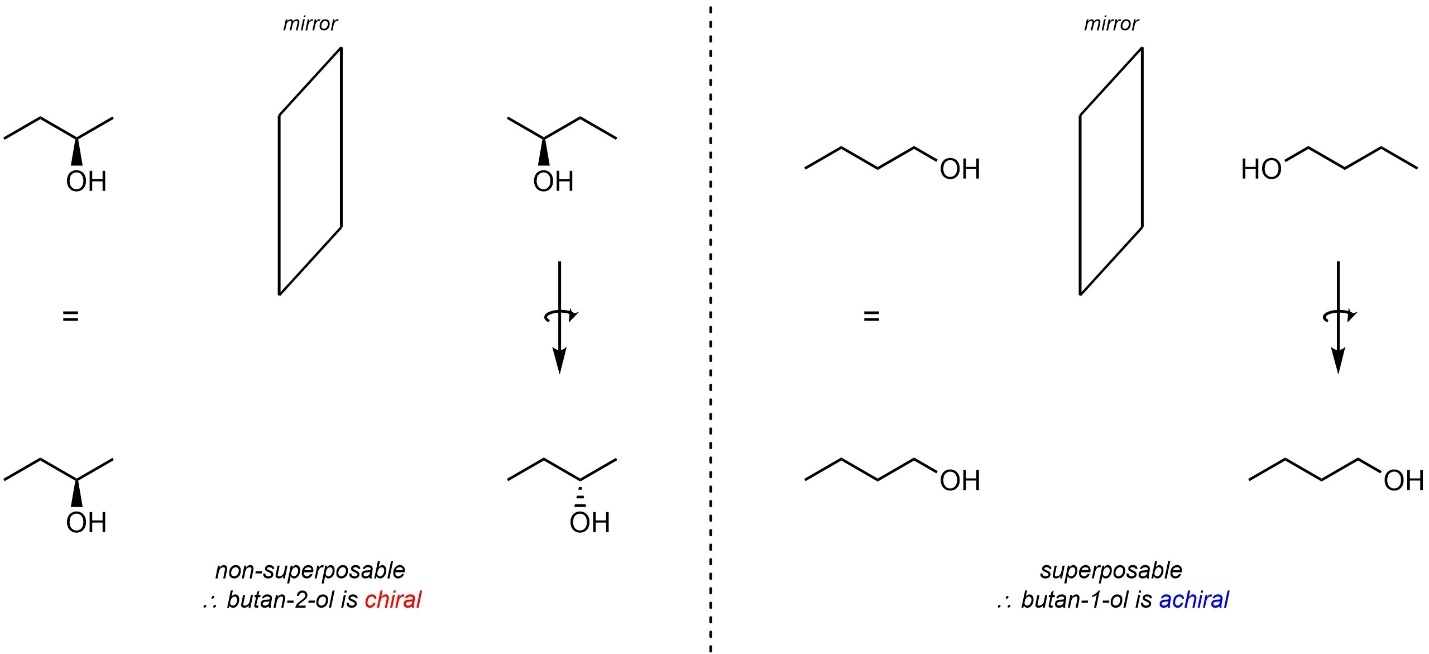
Figure 4.8 – Chiral Butan-2-ol vs. Achiral Butan-1-ol.
4.2.2.2 How to Determine if Something is Chiral or Achiral
The only way to be absolutely confident that a molecule is chiral or achiral is to build a model of (or draw) the two mirror images and compare them. While comparing molecules you are allowed to rotate them (as in Figure 4.8) and you are allowed to change their conformation. The only restriction is that you cannot break bonds. While the resulting mirror images can always be compared, sometimes rotating the molecule or changing its conformation before creating the mirror image helps make the comparison easier (Figure 4.9).
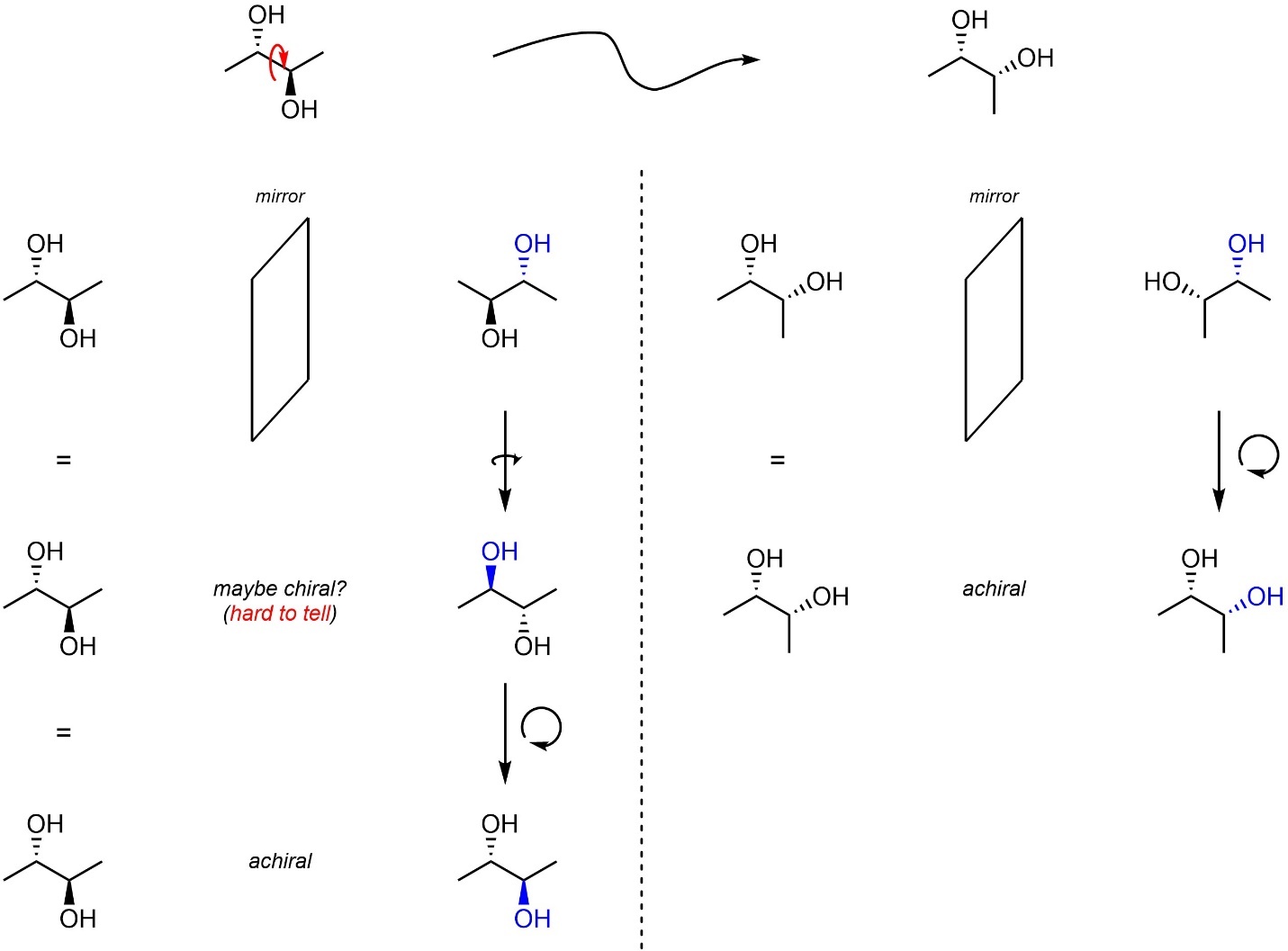
Figure 4.9 – Example of Simplifying Comparison of Mirror Images by Changing the Conformation.
Sometimes there is a useful shortcut. If the molecule contains an internal plane of symmetry (a mirror plane within the molecule), then it can immediately be classified as achiral (Figure 4.10). The left and right sides of these molecules are mirror images of each other in this orientation. Again, rotations and conformation changes are allowed while searching for internal planes of symmetry. Remember that conformation is changeable but still exists. For example, the stereoisomer of 1,4-dimethylcyclohexane is in a chair conformation, not the imaginary planar conformation. The two-dimensional drawing of this molecule appears to have two internal mirror planes, but the three-dimensional conformation has only one. In other words, molecules must be visualized and analyzed in their three-dimensional conformations to be accurately assessed.
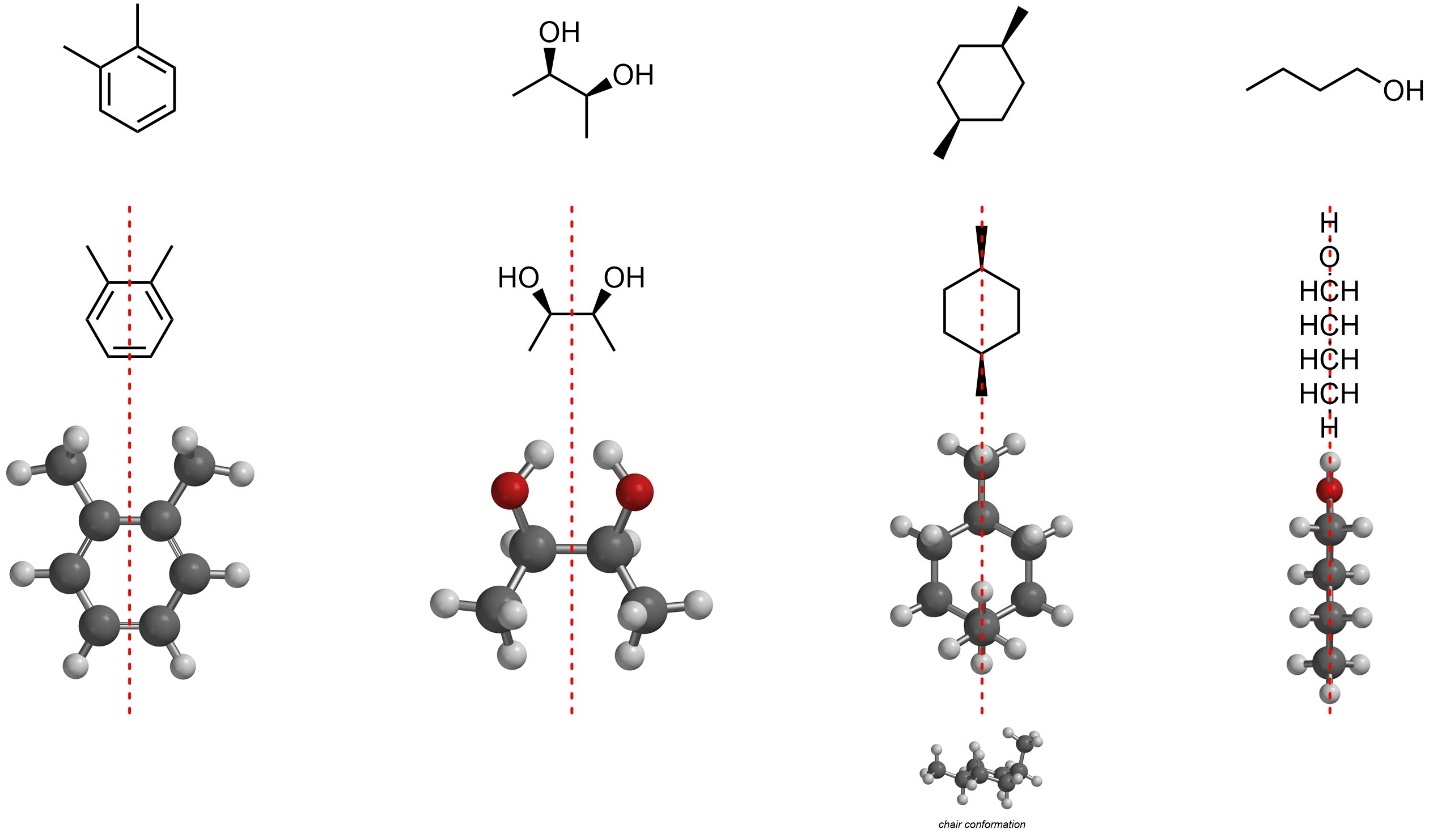
Figure 4.10 – Examples of Finding Internal Mirror Planes in Achiral Molecules.
It is important to remember that this is a shortcut, not the formal way of classifying chiral and achiral. For example, finding an internal mirror plane immediately means the molecule is achiral. Not finding an internal mirror plane does not necessarily mean the molecule is chiral. It could simply be that the plane is hard to find. In rare cases, some molecules do not have an internal plane of symmetry but are still achiral. Examples of these will not feature in this text, but this highlights the need to use a more formal approach when an internal mirror plane is not found.
4.2.2.3 Chirality vs. Stereogenicity
Terminology for stereochemistry was first created before a thorough understanding of exactly what was being discussed developed. This has largely been resolved in recent years. Most of the issues were fixed by establishing a better definition of stereogenic centres (often stereocentres). An atom is a stereogenic centre if the interchange of two of its substituents can produce a new stereoisomer; the centre ‘‘generates’’ stereochemistry.
Stereogenic Centre (or Stereocentre): A grouping of atoms consisting of a central atom and distinguishable [substituents], such that the interchange of any two of the substituents leads to a stereoisomer.
IUPAC Gold Book: Basic Terminology of Stereochemistry
PAC, 1996, 68, 2193 (page 2219)
The carbon atom bonded to oxygen in butan-2-ol is stereogenic (Figure 4.11). Interchanging two of its substituents in the left isomer generates a different stereoisomer.
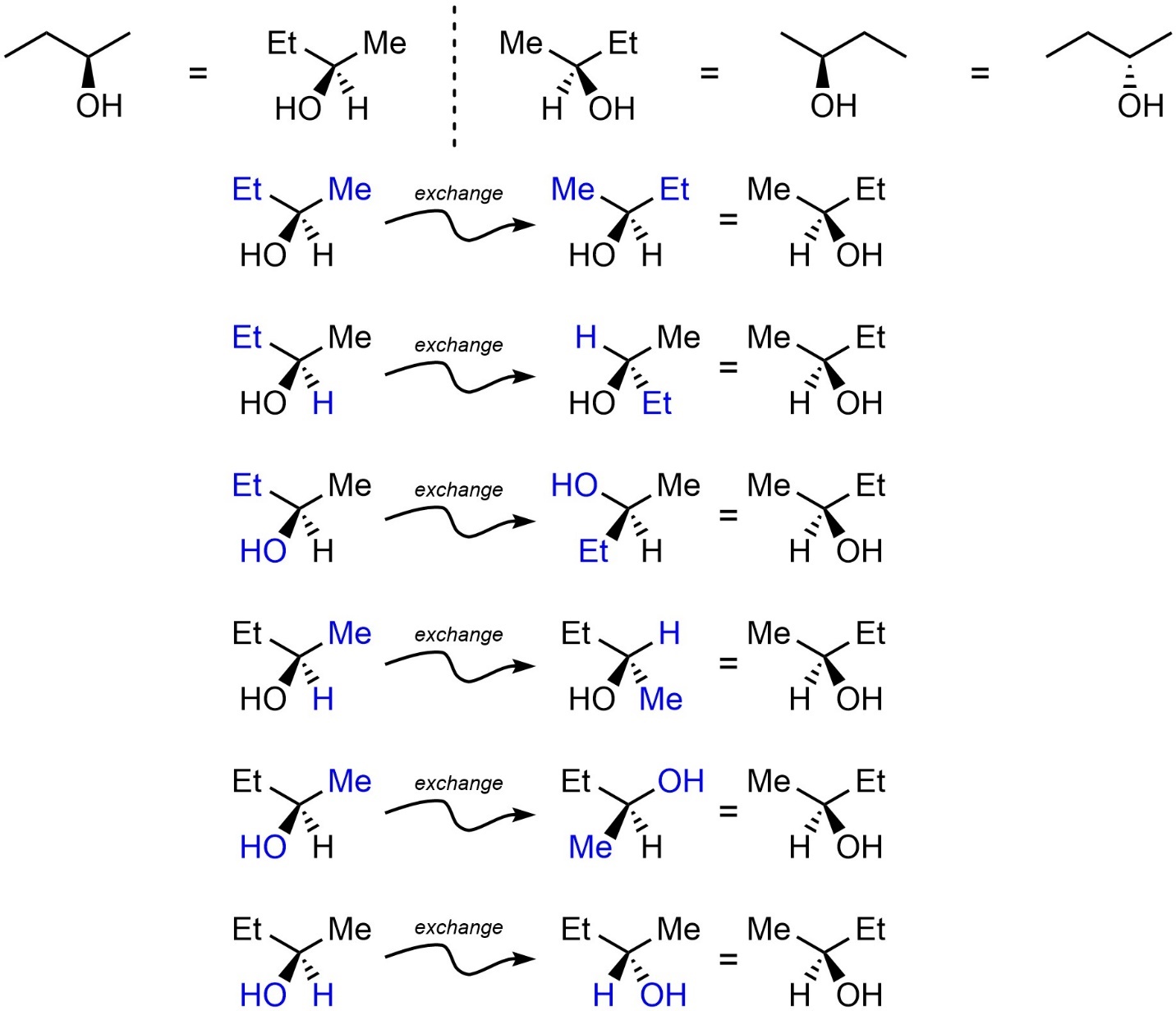
Figure 4.11 – Highlighting the Stereocentre of Butan-2-ol.
Older texts and sources sometimes use the terms “chiral centre”, “chiral atom”, “chiral carbon”, “asymmetric centre”, or “asymmetric carbon” as synonyms for stereocentre. The use of these terms is heavily discouraged. Chirality and stereogenicity (stereocentres) are distinct concepts and are not related. Molecules can be chiral without having stereocentres. Molecules can have stereocentres but not be chiral. Moreover, stereocentres are not required to be carbon atoms (see Section 4.3).
A quick example can reinforce the distinction. Recall that chirality is the ability of objects to exist as non-superposable mirror images. That means that chirality is a property of the entire object. For example, a dismembered hand and a snail shell are chiral (Figure 4.12). There is no “stereocentre” in either object.

Figure 4.12 – Macroscopic Examples of Chirality Without Stereogenic Centres.
There are other types of stereogenicity that do not require a specific centre/atom be stereogenic. Most commonly these are referred to as stereogenic units (sometimes called stereogenic elements). Unfortunately, there is still controversy in accurately defining and naming these types of units. For the purposes of this text these terms will be avoided, but it is important to recognize that stereogenicity can be more complex than outlined above.
4.2.2.4 CIP Nomenclature and Absolute Configuration
Accurate communication again requires that there be a distinction in the names of stereoisomers. Because the configuration is what is being described, the naming of stereocentres is referred to as their absolute configuration. The absolute configuration describes the exact three-dimensional arrangement of atoms around the stereocentre. For example, the two stereoisomers of butan-2-ol are properly called (R)-butan-2-ol and (S)-butan-2-ol (Figure 4.13).
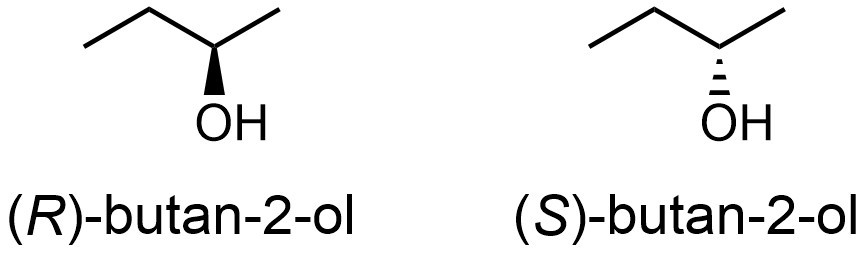
Figure 4.13 – Absolute Configuration of the Stereoisomers of Butan-2-ol.
The system of rules for determining the absolute configuration of the stereocentre is called the Cahn-Ingold-Prelog (CIP) system. Most stereocentres encountered in this text may be classified as R or S (these labels generally apply to stereocentres with four substituents). The rules for differentiating these can be broadly summarized as: assigning priority to the substituents (based on atomic number), orienting the molecule using the lowest priority group (so that all “viewers” see the same perspective), and determining whether the priority of the remaining substituents descends in a clockwise or counter-clockwise fashion.
The ability to rapidly assign absolute configuration is essential to organic chemistry and generally requires a great deal of practice to be done efficiently and reliably.
4.2.2.5 How to Assign R/S Configurations
The systematic way of assigning absolute configuration is straightforward but can be tedious when many stereocentres are present. With practice the process can usually be streamlined, and an absolute configuration assigned in a few seconds per stereocentre.
Determine which atoms are stereocentres. This step is often slow for beginners but becomes straightforward with practice.

Draw in implied hydrogens for stereocentres. This step is optional but is particularly helpful for introductory students.
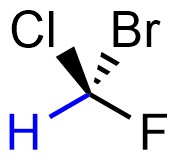
Assign priority to each group. Priority is based on atomic number. The highest priority group is assigned as 1, then 2, then 3, and finally 4 for the lowest.
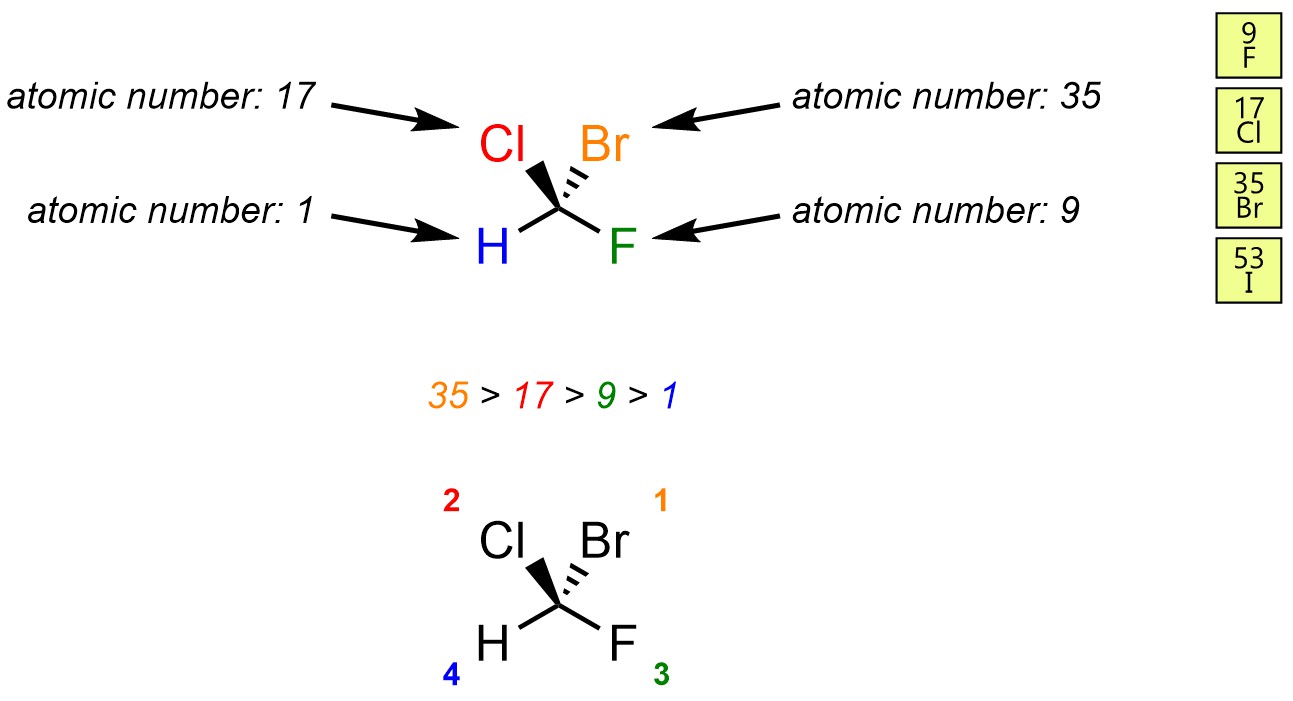
Reorient the molecule so that the priority 4 group is facing away from the viewer. This step is not optional. Without this step, any assignment is equivalent to a random guess.
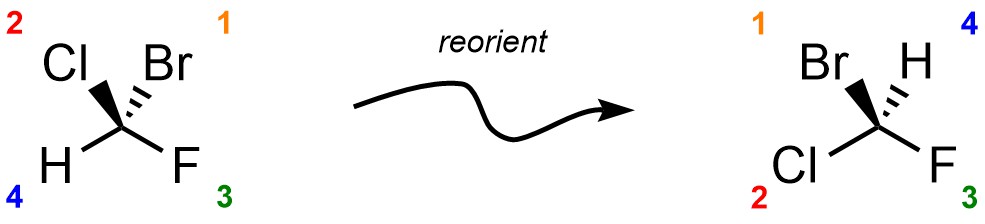
Draw a circular arrow from Priority 1 to Priority 2 to Priority 3. If the arrow proceeds clockwise, the absolute configuration is R. If the circle proceeds counter-clockwise, the absolute configuration is S.
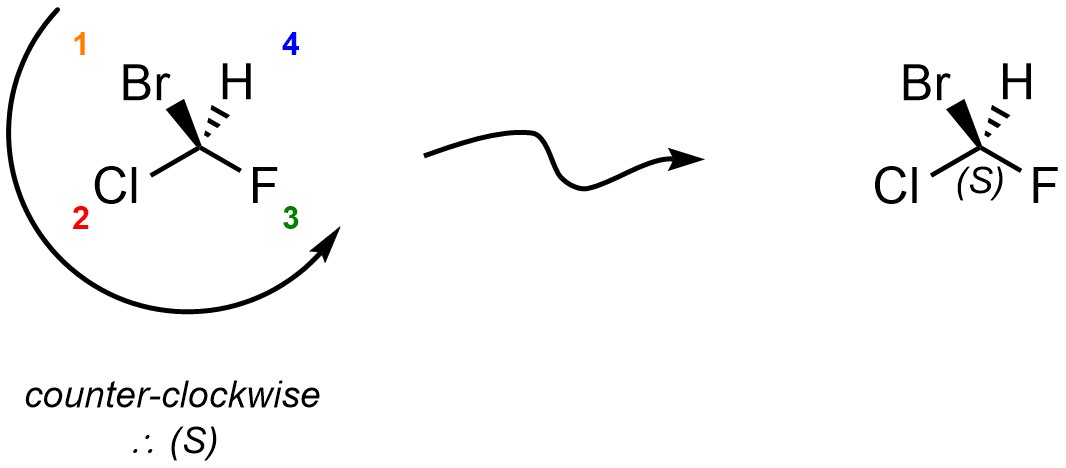
Reorienting the molecule is required to ensure that the relative descriptors “clockwise” and “counter-clockwise” are applied from the same perspective each time. For instance, there are 12 different orientations the example molecule may be viewed from. Of those, six lead to the correct assignment, and six lead to the incorrect assignment. By coincidence the orientations with H being to the left are the three that also lead to the correct assignment for this molecule, but this is only coincidental and is not generally true.
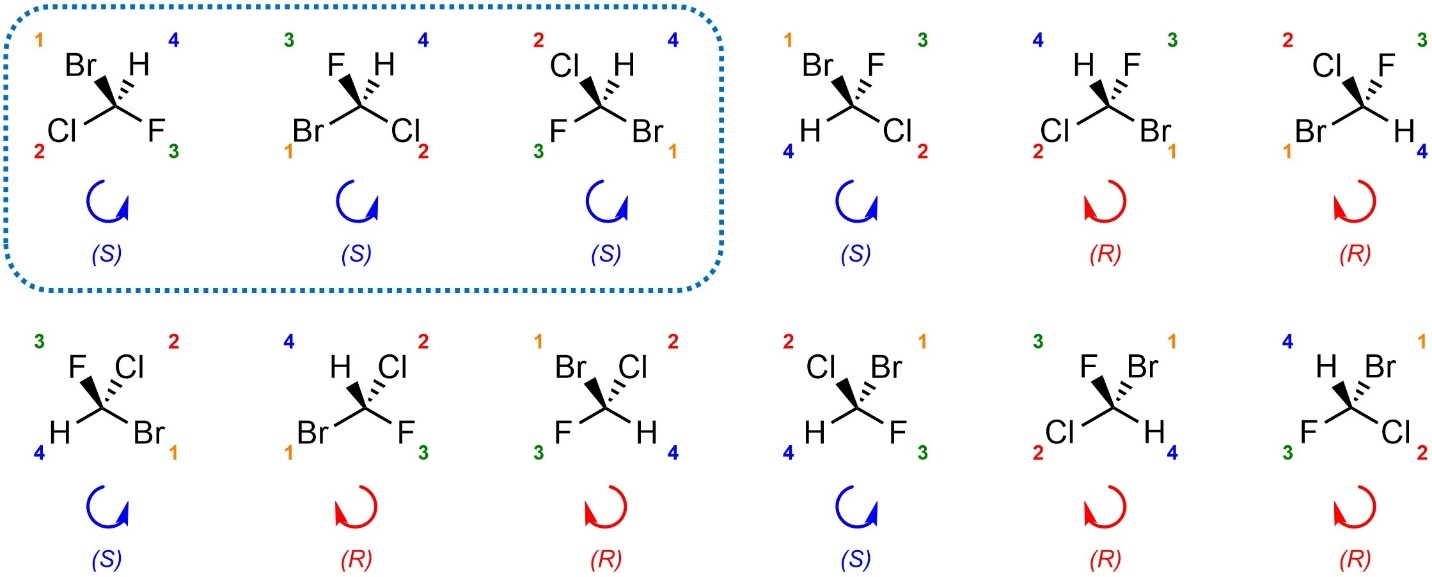
Re-drawing each stereocentre each time can be time consuming. There are two alternatives to avoid it.
Visualizing and rotating a three-dimensional model of the molecule internally (in your mind’s eye) is a valid approach. With enough practice some people become good at doing all five steps “in their head”. However, this approach does not work for everyone; some people can do it innately, but most require dozens or even hundreds of practice examples worked through to develop the skill. Even among those able to do it, mistakes are possible.
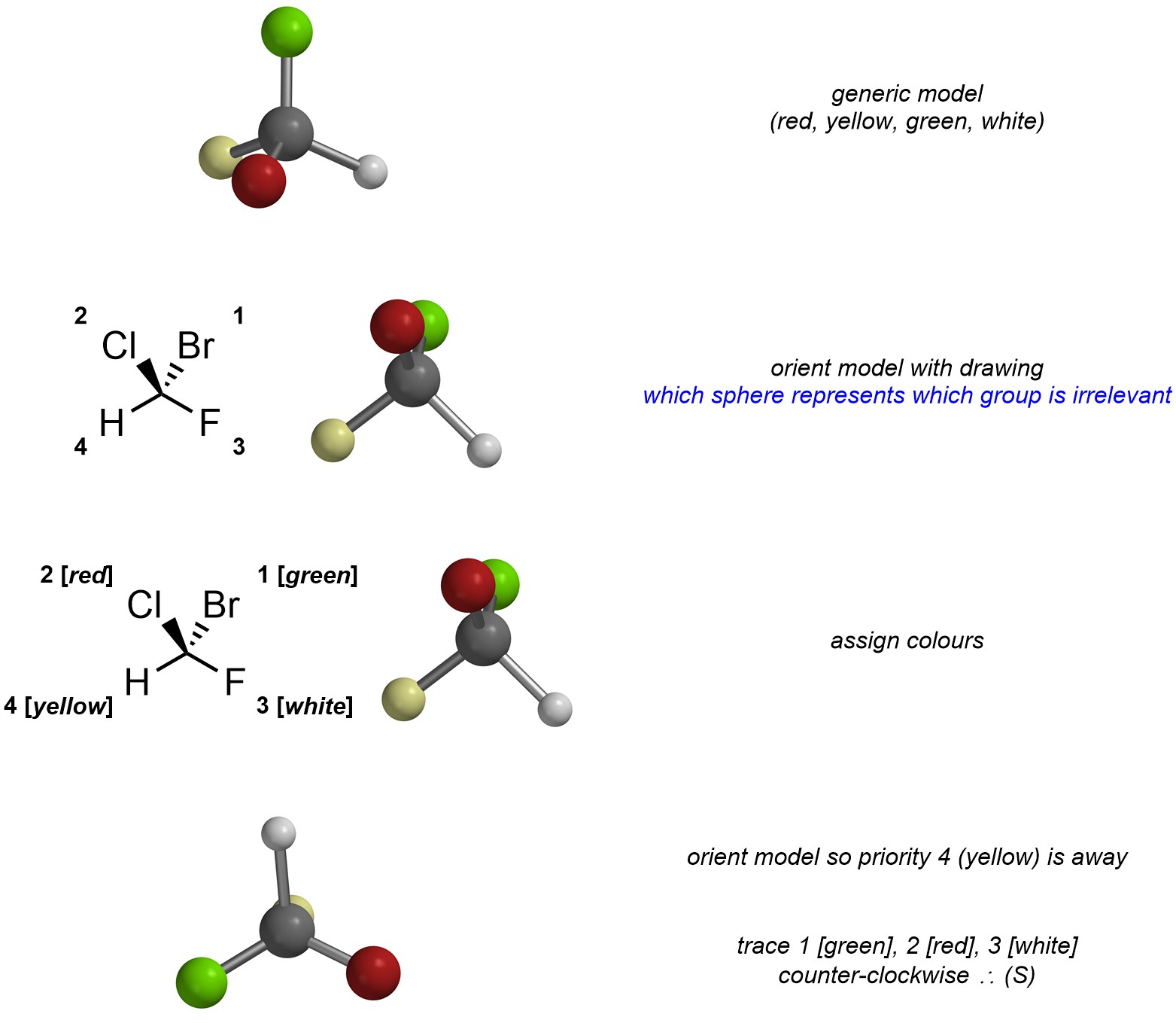
A more common approach is to build a generic molecular model of a stereocentre using a model kit. The model can be re-used for any stereocentre with the same number of substituents. When assigning priority (step 3), a colour is also assigned to the group. Then the physical model can be rotated freely to save having to re-draw the centre.
Some texts suggest a so-called “double exchange” approach. While a valid alternative method, the extra steps can lead to mistaken assignments. As such the use of this method is encouraged only if the reader is already familiar with it.
A variety of “tricks” can be found in other, typically online, sources. While these can be useful, generally the use of these “shortcuts” works only for some stereocentres and can lead to errors, especially with complex systems. As such their use is heavily discouraged.
Often stereocentres will have two or more connected atoms with the same atomic number. For example, the isomer of butan-2-ol below has a stereocentre at the carbon bonded to the oxygen (Figure 4.14). It is directly connected to a hydrogen (H; atomic number = 1), an oxygen (O; atomic number = 8), and two carbons (C; atomic number = 6). The hydrogen group is obviously priority 4. The oxygen group is obviously priority 1. However, it is not possible with just that comparison to determine which carbon-containing group is priority 2 and which is priority 3.
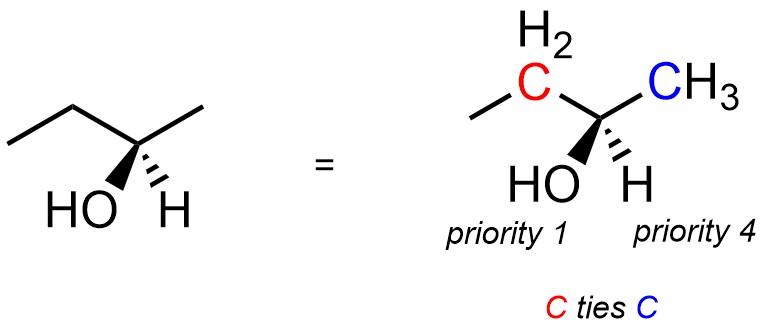
Figure 4.14 – First Attempt at Assigning Absolute Configuration to a Stereoisomer of Butan-2-ol.
In these cases the atoms attached to those atoms are next compared. The atoms are arranged in descending order of atomic number for each side and at the first discrepancy the higher atomic numbered side becomes the higher priority group (Figure 4.15).
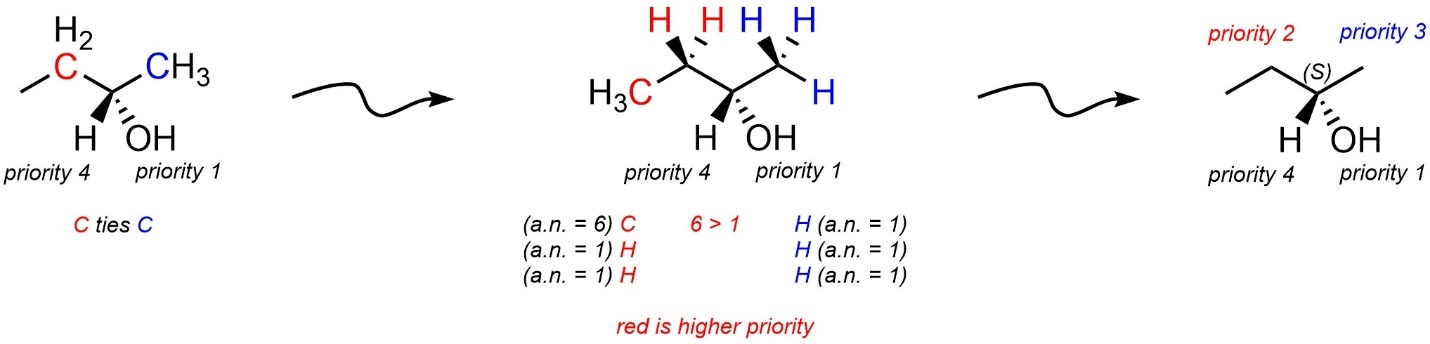
Figure 4.15 – Assigning Absolute Configuration to a Stereoisomer of Butan-2-ol.
If there is still a tie, continue moving down the chain (Figure 4.16). When there is complex branching this step can become complicated. Molecules with ambiguity for this will be avoided in this text.
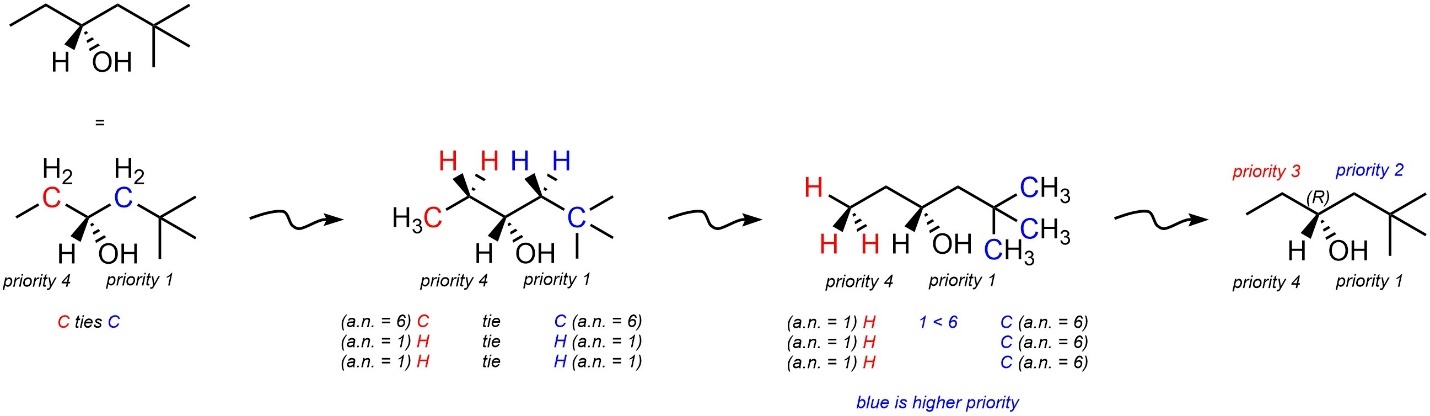
Figure 4.16 – Assigning Absolute Configuration to a Stereoisomer of 5,5-Dimethylhexan-3-ol.
It is important to remember to assign priority as soon as there is a difference in atomic numbers (Figure 4.17). For example, iodine beats bromine in the molecule below, so its group becomes priority 2 and bromine’s becomes priority 3. All further discrepancies are irrelevant. In this case, that the other two hydrogens ‘lose’ to the next two bromines is irrelevant.
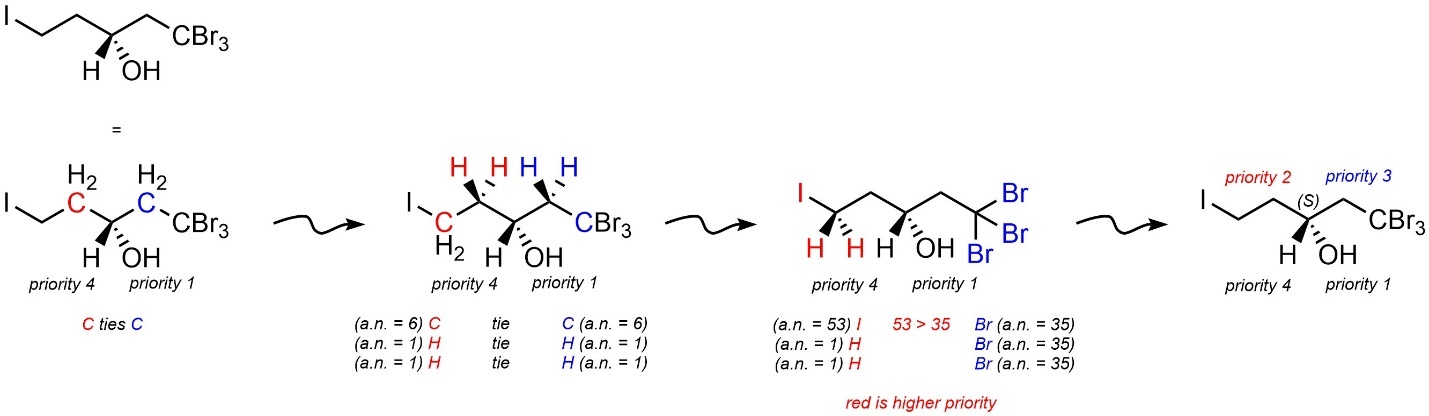
Figure 4.17 – Assigning Absolute Configuration to a Stereoisomer of 1,1,1-Tribromo-5-iodopentan-3-ol.
In the event that there are π bonds to consider, simply count each bond as being another instance of the same atom (Figure 4.18). Some texts recommend re-drawing the structure using so-called dummy atoms (sometimes called phantom atoms). This can be helpful in some instances, especially with certain alkenes, but significantly lengthens the time needed to assign the absolute configuration. As such the use of this method is encouraged only if the reader is already familiar with it.
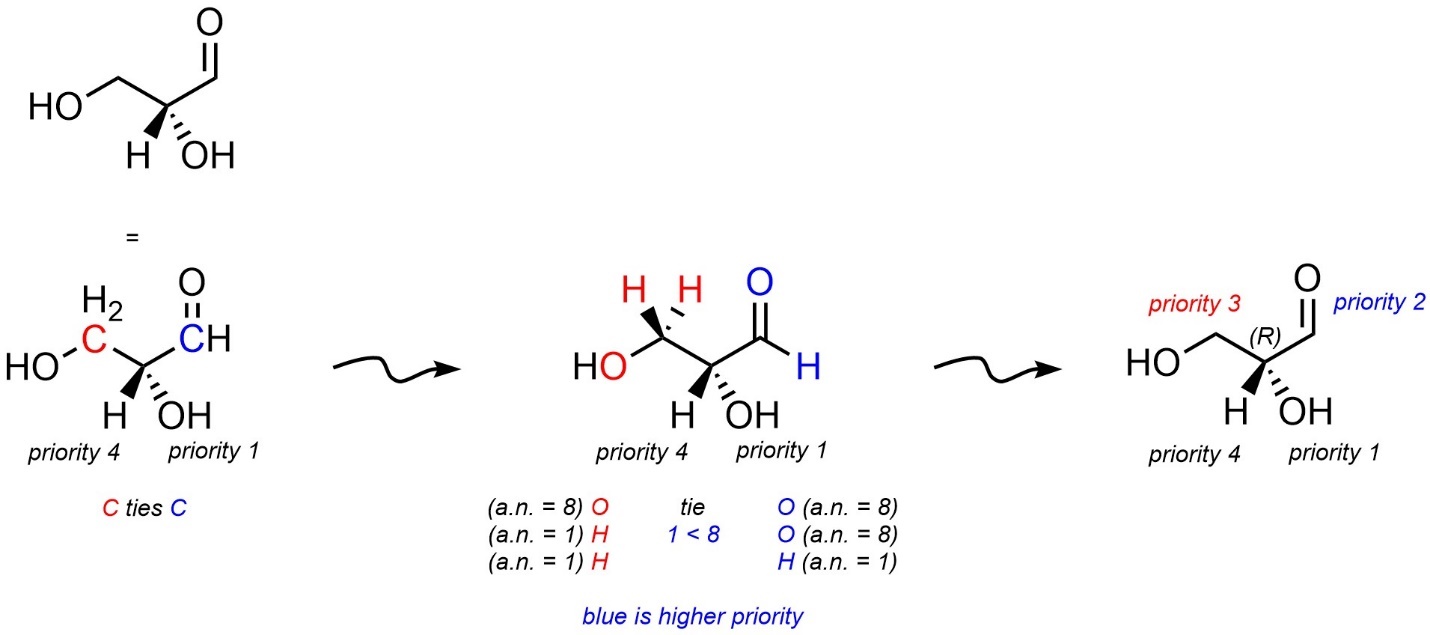
Figure 4.18 – Assigning Absolute Configuration to a Stereoisomer of 2,3-Dihydroxypropanal.
4.2.2.7 How to Draw a Compound’s Enantiomer
There are two approaches for drawing the enantiomer of a compound. Remember that in order to exists as a pair of enantiomers a molecule must be chiral (see Section 4.2.2).
Because a molecule’s enantiomer is the non-superposable mirror image the enantiomer can be drawn directly by mirroring it. Some students struggle to visualize a mirrored object. A helpful tool is to relate the position of the atoms and groups to the mirror itself (Figure 4.19). You may also use a small physical mirror while practicing to assist with the technique.
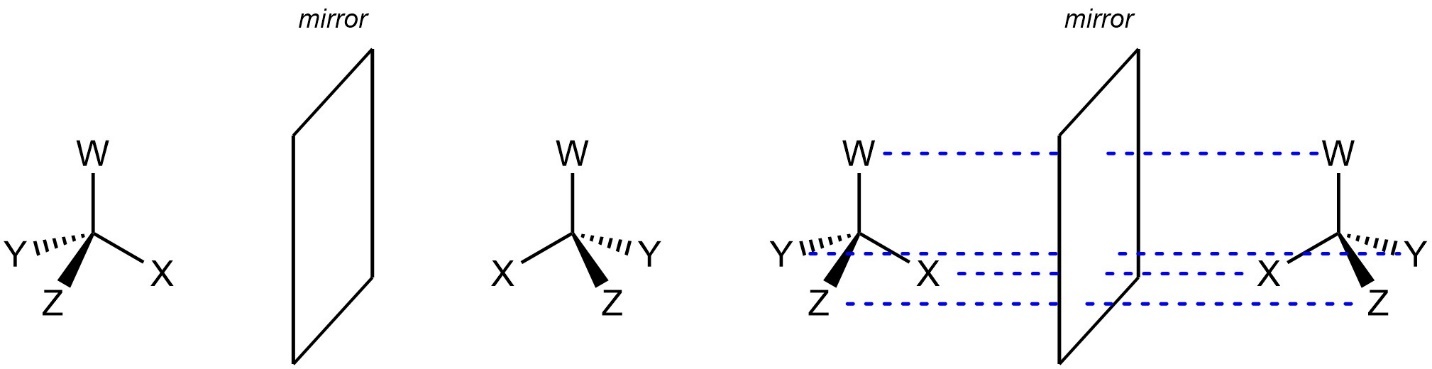
Figure 4.19 – Relating the Relative Positions of Atoms and Groups to the Mirror When Generating Enantiomers.
First, generate the exact mirror image of the molecule. Technically this is the enantiomer and can be left in this orientation. Normally it is good practice to rotate the new molecule around so that the two have their ‘skeletons’ aligned (Figure 4.20).
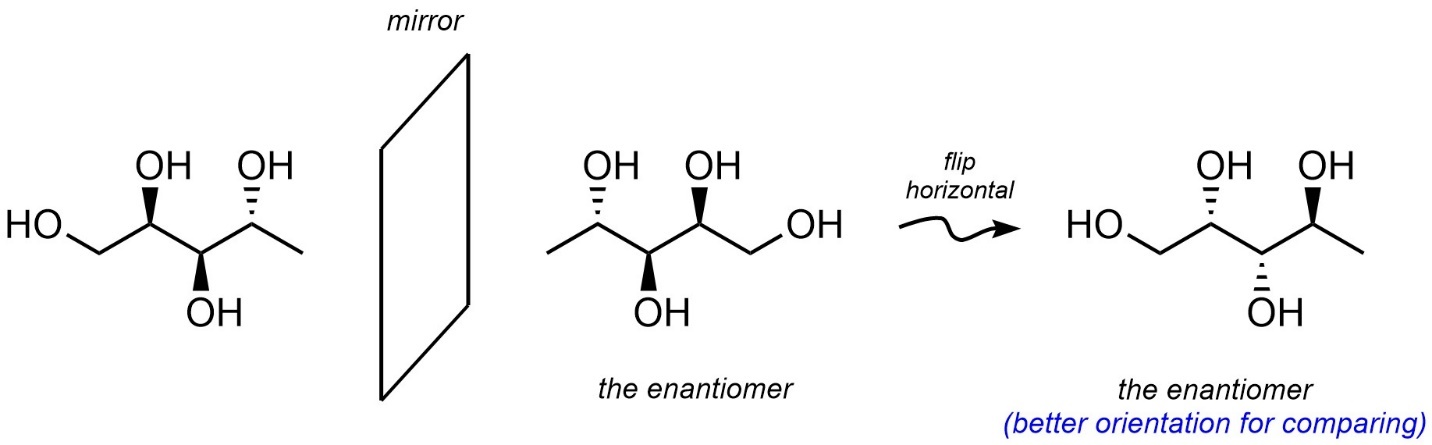
Figure 4.20 – Drawing an Enantiomer Using an Imaginary Mirror.
This highlights the other approach to drawing a compound’s enantiomer: directly invert every stereocentre (Figure 4.21). Typically, this is done by simply turning all hashed bonds into wedged bonds, and all wedged bonds into hashed bonds. This approach is often faster but can lead to errors if not all stereocentres are correctly identified. Note that only stereocentres are inverted; do not invert the geometries around alkenes (see Section 4.4). Additionally, this method will not work for molecules which are chiral but possess no stereocentres.

Figure 4.21 – Drawing an Enantiomer by Inverting all Stereocentres.
4.2.3. Stereoisomers – Diastereomers
Recall that molecules that have the same chemical formula AND their atoms are connected in the same sequence BUT they differ in the three-dimensional arrangement of those atoms are called stereoisomers. Stereoisomers can be subdivided into two main categories. All stereoisomers that are not enantiomers are classified as diastereomers (sometimes diastereoisomers).
The relationship between the top two molecules below is ‘enantiomers’ (Figure 4.22). However, the relationship between either of the top molecules and the bottom one is not. They have the same molecular formula, their atoms are connected in the same sequence, they differ in the three-dimensional arrangement of those atoms, BUT they are not enantiomers. As a result, they are diastereomers.
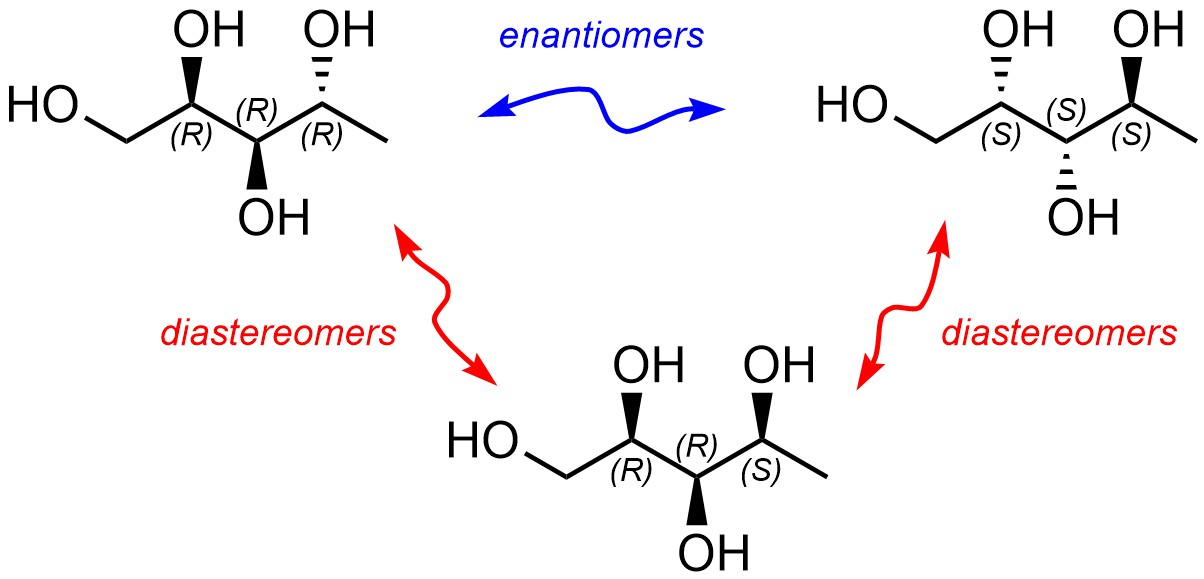
Figure 4.22 – Example of Enantiomers vs. Diastereomers.
The number of possible stereoisomers increases exponentially as each stereocentre (or stereogenic element) is added. As a result of the broad definition of diastereomer, a molecule may have one enantiomer but many diastereomers. For example, this particular compound has eight stereoisomers (Figure 4.23). Each has one enantiomer (the isomer directly above or below it). Each is then related to the other six as diastereomers.
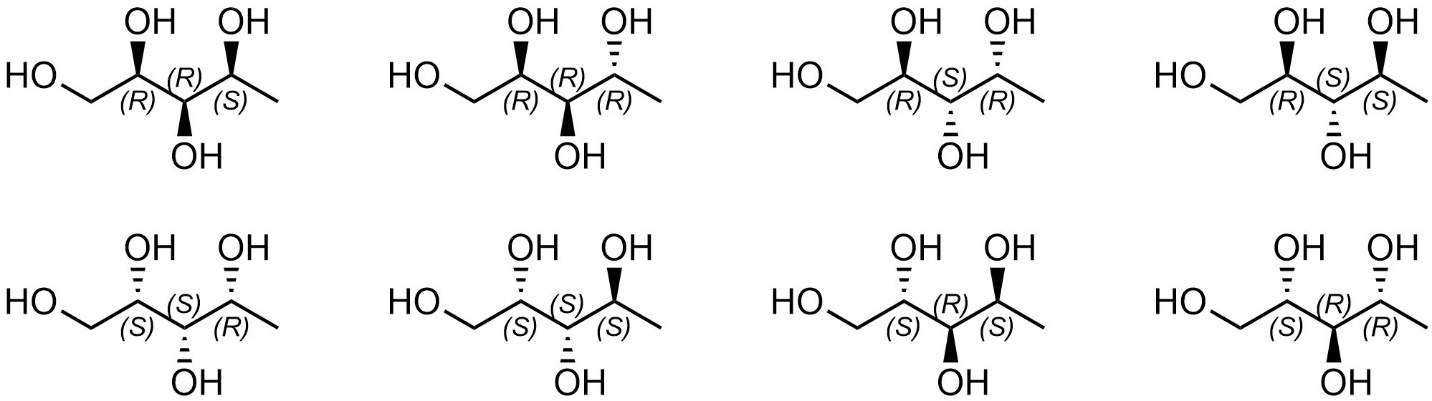
Figure 4.23 – Stereoisomers of Pentane-1,2,3,4-tetraol.
4.2.4. How to Determine the Relationship Between Two Compounds
A common task in organic chemistry is to identify and classify the relationship between two molecules. By far the simplest approach is to systematically rule out options. Remember that rotations of the whole molecule or around σ bonds are allowed (you can change the conformation and orientation).
Are the two compounds completely different? Check if the two have different molecular formulae.
Are the two constitutional isomers? Check if they have the same formula but different connectivity. Remember that constitutional isomers will have different names in the IUPAC system.
Are the two identical? Remember that conformational changes might obscure that the two are exactly the same. You may change the conformation or orientation as needed to compare.
Are the two enantiomers? Check if they are non-superposable mirror images. Sometimes it is (much) easier to quickly assign all absolute configurations to compare the two compounds.
If the answer to all previous questions was “No”, then they are diastereomers.
The following flow chart may be used as an alternative.