1.4. VSEPR Theory

Valence Shell Electron Pair Repulsion (VSEPR) theory states that the most stable three-dimensional structure for a molecule is the one in which valence electron pairs are as far apart as possible. This is intuitive; electrons are small negative charges, and negative charges repel rather than attract each other. In practical terms VSEPR theory amounts to keeping groups (attached atoms or lone pairs) as far apart from each other as possible.

1.4.1. Linear vs. Trigonal Planar vs. Tetrahedral Geometries

If there are two groups then maximizing the distance between them makes a Linear geometry (Figure 1.18). The two groups are on opposite sides of the central point (atom) to keep as far from each other as possible. The typical angle between them is thus 180°.

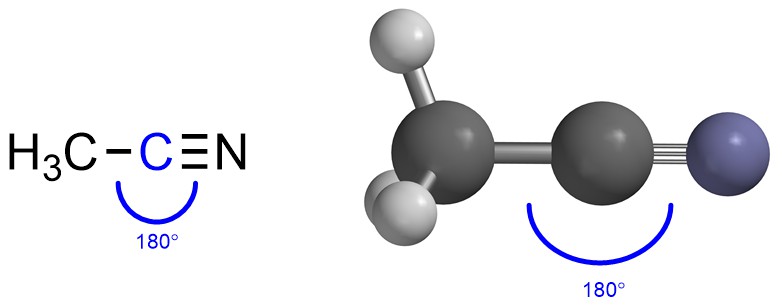
Figure 1.18 – Example of Linear Geometry with the Angle Highlighted.

If there are three groups then maximizing the distance between them makes a Trigonal Planar geometry (Figure 1.19). The three groups are arranged in a triangle around the central point (atom) to keep as far from each other as possible. The typical angle between them is thus around 120° (this varies slightly depending on what the groups are, but the variation is not normally important).

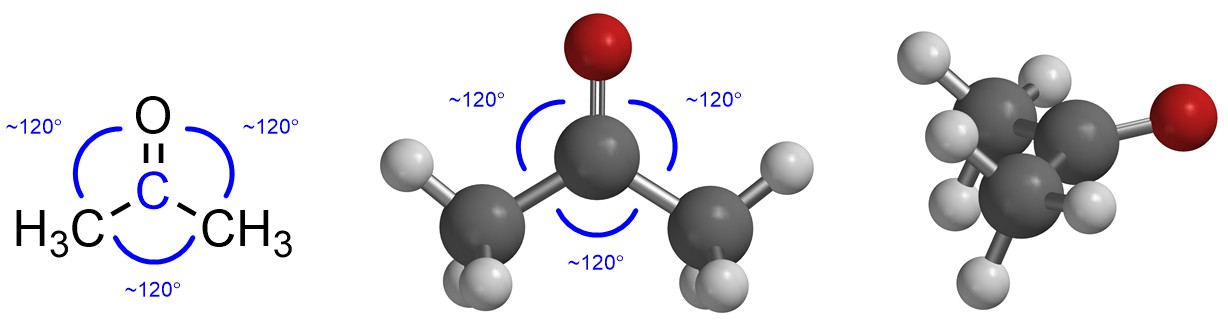
Figure 1.19 – Example of Trigonal Planar Geometry with the Angles Highlighted.

If there are four groups then maximizing the distance between them makes a Tetrahedral geometry (Figure 1.20). This is the first truly three-dimensional geometry. If the four groups were instead arranged two-dimensionally (i.e. as a square around the central point) then the angle between them would be approximately 90°. By instead arranging the four groups three-dimensionally as a tetrahedron the angle, and by extension the distance, between them increases to around 109°. This again varies slightly depending on the exact groups, but the idea of maximal distance is upheld. For those unfamiliar with the shape, a tetrahedron is equivalent to a four-sided pyramid where each of the three sides and the bottom are equilateral triangles.

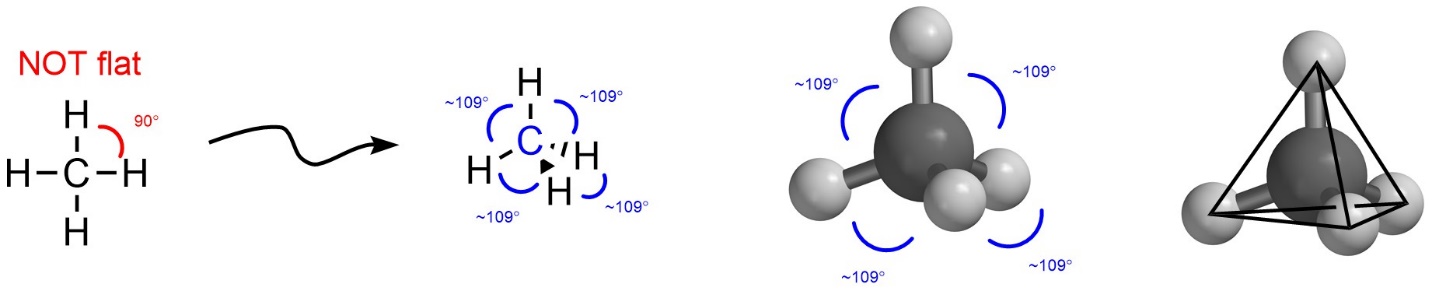
Figure 1.20 – Example of Tetrahedral Geometry with the Angles Highlighted.

Additional complex geometries are possible and may be encountered in other subjects, such as inorganic chemistry, but are not relevant in simple organic systems.

1.4.2. Older Conventions

Some older textbooks denote a difference between lone pairs and atoms when talking about ‘groups’ to describe geometry (Figure 1.21). These are usually referred to as electron and molecular geometries.

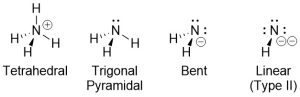
Figure 1.21 – Examples of Electron and Molecular Geometries.

So-called molecular geometries have no practical (or theoretical) uses and may be ignored. In the examples above the correct description for the geometry of all four nitrogen atoms would simply be tetrahedral.