3.4. Types of Strain in Molecules
In any given system most things like to rest in the lowest possible energy state. This is not always possible. For example, there may be geometric or physical constraints on what angles are required, or how close two substituents have to be to each other. When molecules are forced to adopt some condition that is not ‘ideal’, they experience strain. Experiencing strain raises the amount of energy needed to exist. There are several common types of strain that molecules may experience.
3.4.1. Angle Strain
Angle Strain arises from bond angles deviating from their ideal values. It costs energy to do this because the orbitals can not overlap as well, which leads to weaker bonds. There are several reasons why angle strain may occur, but the most common is a geometric constraint (Figure 3.5). For example, in cyclopropane the three carbons form a triangle. The internal angles of an equilateral triangle are 60°. The carbons are all sp3 hybridized. Ideally, they would have angles of 109° between their substituents. Since this is not possible, they experience angle strain. The energy of the system (the energy required to exist) increases and the bonds become weaker compared to ‘normal’ C-C σ bonds.
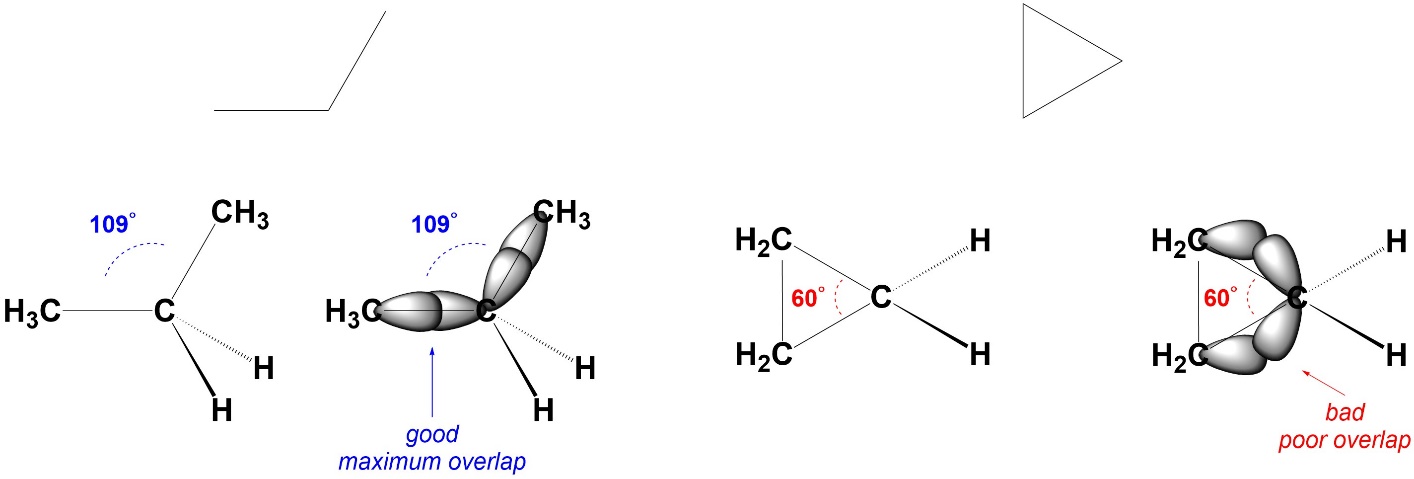
Figure 3.5 – Example of Angle Strain.
3.4.2. Torsional Strain
An accurate definition of torsional strain requires knowledge beyond the scope of an introductory course. Instead, a (highly) simplified explanation is more useful. Recall that electrons have small negative charges associated with them. A negative charge repulses other negative charges. Torsional strain occurs when the electron clouds from two atoms that are separated by exactly three bonds come close together (Figure 3.6). Torsional strain is very common and usually has only a small energy cost associated with it.
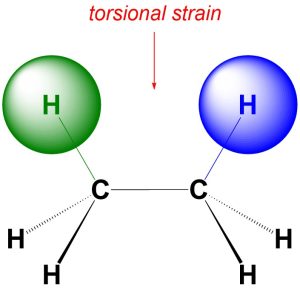
Figure 3.6 – Example of Torsional Strain.
The exact reason why the two groups must be separated by three bonds is the complex part of the definition; it is not only because they are very close together. As a result, if they are separated by more or fewer than three bonds torsional strain does not occur (Figure 3.7). Note that this does not mean there will be NO strain between these groups (see Section 3.4.3.).
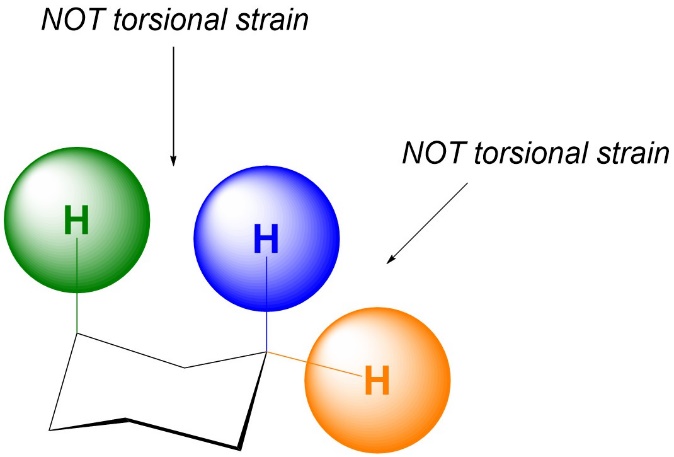
Figure 3.7 –Examples of Lack of Torsional Strain due to Incorrect Number of Bonds Separating Atoms.
3.4.3. Steric Strain
In steric strain the two electron clouds overlap (interpenetrate) slightly (Figure 3.8). Steric strain also does NOT require a specific number of bonds separating the groups. Steric strain is associated with significantly larger energy costs than torsional strain and plays a key role in many chemical reactions. As the electron clouds on the two groups increase in size more overlap occurs, and the energy cost associated with the interaction increases. In other words, bigger groups cause larger steric interactions.
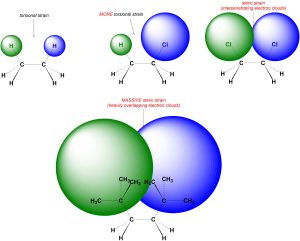
Figure 3.8 – Torsional Strain vs. Steric Strain.
Because the electron clouds need to interpenetrate they typically need to be much larger than the electron clouds on hydrogens. As a result, steric interactions between hydrogens and other groups are somewhat uncommon outside of specific situations (see Section 3.6.4.5). It is possible for there to be steric interactions between the electron clouds of two hydrogens, but this normally has very specific geometric requirements. Unless otherwise noted, assume all interactions between two hydrogens experience torsional, not steric, strain.
If there are two large groups attached to the same atom their electron clouds can interpenetrate. This usually requires very large groups with large electron clouds (Figure 3.9). Whether these constitute steric interactions is debatable and usually varies depending on the groups. In this text assume there is no steric strain between two groups attached to the same atom unless otherwise noted.
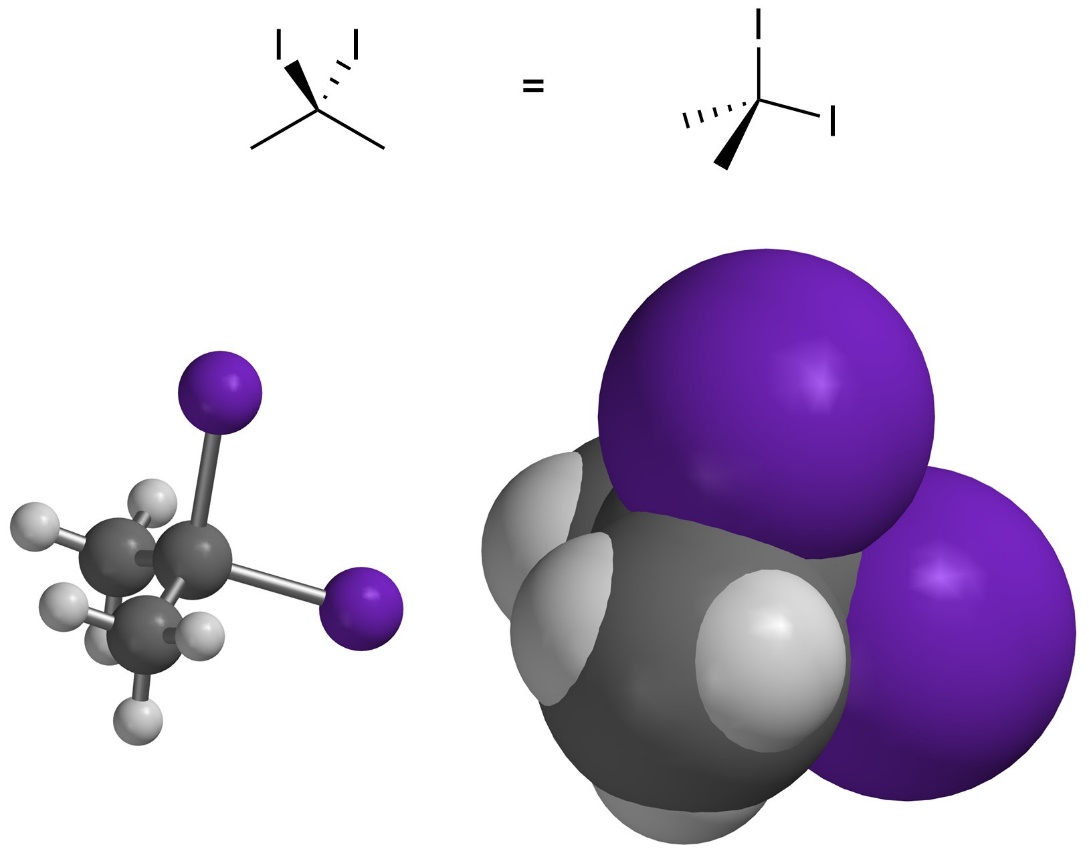
Figure 3.9 – Interpenetration of Electron Clouds from Groups Attached to the Same Atom.

