5.4. Reaction Coordinates
When encountering reaction coordinates (energy diagrams) be aware that this is an introductory organic chemistry text, not a physical chemistry text. However, it is important to understand the basic terminology and applications of energy diagrams as they can add clarity or be useful for explaining reactivity.
5.4.1. Terminology
A generic reaction coordinate is useful for seeing important aspects of these diagrams (Figure 5.16). The starting materials are the compounds before the reaction. Intermediates are compounds made during the reaction that continue undergoing transformations to eventually form the products. The products are the new compounds made at the end of the reaction.
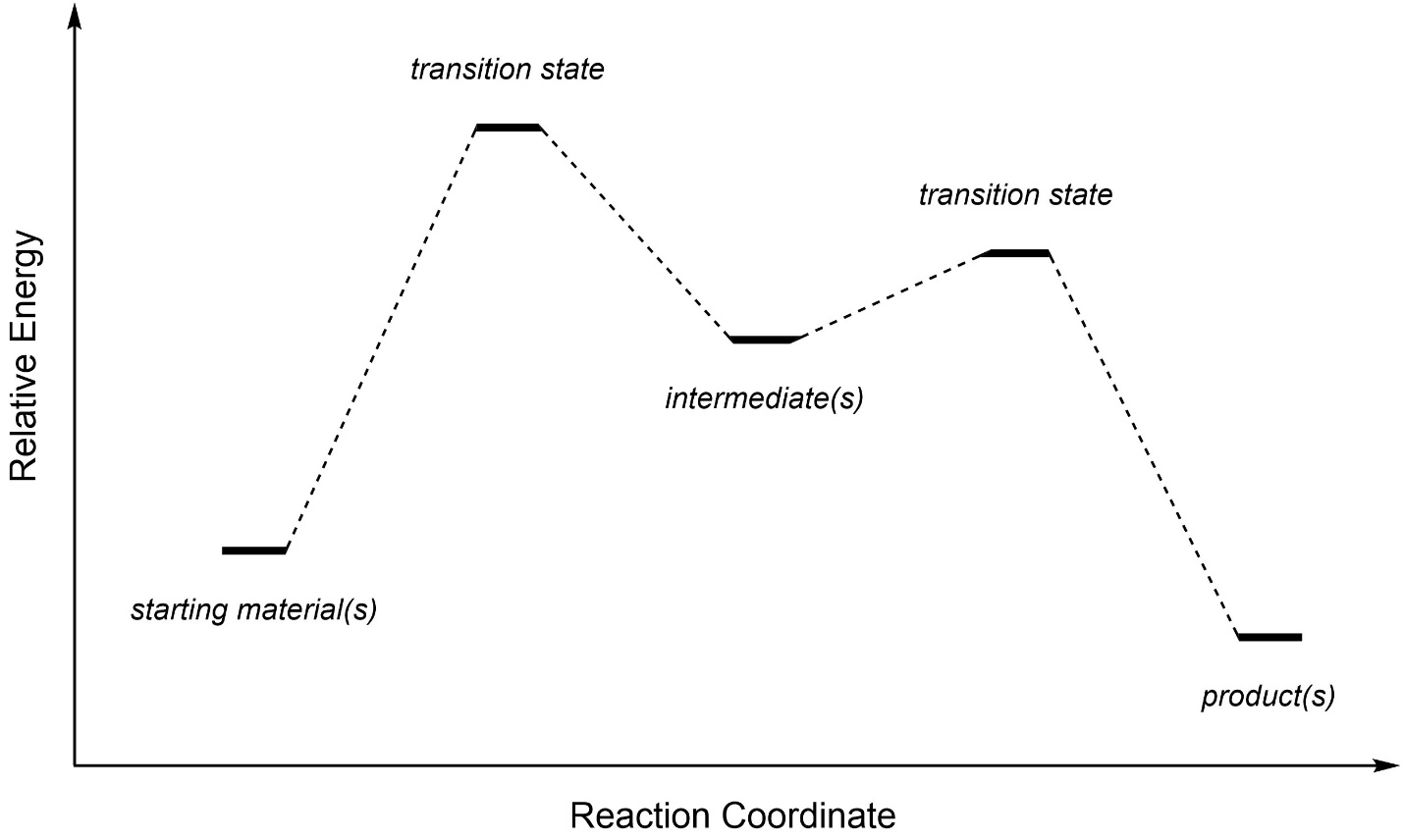
Figure 5.16 – Example of a Reaction Coordinate Highlighting Starting Materials, Intermediates, Transition States, and Products.
As the starting material becomes an intermediate, and as an intermediate becomes a product, they pass through transition states. Transition states are NOT a different kind of compound, they are what the compound(s) look like while undergoing a transformation. It may help to imagine a transition state as being analogous to the exact moment that a baseball is struck by a bat. Although we often draw the energy surface as discrete lines, remember that the reality is (probably) a curved surface (Figure 5.17).
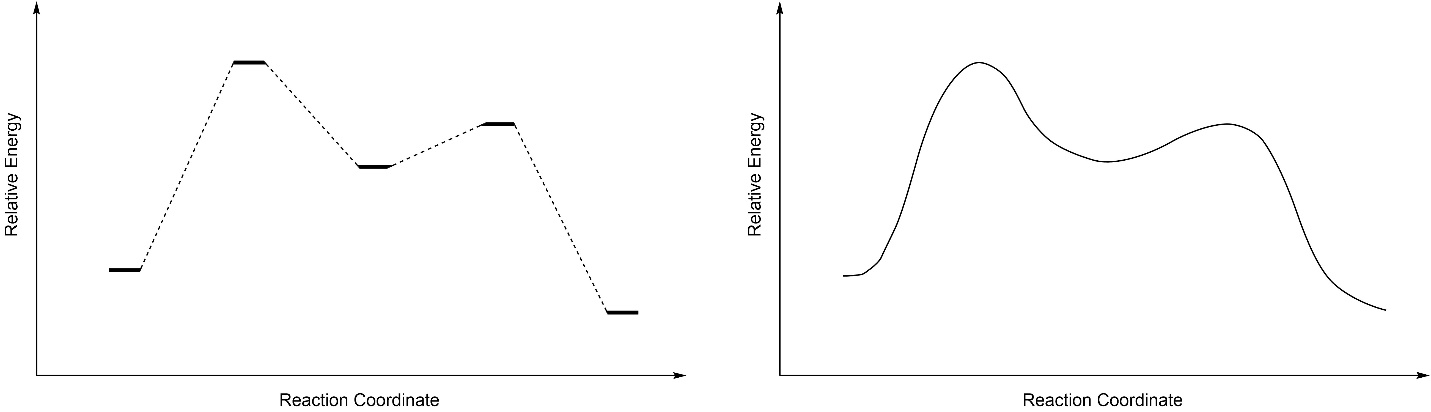
Figure 5.17 – Simplified and Curved Reaction Coordinates.
The energy difference between a starting material/intermediate and the transition state beside it is an activation energy (usually symbolized as Ea or ΔG‡; Figure 5.18). This is the amount of energy needed for the compounds to pass through the transition state and become the next species in the pathway. If there is only one ΔG‡ then it is the rate-determining step (sometimes called rate-limiting step). If there are more than one ΔG‡ then whichever is largest is the rate-determining step. Note that this means the rate-determining step is not necessarily the transition state with the highest energy. The difference between the transition state and what precedes it is what is important.
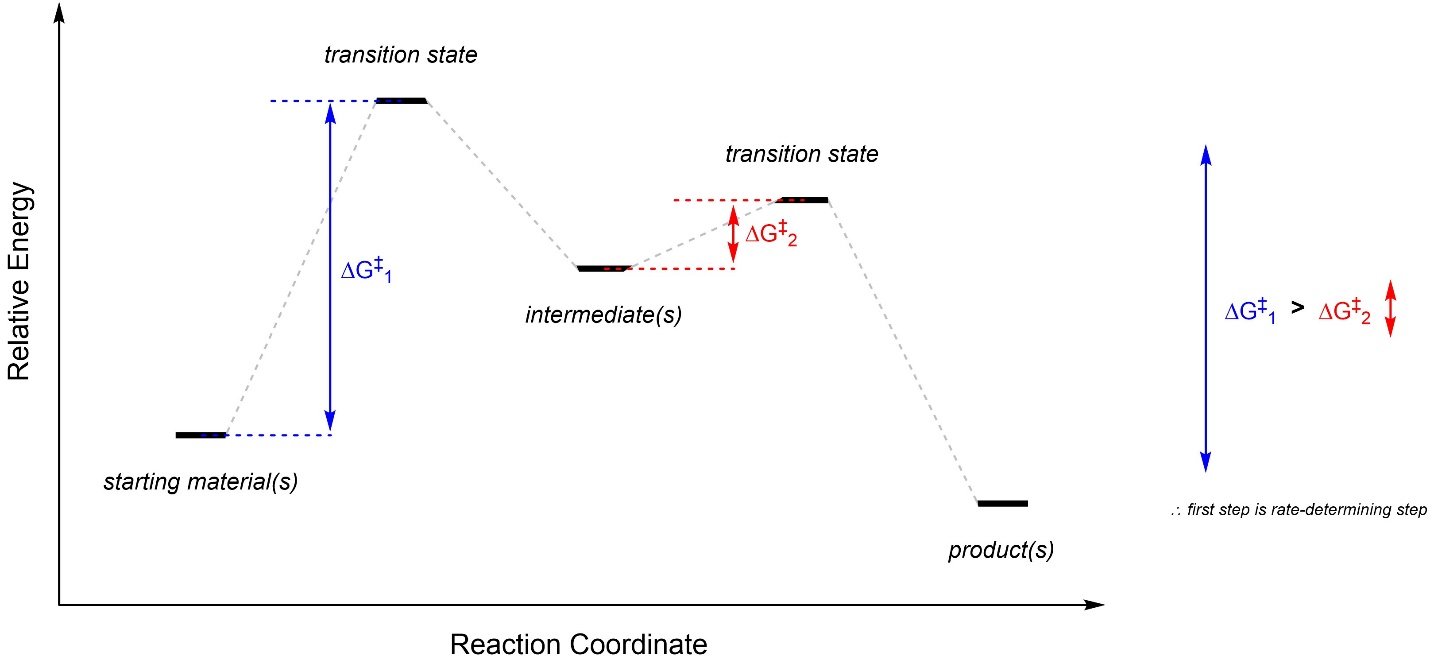
Figure 5.18 – Example of a Reaction Coordinate Highlighting Activation Energy.
In recent years the concept of a “rate-determining step” has come into question, primarily because it only works well for a small selection of very simple reactions. Technically the actual rate of the reaction is determined by the largest difference between an energy minimum and a later energy maximum. This is called the energetic span. For simple reactions this is often equivalent to the largest ΔG‡, but not necessarily; for many reactions the overall rate is not controlled by a single “step”. This parameter is (much) more accurate when defining reaction rates, but its use is not currently as widespread.
If the final products are lower in energy than the starting materials, then the reaction is exergonic (“energy releasing”; Figure 5.19). If the final products are higher in energy than the starting materials, then the reaction is endergonic (“energy absorbing”). The terms ‘exothermic’ and ‘endothermic’ may be more familiar, but these refer only to enthalpy (ΔH) not free energy (ΔG). It may be useful to recall that “ΔG = ΔH – TΔS”, so free energy is more accurate to use and also accounts for enthalpy. The energy difference between the starting materials and the products is the change in free energy at standard conditions (ΔG°RXN or ΔG°).
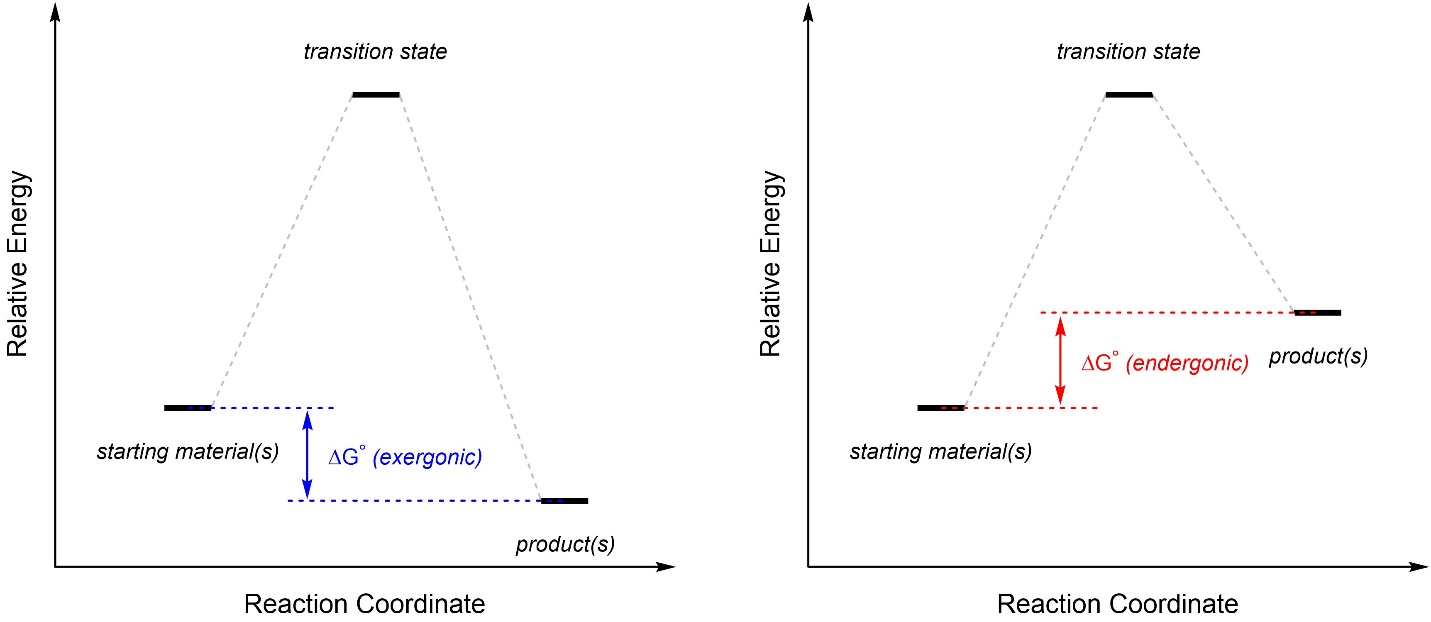
Figure 5.19 – Examples of Exergonic and Endergonic Reaction Coordinates Highlighting the Change in Free Energy.
Although slightly beyond the scope of this text, a brief discussion of kinetics and thermodynamics may be useful to some readers.
Kinetics relates to the overall rate of the reaction. With respect to reaction coordinates, kinetics is only concerned with ΔG‡ values and the rate-determining step; the energies of the starting materials, intermediates, and products are irrelevant. Technically, the exact energies of the transition states are also irrelevant. Only the difference (ΔG‡) between the energies matters. The number of steps in the reaction also does not matter. For example, a reaction with one step (one transition state) can be slower than a reaction with fifty steps.
Thermodynamics relates to the energy absorbed or released in the reaction. With respect to reaction coordinates, thermodynamics is only concerned with ΔG° values; the energies of the intermediates and transition states are irrelevant. Technically, the exact energies of the starting materials and products are also irrelevant. Only the difference (ΔG°) between the energies matters.
5.4.2. Practical Uses of Reaction Coordinates
Most practical applications of reaction coordinates lie beyond the scope of an introductory text. Equilibrium ratios, the Arrhenius equation, Hammond’s Postulate, the Curtin-Hammett Principle, chemo-/regio-/stereo-selectivity arguments, and more can use the values of (or relative positions of) species in reaction coordinates to determine, express, or explain many things about chemical reactions.
At an introductory level, examining the reaction coordinate can reveal how many steps are involved in a reaction. This can have important implications for describing the mechanism (see Chapters 11 and 12).
Deciding which step is rate-determining is possible by comparing activation energies. Then, understanding which compounds are involved in the rate-determining step (and how the transition state looks) can help with understanding why some reactions can be accelerated by certain effects while others cannot. The relative activation energies of reactions can be compared to determine which of the reactions will be faster.
When discussing “fast” reactions like acid-base chemistry (see Chapter 6) knowing if the reaction is exergonic or endergonic can help compare relative acidities. Comparing ΔG° values may accomplish the same task.
Although a deep understanding and application of reaction coordinates requires a great deal more discussion and detail than appropriate at an introductory level, developing some understanding at this stage can be very helpful both now and in further studies.

