3.6. Strain and Conformation in Cyclic Molecules

When molecules contain cyclic structures (rings) they may experience additional strain as a result of the conformations available to them. Being in a ring limits flexibility by tethering the two ‘ends’ together, so they are not able to rotate independently of each other.

As the ring size increases the number of conformations available to it increases. Initially the amount of strain decreases as the rings get larger (as angle and torsional/steric strain decreases). When the ring contains 6 atoms the strains are minimized and a high degree of stability is achieved. Then, as ring size continues to increase strain is reintroduced to the system; instead of being ‘too small’ the bond angles are forced to be ‘too large’ and angle strain is experienced again. Eventually this minimizes again for sufficiently large rings. Since the number of conformations available increases (exponentially) as ring size increases, at an introductory level analysis of rings up to six atoms is sufficient.

3.6.1. 3-Membered Rings

Recall that angle strain arises from bond angles deviating from their ideal values. It costs energy to do this because the orbitals can not overlap as well, which leads to weaker bonds. There are several reasons why angle strain may occur, but the most common is a geometric constraint (Figure 3.20). For example, in cyclopropane the three carbons form a triangle. The internal angles of an equilateral triangle are 60°. The carbons are all sp³ hybridized. Ideally, they would have angles of 109°. Since this is not possible, they experience a significant amount of angle strain.

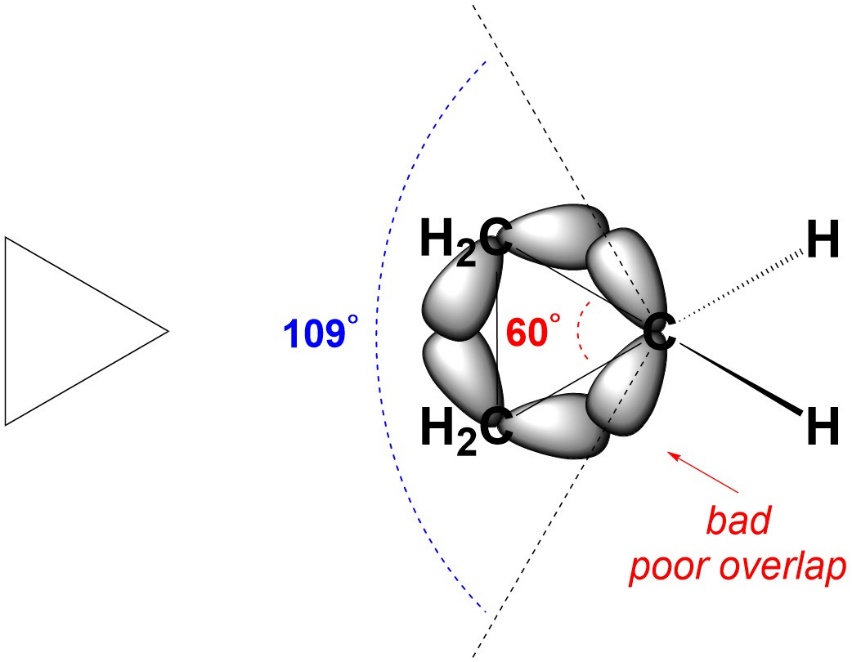
Figure 3.20 – Angle Strain in Cyclopropane.

When drawn in two dimensions rings appear to be planar (flat). However, this is rarely true. As cyclopropane contains only three atoms in the ring, it must be planar (three points must all lie in one plane, it is not possible to arrange them otherwise). As a result it experiences significantly more torsional strain than other sizes of rings.

Recall that torsional strain occurs when the electron clouds from two atoms separated by exactly three bonds other come close together (Figure 3.21). Since cyclopropane is planar, looking down any of its C-C σ bonds reveals that all hydrogens are eclipsing one another, leading to a high degree of torsional strain.

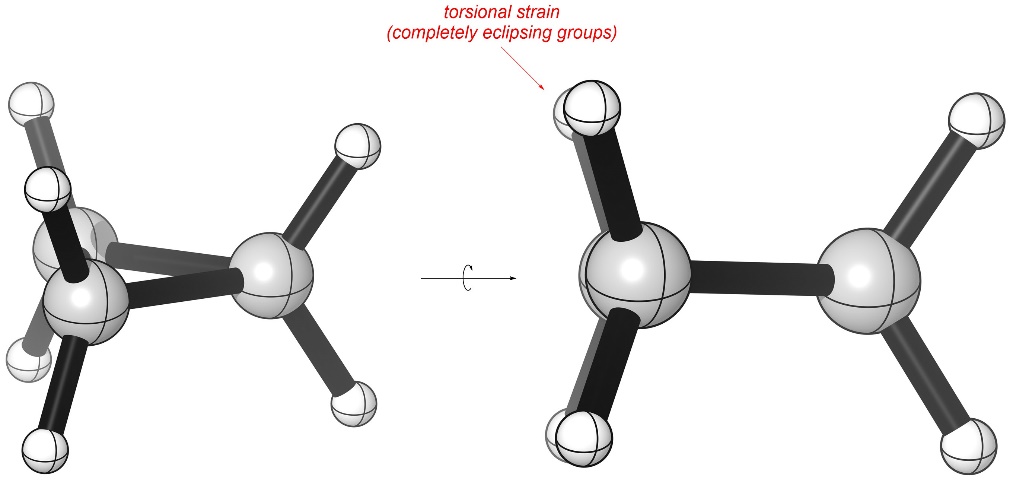
Figure 3.21 – Torsional Strain in Cyclopropane.

These issues apply to other types of 3-membered ring systems. As a result, generally rings this size are uncommon in nature (because they often degrade relatively quickly) and may be challenging to make synthetically (because they require a significant amount of energy to be formed).

3.6.2. 4-Membered Rings

Unlike 3-membered rings, 4-membered rings can adopt non-planar conformations. These are commonly called “butterfly conformers”. Being able to adopt non-planar conformations allows molecules like cyclobutane to reduce some of the strain from being cyclic.

Increasing the ring size from 3 to 4 atoms reduces the angle strain. In a planar conformation cyclobutane would have internal angles of 90°, which still differs from 109° but is significantly closer to it (Figure 3.22). However, adopting a planar conformation would keep the torsional strain experienced in cyclobutane, so instead the ring bends to butterfly conformers.

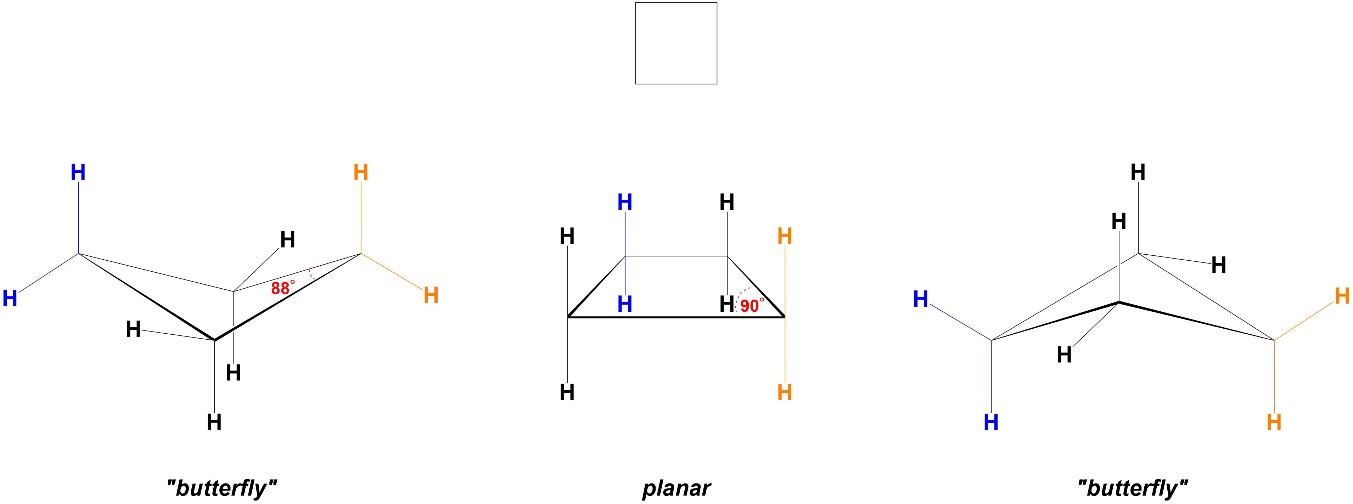
Figure 3.22 – Angle Strain and Conformations in Cyclobutane.

These have internal angles of 88° but the energy lost from having a slightly smaller angle is more than offset by reducing torsional strain (Figure 3.23). Although the groups continue to eclipse each other slightly, as they move towards a staggered orientation the amount of torsional strain they experience is reduced.

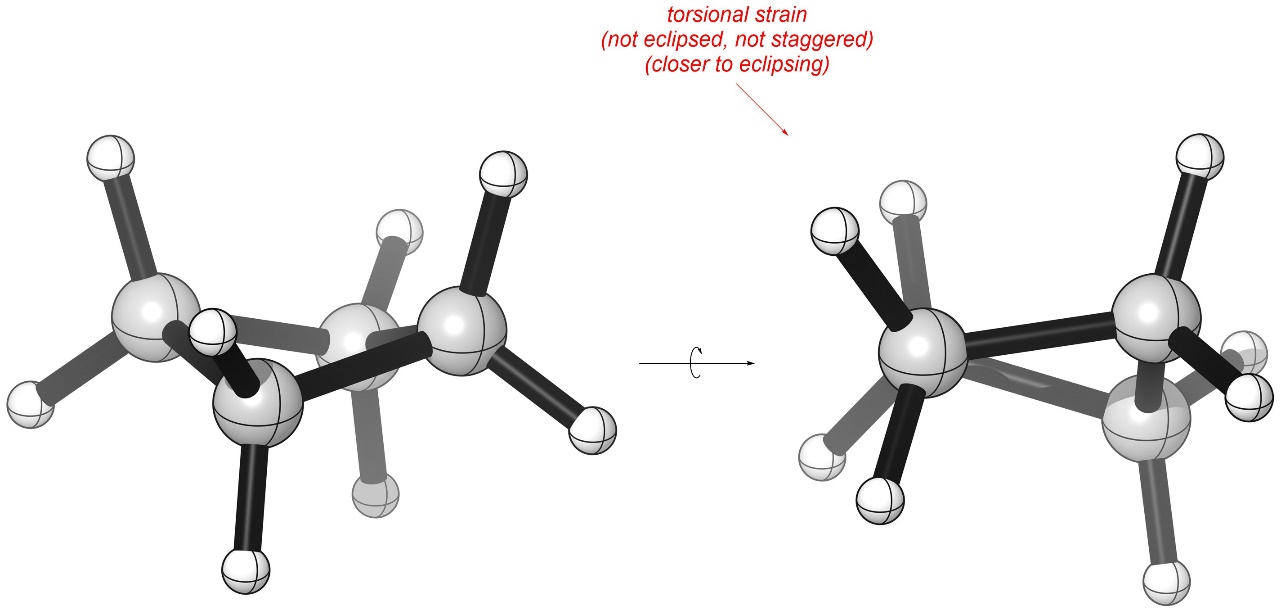
Figure 3.23 – Torsional Strain in Cyclobutane.

The two butterfly conformers may interconvert by passing through the planar geometry (Figure 3.24). Changing between the lowest energy conformations of a ring is called ring inversion (sometimes ring flip). For cyclobutane the barrier is very low, and the two conformations rapidly interconvert. Note that the older term ‘ring flip’ is very misleading; the ring is not flipping, the bonds are rotating to change the conformation.

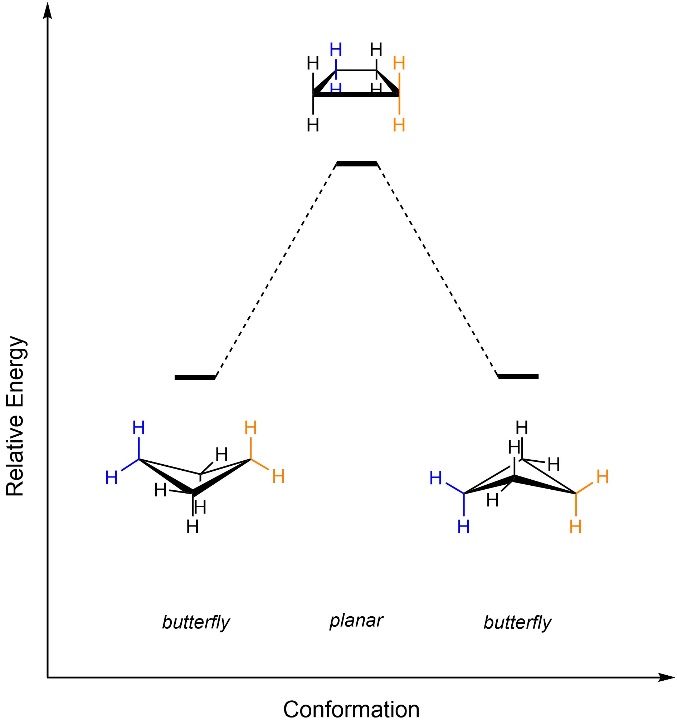
Figure 3.24 – Energy Diagram for Ring Inversion of Cyclobutane.

These same factors apply to other types of 4-membered ring systems. As a result, generally rings this size are uncommon in nature (because they often degrade relatively quickly) and may be challenging to make synthetically (because they require a significant amount of energy to be formed).

3.6.3. 5-Membered Rings

Like 4-membered rings, 5-membered rings can adopt non-planar conformations. These are commonly called “envelope conformers”. Being able to adopt non-planar conformations allows molecules like cyclopentane to reduce most of the strain from being cyclic.

Increasing the ring size from 4 to 5 atoms further reduces the angle strain. In a planar conformation cyclopentane would have internal angles of 108°, which is very close to 109° (Figure 3.25). However, adopting a planar conformation would keep the torsional strain experienced in cyclopropane, so instead the ring bends to envelope conformers. There are 10 envelope conformers in total (one for each of the five atoms being “above” the plane of the other four, and one for each being “below”). Drawing all 10 conformers is more tedious than challenging and would not be expected at an introductory level.

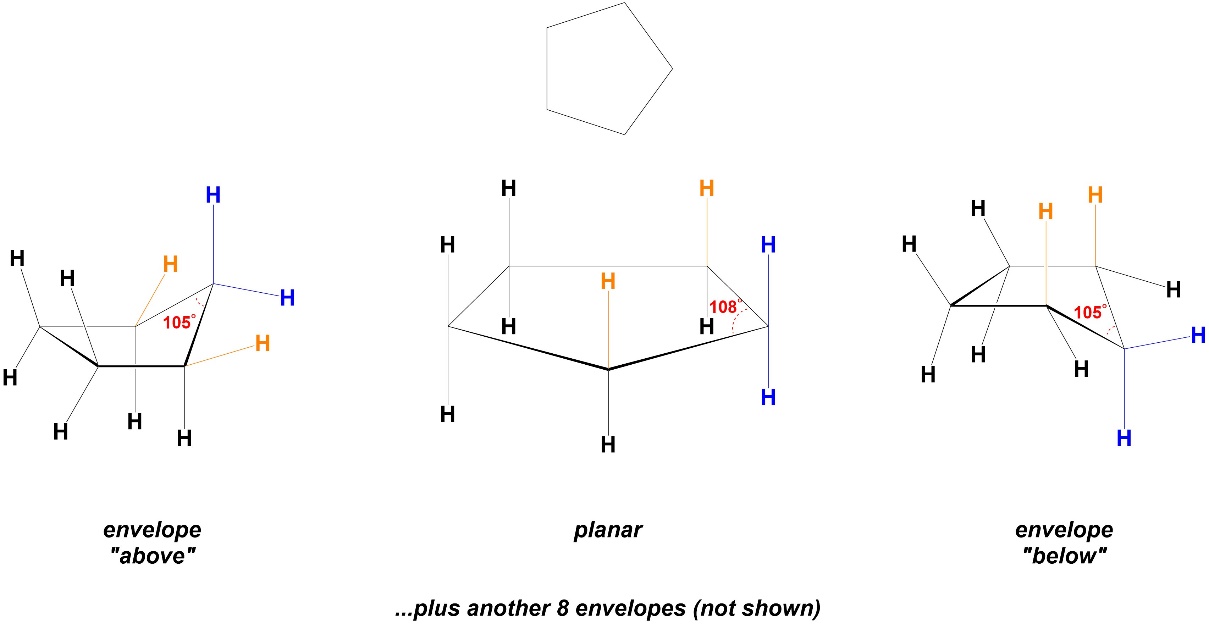
Figure 3.25 – Angle Strain and Conformations in Cyclopentane.

These have internal angles of 105°, but the energy lost from having a slightly smaller angle is more than offset by reducing torsional strain (Figure 3.26). Although the groups are not fully staggered the amount of torsional strain they experience is very low.

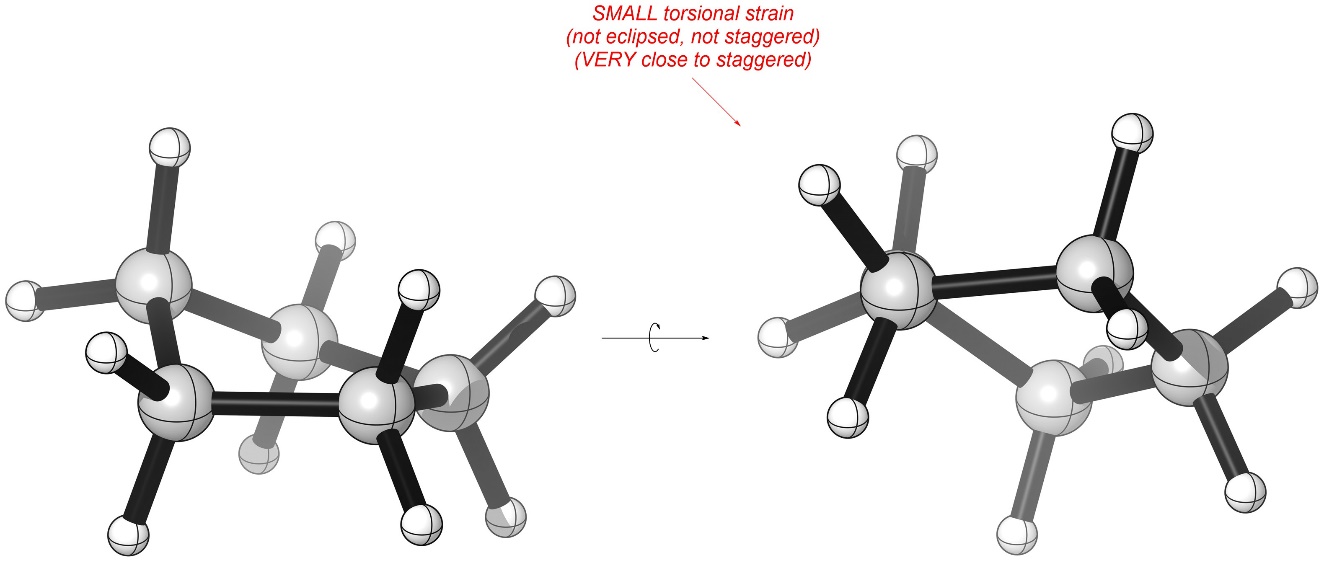
Figure 3.26 – Torsional Strain in Cyclopentane.

The ten envelope conformers interconvert rapidly at room temperature. This is difficult to show graphically given the number of possible conformation conversions. Instead, it is sufficient to say that each atom in the ring “takes turns” being out of plane with the others.

These same factors apply to other types of 5-membered ring systems. As a result, generally rings this size are common in nature (because they are generally stable) and are often easy to make synthetically (because there is little strain, amongst other reasons).

3.6.4. 6-Membered Rings

6-Membered rings are significantly more complex than the previous cases.

Like 5-membered rings, 6-membered rings can adopt non-planar conformations. The two most stable of these are commonly called “chair conformers”. Being able to adopt non-planar conformations allows molecules like cyclohexane to eliminate the strain from being cyclic.

Increasing the ring size from 5 to 6 atoms has conflicting effects on angle strain. In a planar conformation cyclohexane would have internal angles of 120°, which is moderately larger than 109° (Figure 3.27). This would add angle strain to the torsional strain experienced in cyclopropane, so instead the ring bends to chair conformers. There are two chair conformers.

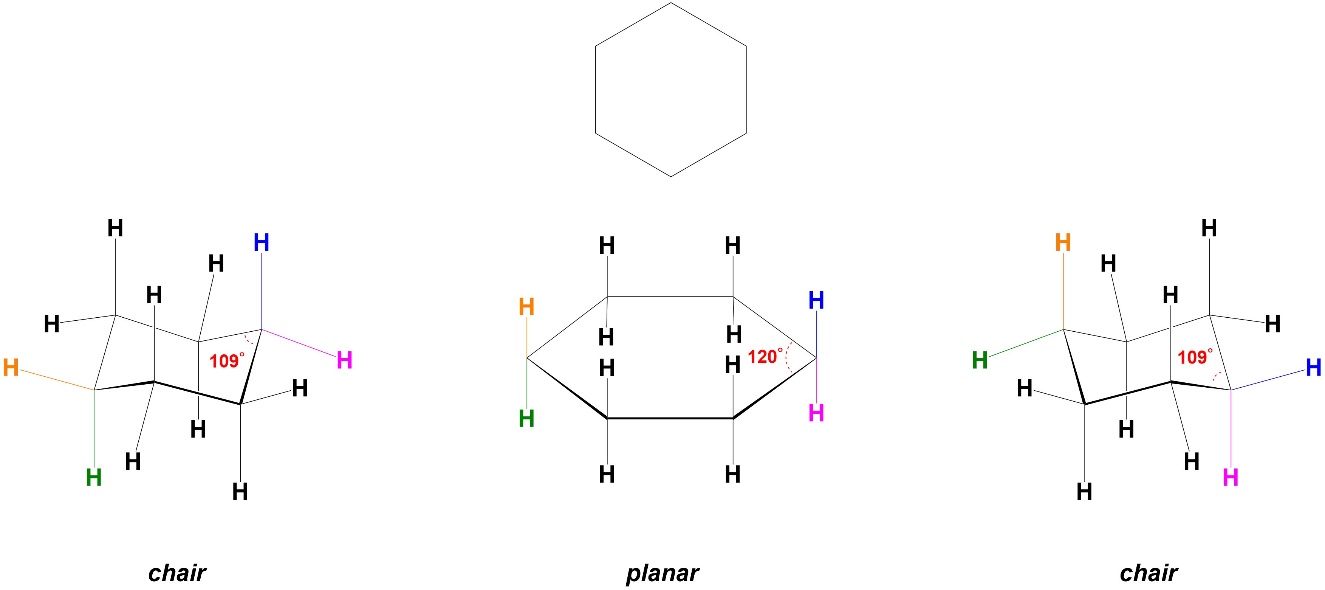
Figure 3.27 – Angle Strain and Conformations in Cyclohexane.

While in a chair conformation all bond angles are 109° (there is no angle strain). Additionally, looking along any C-C bond shows that all groups adopt a staggered conformation (there is no torsional strain; Figure 3.28). This means that among ring systems 6-membered rings are by far the most stable.

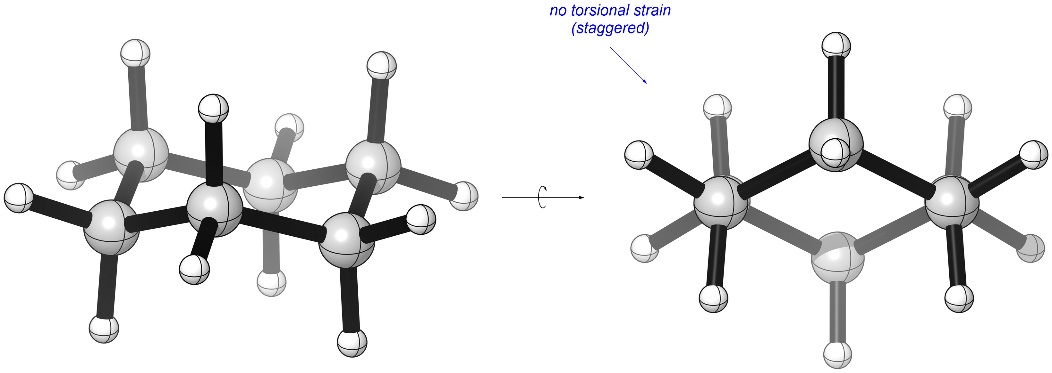
Figure 3.28 – Lack of Torsional Strain in Cyclohexane.

The two chair conformers usually interconvert readily at room temperature. This depends significantly on what, if any, substituents there are (see Section 3.6.4.5). While undergoing inversion the ring passes through three other important conformations (Figure 3.29): the half-chair, twist boat, and boat (followed by the other twist boat, half-chair, and finally the other chair conformation). These other conformations play critical roles for many biologically and pharmacologically important molecules. However, they are generally regarded as challenging to draw or evaluate and are best left for more advanced texts for in-depth analysis. Importantly, at no point does the molecule adopt a planar conformation.

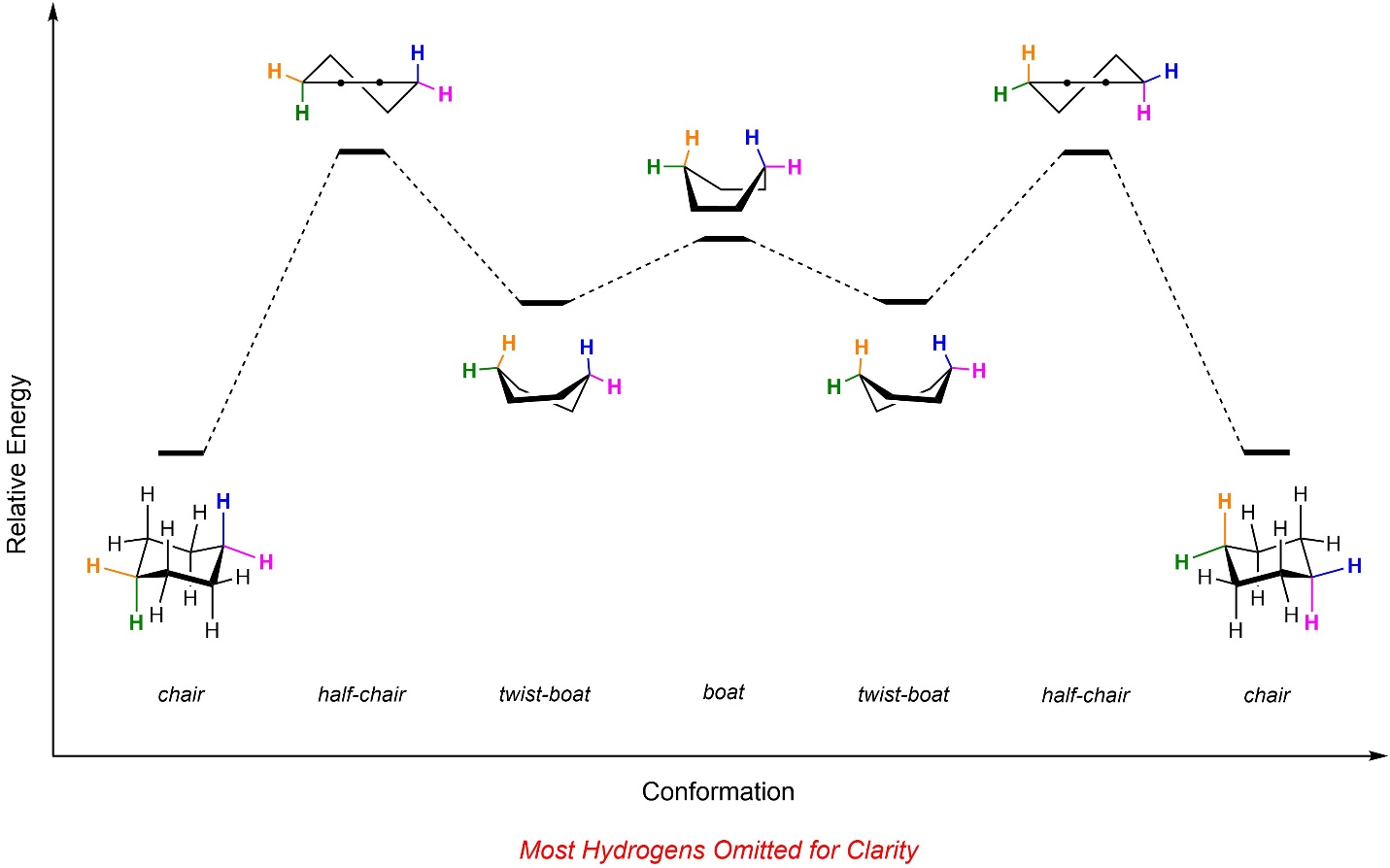
Figure 3.29 – Energy Diagram for Ring Inversion of Cyclohexane.

These same factors apply to other types of 6-membered ring systems. As a result, rings this size are very common in nature (because they are very stable) and are often easy to make synthetically (again, this depends significantly on the substituents on the ring).

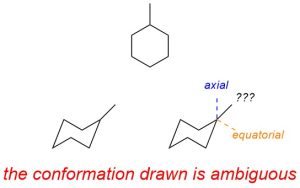
3.6.4.1. Axial and Equatorial Groups

There are special terms to describe the orientation of attached groups (substituents) in chair conformations (Figure 3.30). There are 6 groups that point directly up or down from the ring. These are called the axial groups (they are aligned with the Z-axis). There are 6 groups that point out from the ring and towards the mid plane of the ring (3 slightly up, 3 slightly down). These are called the equatorial groups (they point to the “equator” of the molecule).

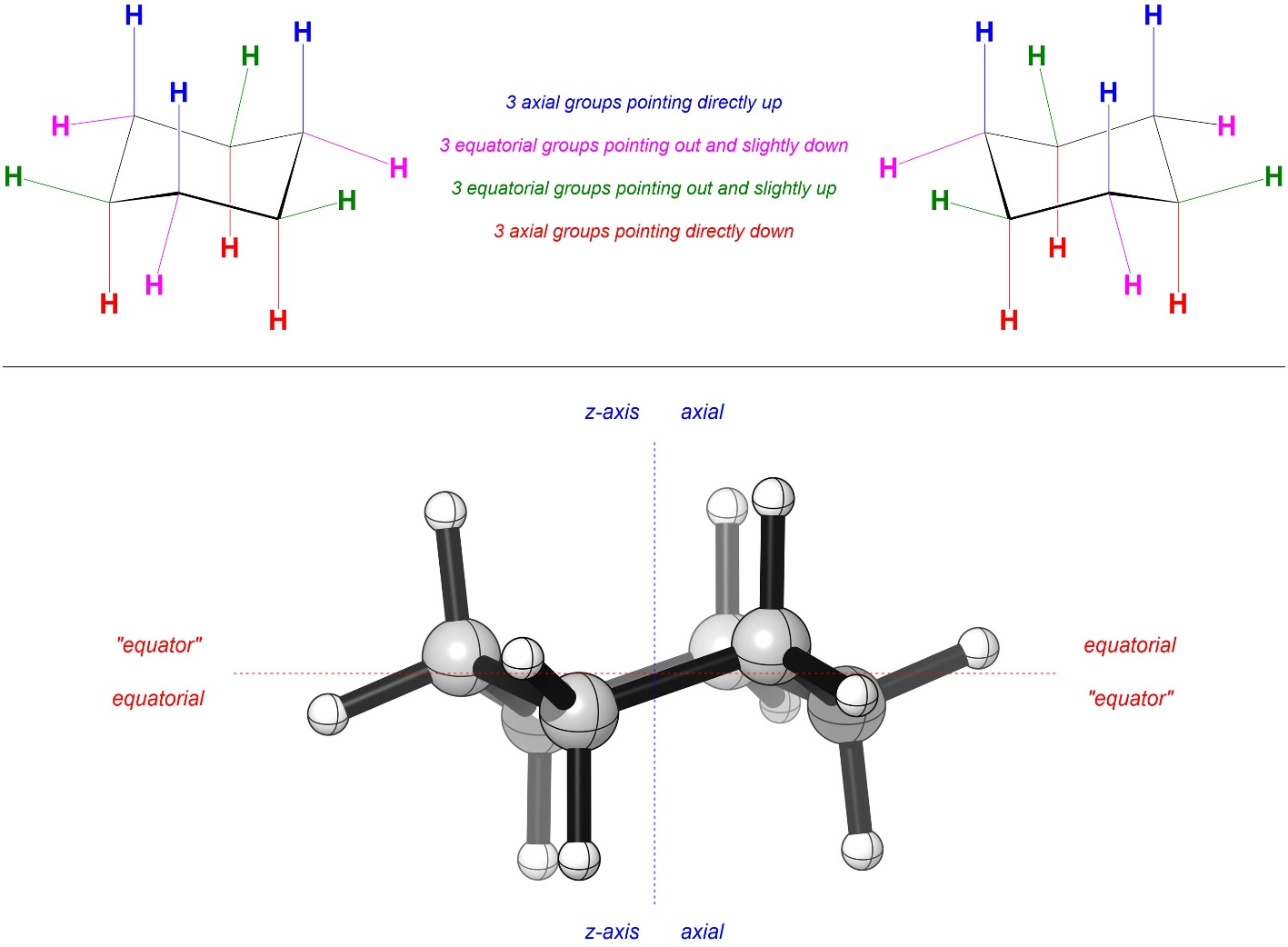
Figure 3.30 – Axial vs. Equatorial Groups in Cyclohexane.

When the conformation changes from one chair to the other (ring inversion), all axial groups become equatorial groups, and all equatorial groups become axial groups (Figure 3.31). It is very important to remember that these two chairs are conformations of the same molecule; no bonds are breaking, no groups are “moving” to new positions.

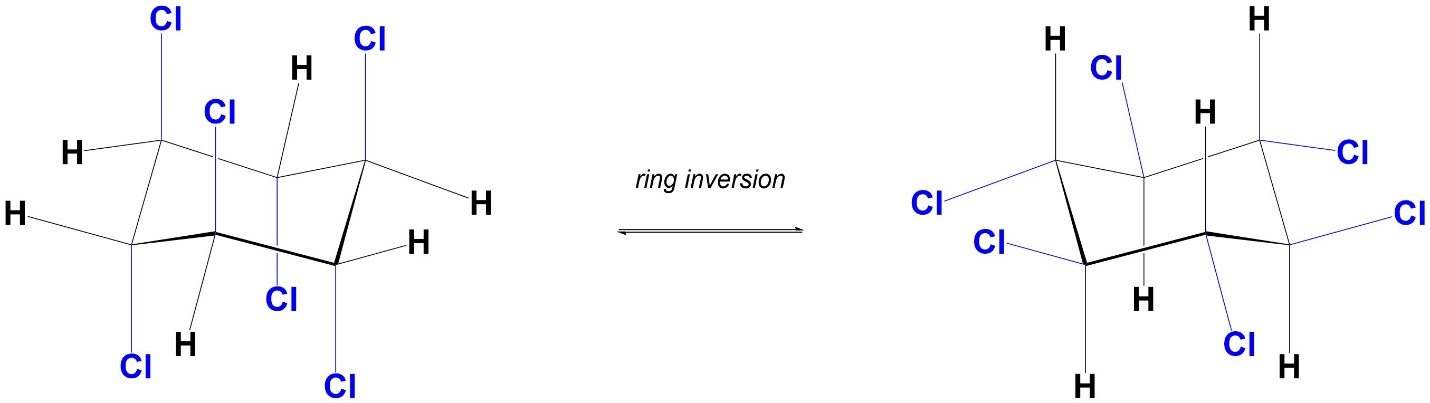
Figure 3.31 – Axial and Equatorial Groups Interchange with Ring Inversion.

3.6.4.2. Ways to Visualize Chair Conformers

There are multiple conventions for depicting chair conformations. These images are all equivalent and equally valid (Figure 3.32). Generally, texts make use of the rightmost convention, which attempts to clarify which atoms are closest to the viewer using wedged bonds and shows all groups explicitly. However, when drawing chair conformations any of these is acceptable.

Figure 3.32 – Different Conventions for Depicting Chair Conformations.

The orientation of the ring changes slightly between drawings of the two chairs. As a result, it is sometimes difficult to follow which atoms correspond to each other between representations. By visualizing the rings in a slightly different orientation it becomes clearer which positions are equivalent. Before this approach is explained it is vital to emphasize that this is only a tool for visualization. Chairs should not be drawn this way. There are several reasons why chairs are drawn in the other orientation, but the simplest is that it is unambiguous which groups are axial and which are equatorial.

If the two chair conformations are rotated slightly it becomes clear that four of the six atoms in the ring occupy a plane (numbered 2, 3, 5, and 6; Figure 3.33). Then, one of the other atoms lies above this plane and the other lies below it. When the ring inversion occurs the atom that was above the plane comes below the plane, the atom that was below the plane comes above the plane, and the four atoms in the plane remain in the plane. The whole ring does not rotate, only the atoms that were not in the plane move. This ignores the groups attached to those atoms (hydrogens in this case), which also move during the ring inversion. This is most easily seen if the carbons are numbered.

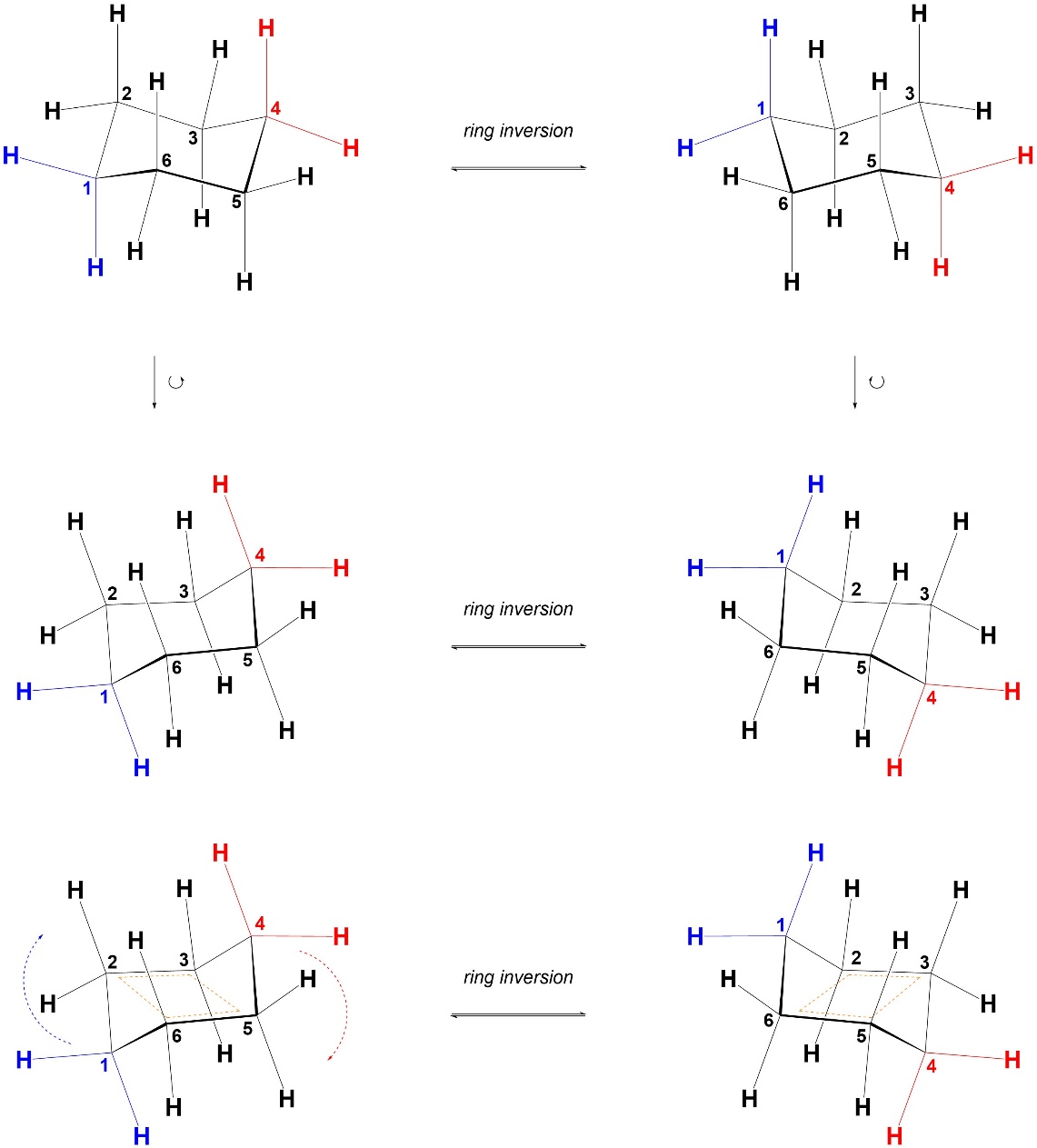
Figure 3.33 – Alternate Visualization of Chairs for Ring Inversion.

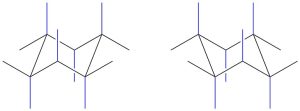
This works well for ring inversions in this text. However, it is important to remember that there are always multiple ways of drawing any chair conformation depending on the perspective chosen. The following is for demonstrative purposes only. For example, all of these are valid depictions of the same chair conformation of the same molecule (Figure 3.34). The other chair conformation also has 12 possible perspectives. As a result, it is possible for drawings in some sources to become very confusing; with 12 perspectives for one chair and 12 perspectives for the other there are theoretically 144 ways to show the relationship between any two chairs.

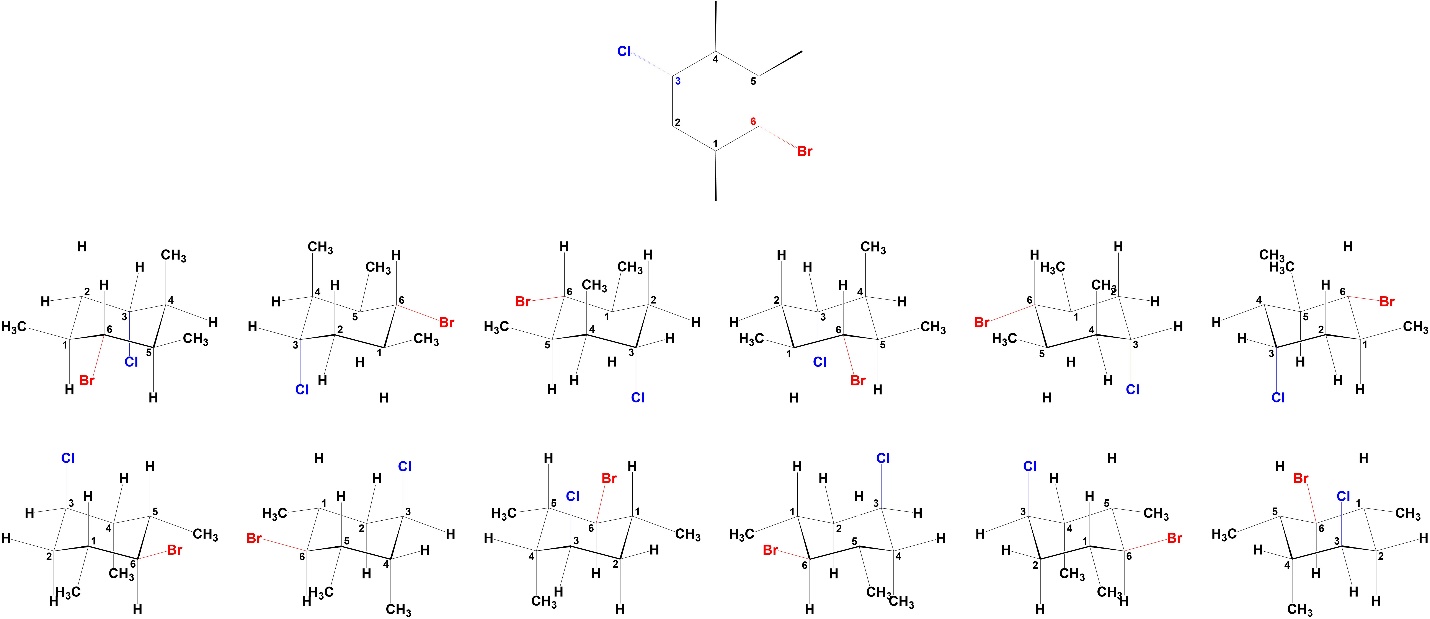
Figure 3.34 – Multiple Perspectives of the Same Chair Conformation for a Molecule.

Drawing all twelve perspectives is more tedious than challenging and would not be expected at an introductory level. However, it is important understand that multiple perspectives are possible, especially when classifying the relationship between two structures/drawings (see Section 4.2.4).

3.6.4.3. How to Draw Chair Conformers

There are a variety of ways to draw chair conformations. Most of these suggest drawing bonds one at a time and rely on the illustrator being a moderately talented artist. While these approaches work for some, an alternate is suggested: “My Way”.

• Draw a horizontally stretched out “M”.

• Beneath this and offset slightly to the left or right, draw a horizontally stretched out “W”.

• Connect the two end pairs of vertices (not the pair in the middle).

• Add axial groups by drawing vertical lines from each vertex.

• Add the remaining two equatorial groups by drawing two lines roughly parallel to the connecting lines (from Step 3).

Remember that leaving the end of the lines blank means that there is a CH₃ (methyl) there, so explicitly writing in all groups is suggested to avoid accidentally methylating the ring.

If the hydrogens are not desired in the final drawing erase lines to them only after adding in all of the other groups. This helps to avoid issues where substituents are ambiguously drawn.

3.6.4.4. How to Actually Do the Ring Inversion

Many students of introductory organic chemistry use molecular model kits to help understand the three-dimensional shapes of molecules. It is possible to quickly use a molecular model to show how ring inversion (chair-flip) occurs. Being able to do this can help some individuals more easily recognize, generate, and/or draw the two chair conformations for a molecule.

1. Build a molecular model of a chair conformation for the molecule. Which of the two is made does not matter.

2. Rotate the entire molecule so that there is an obvious set of four carbons from the ring in a plane (see Figure 3.33). Which four carbons are in the plane does not matter, as long as it is consistent from here.

3. Grab the carbon below the plane. Rotate the bonds so that this carbon is now above the plane (the same amount “above” as it was “below” before). Try not to move the other carbons in the ring. As the carbon is raised the model passes through the half-chair and twist-boat conformations. It is now in a boat conformation.

4. Grab the carbon that was originally above the plane. Rotate the bonds so that this carbon is now below the plane (the same amount “below” as it was “above” before). Try not to move the other carbons in the ring. As the carbon is lowered the model passes through the other twist-boat and half-chair conformations. It is now in the other chair conformation.

Analysis of conformations other than chairs is beyond the scope of this text. However, being able to see them with a model may clarify the process of ring inversion.

3.6.4.5. Substituent Effects on Conformer Distribution – 1,3-Diaxial Interactions and A-Values

Chair conformations of cyclohexane have no angle strain and no torsional strain along any C-C bond (see Section 3.6.4.). However, there is a different potential source of strain for these conformations (Figure 3.35).

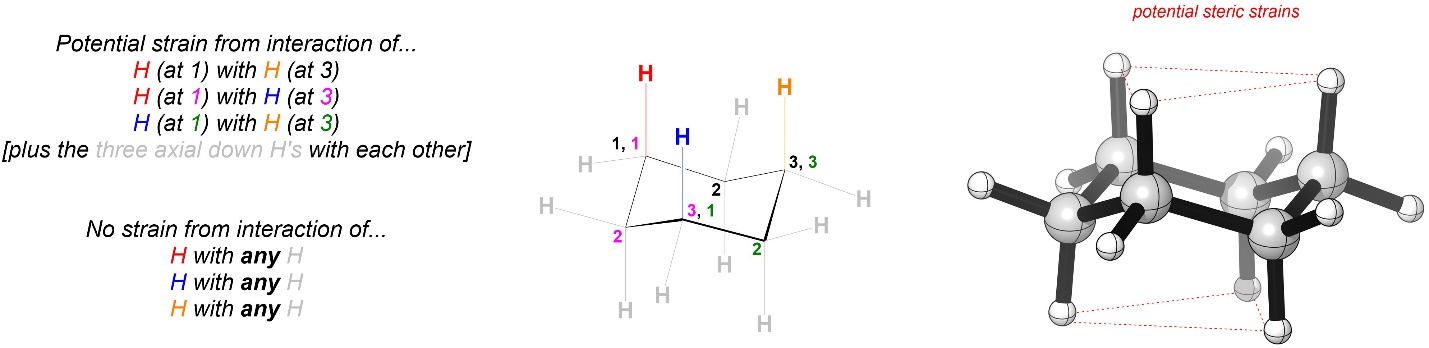
Figure 3.35 – Highlighted 1,3-Diaxial Interactions as Potential Sources of Strain.

This type of interaction is called a 1,3-diaxial interaction; if arbitrarily numbered, the axial groups at positions 1 and 3 experience strain from being close to each other. The three axial groups pointing up from the ring interact with each other, and the three axial groups pointing down from the ring interact with each other (not highlighted). Because all groups are very small in the case above there is technically no strain from 1,3-diaxial interactions; the hydrogens’ electron clouds are too small to get too close to each other. However, when comparing the strains in the two conformations it is best to list all potential interactions and then compare the two.

In cyclohexane the interactions experienced in the two conformations are identical (Figure 3.36). As a result, the two chair conformations are equal in energy. In a pure sample of cyclohexane at equilibrium for every molecule that is in the left chair conformation there will be another molecule in the right chair conformation.

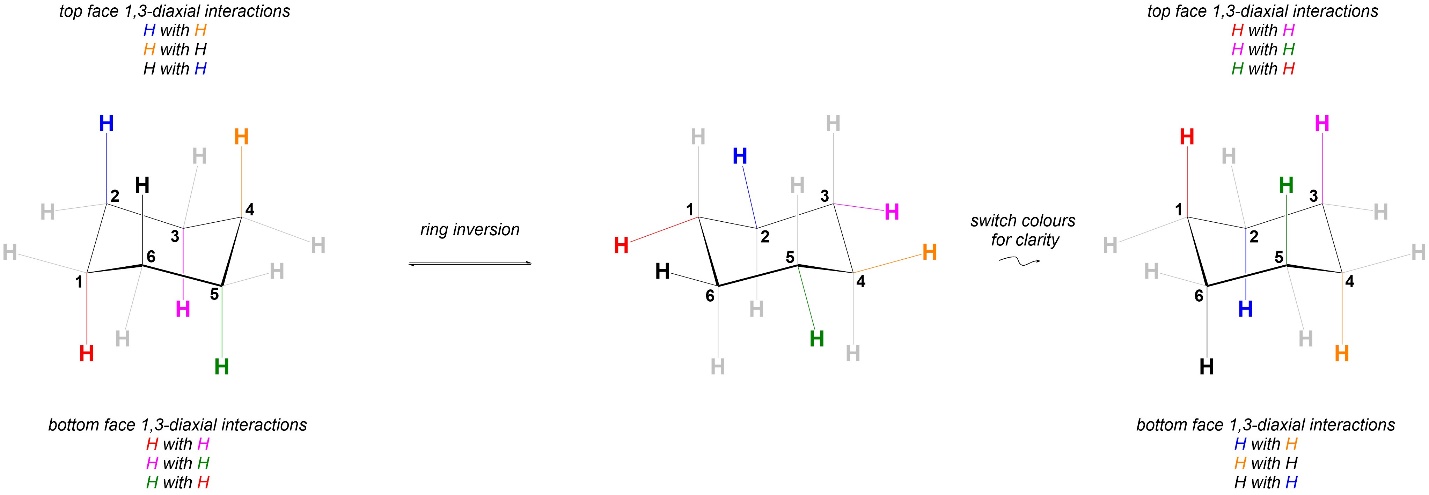
Figure 3.36 – Comparison of 1,3-Diaxial Interactions in Chair Conformations of Cyclohexane.

Once substituents are added this is not necessarily true anymore. The strains experienced in the two chair conformations of methylcyclohexane are different (Figure 3.37). As a result, the two chair conformations are NOT equal in energy. The conformation on the left is higher in energy than the one on the right; the steric strain experienced by the conformation on the left is higher than that on the right. In a pure sample of methylcyclohexane at equilibrium for every molecule that is in the left chair conformation there will be more than one molecule in the right chair conformation.

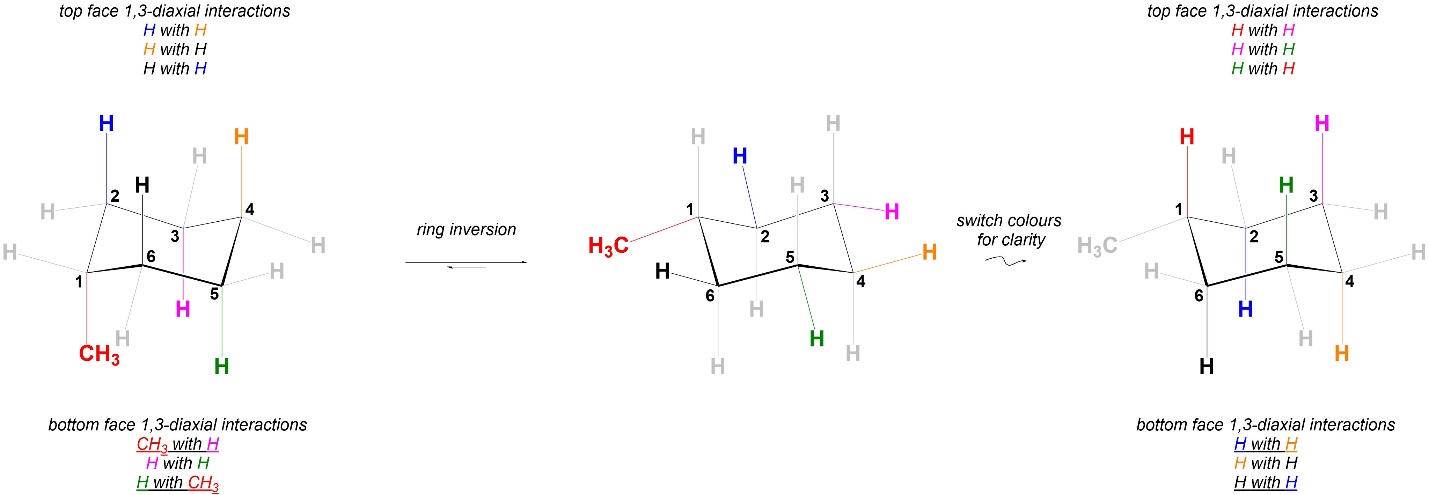
Figure 3.37 – Comparison of 1,3-Diaxial Interactions in Chair Conformations of Methylcyclohexane.

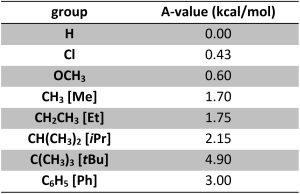
Substituents prefer to be equatorial to avoid steric train. It is possible to measure the amount of each chair conformation at equilibrium. Using this, an A-value (Table 3.1) can be calculated as a measure of how much energy is saved by having the substituent be equatorial. At an introductory level memorizing and using exact A-values is not important. Instead, the trend is important: the degree to which being equatorial is favoured is GENERALLY proportional to size (the bigger the group, the more it wants to be equatorial). There are exceptions but understanding these requires too deep an analysis.

Table 3.1 – Select A-Values for Common Substituents (at 298K).

When there are multiple substituents on the ring the situation becomes more complex. The two isomers (see Section 4.2) of 1,4-dimethylcyclohexane each have two chair conformations (Figure 3.38).

Figure 3.38 – Two Isomers of 1,4-Dimethylcyclohexane.

First, consider the isomer on the left. As a result of where the methyls are and them both being on the same side of the ring, in each chair conformation there is one methyl axial and one methyl equatorial (Figure 3.39).

Figure 3.39 – Chair Conformations of cis-1,4-Dimethylcyclohexane.

Comparing the 1,3-diaxial interactions in the two conformations, the two have exactly the same steric strains in them (Figure 3.40). As a result the two chair conformations are equal in energy.

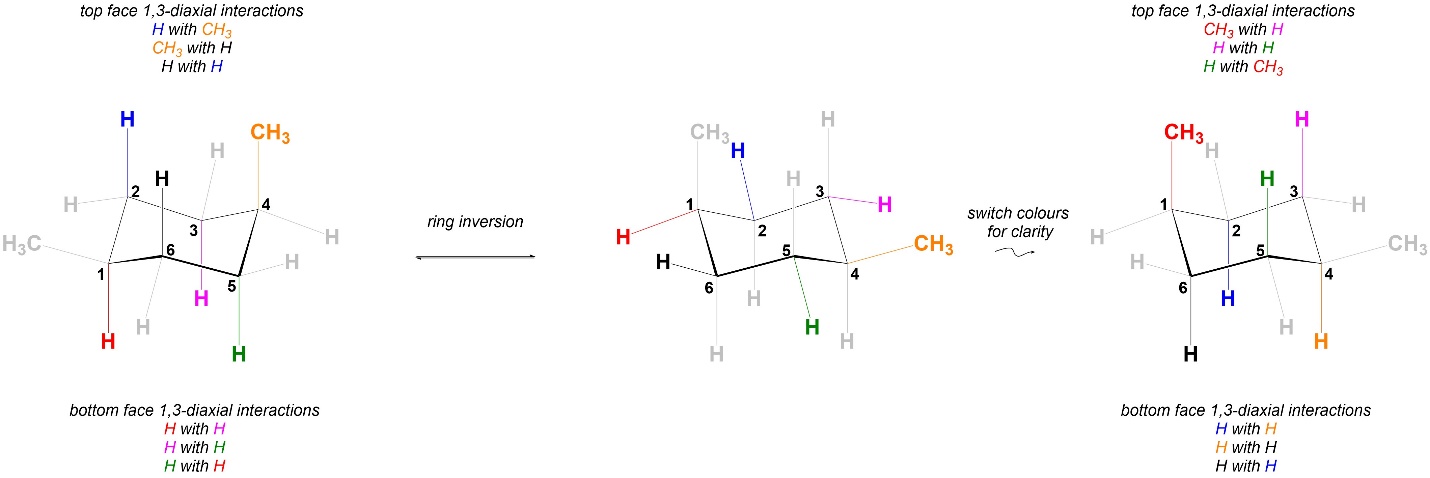
Figure 3.40 – Comparison of 1,3-Diaxial Interactions in Chair Conformations of cis-1,4-Dimethylcyclohexane.

Now, consider the isomer on the right. As a result of where the methyls are and them being on opposite sides of the ring, in one chair conformation there are two methyl groups axial and in the other there are two methyl groups equatorial (Figure 3.41).

Figure 3.41 – Chair Conformations of trans-1,4-Dimethylcyclohexane.

Comparing the 1,3-diaxial interactions in the two conformations, the two have different steric strains in them (Figure 3.42). As a result the two chair conformations are NOT equal in energy. The conformation on the left is more stable, and more of the molecules will be in it than the conformation on the right.

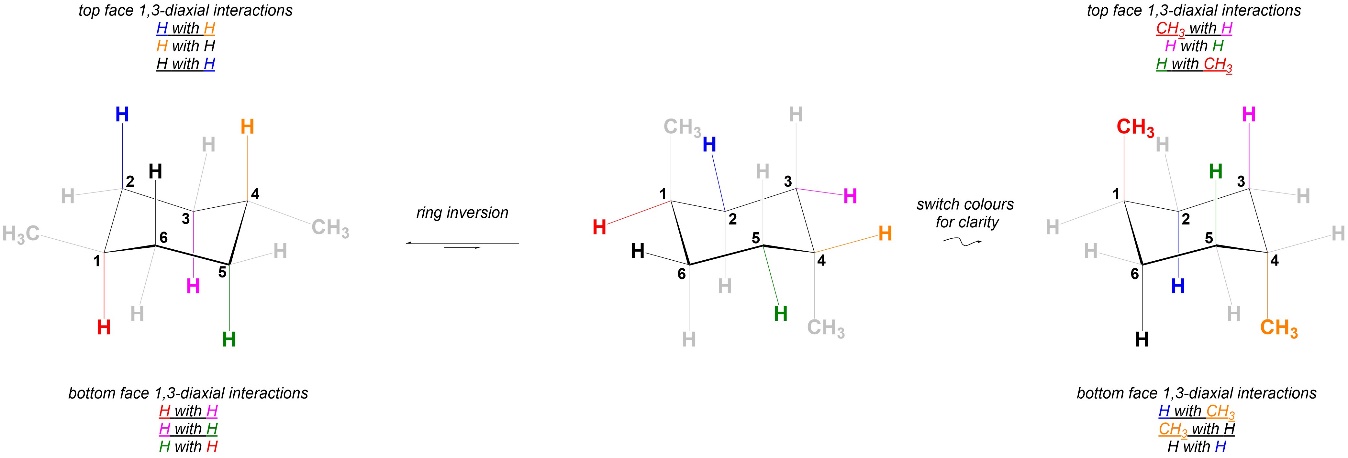
Figure 3.42 – Comparison of 1,3-Diaxial Interactions in Chair Conformations of trans-1,4-Dimethylcyclohexane.

The relative energies of chair conformations can change from where the groups are relative to each other in the structure. As with 1,4-dimethylcyclohexane, the two isomers (see Section 4.2) of 1,3-dimethylcyclohexane each have two chair conformations (Figure 3.43).

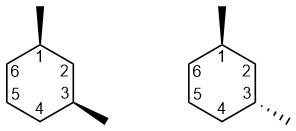
Figure 3.43 – Two Isomers of 1,3-Dimethylcyclohexane.

First, consider the isomer on the left. As a result of where the methyls are and them being on the same side of the ring, in one chair conformation there are two methyl groups axial and in the other there are two methyl groups equatorial (Figure 3.44).

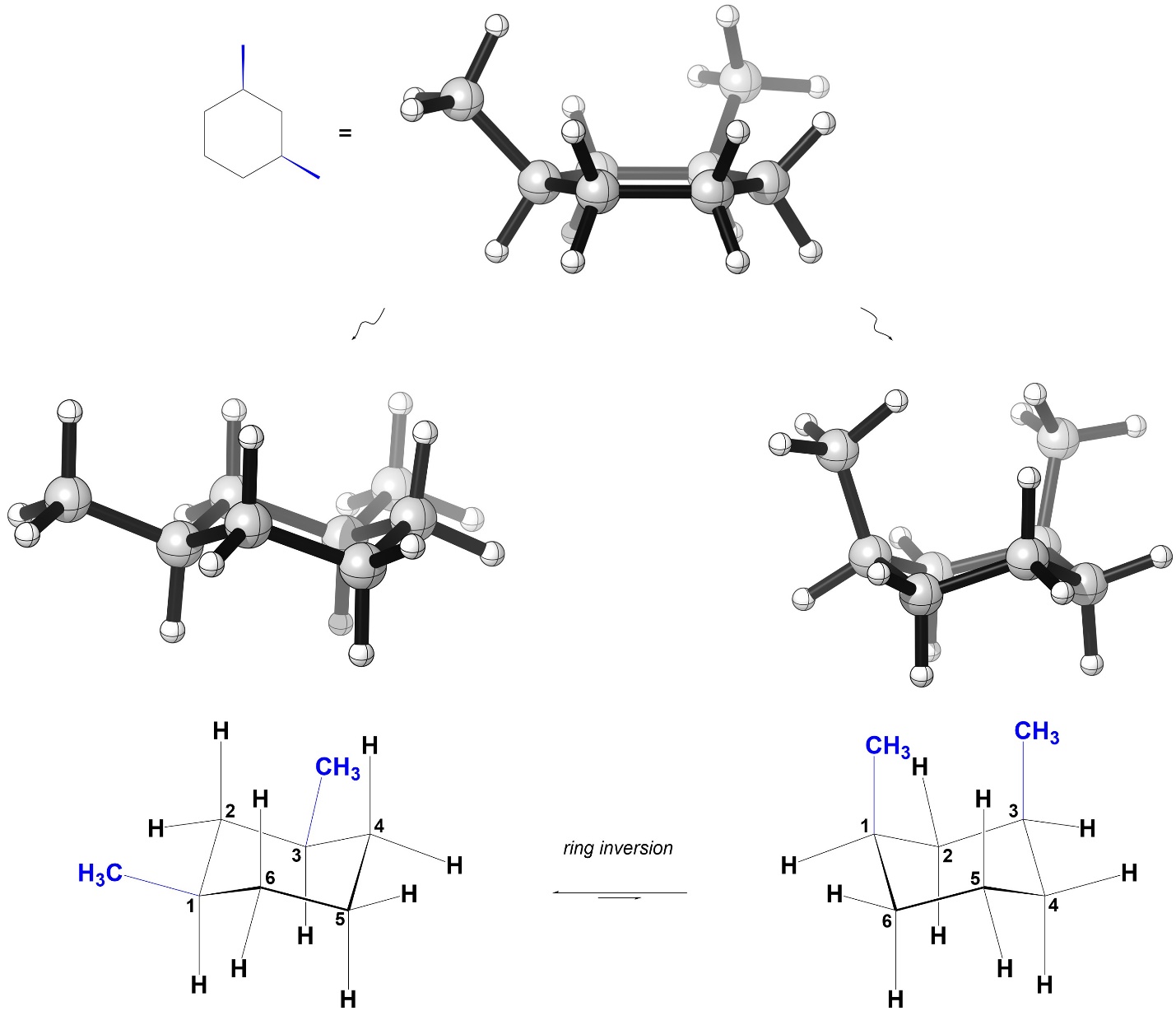
Figure 3.44 – Chair Conformations of cis-1,3-Dimethylcyclohexane.

Comparing the 1,3-diaxial interactions in the two conformations, the two have different steric strains in them (Figure 3.45). As a result the two chair conformations are NOT equal in energy. The conformation on the left is more stable, and more of the molecules will be in it than the conformation on the right. This is different from the equivalent 1,4-dimethylcyclohexane isomer (with both methyls on the same side of the ring; Figures 3.39 and 3.40) but is similar to the other isomer (Figures 3.41 and 3.42).

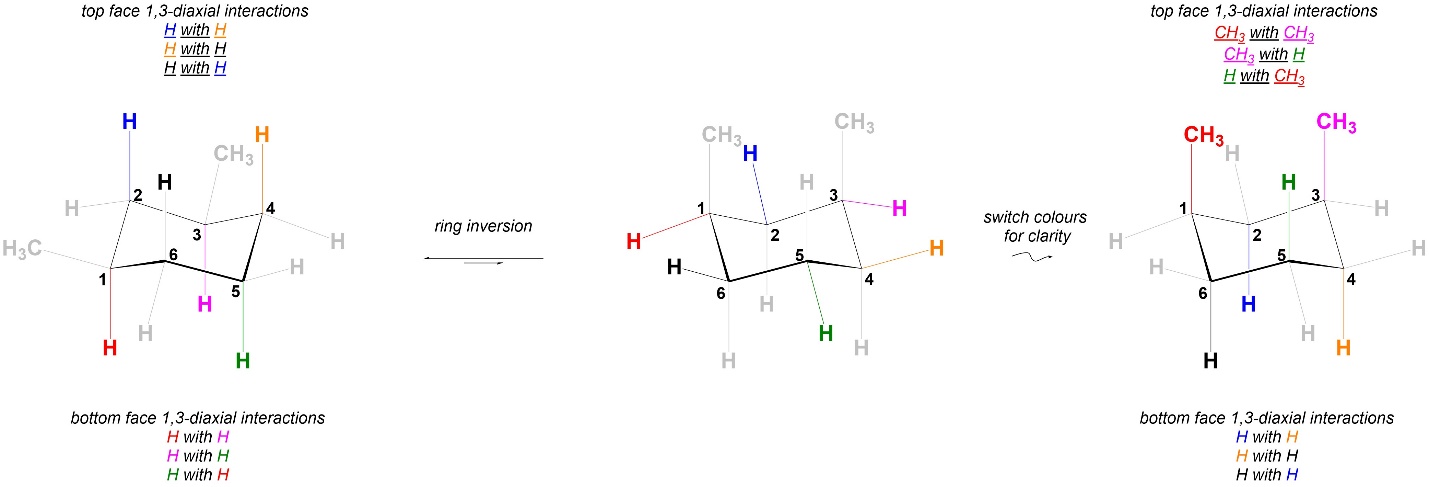
Figure 3.45 – Comparison of 1,3-Diaxial Interactions in Chair Conformations of cis-1,3-Dimethylcyclohexane.

Now, consider the isomer on the right. As a result of where the methyls are and them being on opposite sides of the ring, in each chair conformation there is one methyl axial and one methyl equatorial (Figure 3.46).

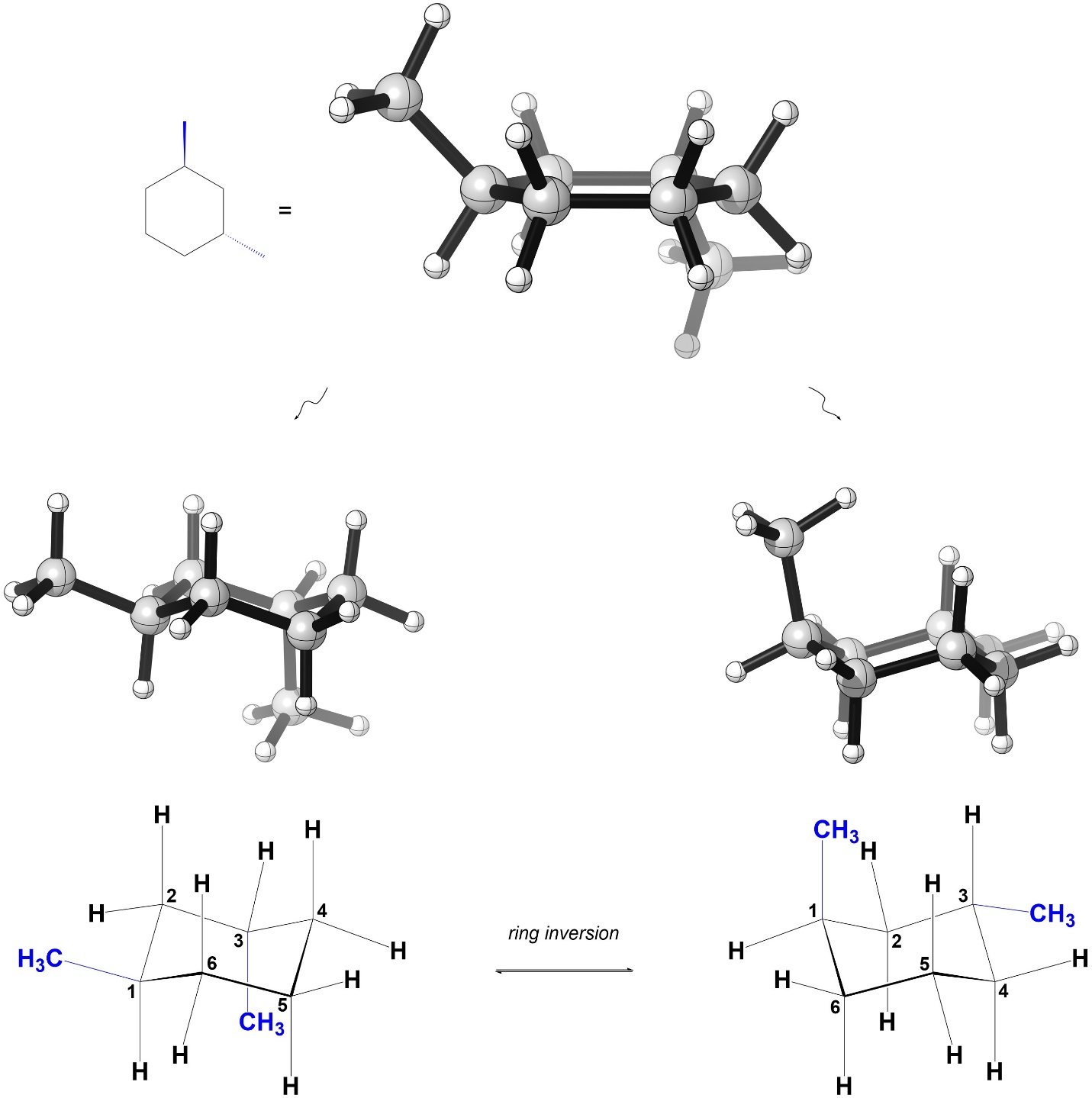
Figure 3.46 – Chair Conformations of trans-1,3-Dimethylcyclohexane.

Comparing the 1,3-diaxial interactions in the two conformations, the two have exactly the same steric strains in them (Figure 3.47). As a result the two chair conformations are equal in energy. This is different from the equivalent 1,4-dimethylcyclohexane isomer (with the methyls on opposite sides of the ring; Figures 3.41 and 3.42) but is similar to the other isomer (Figures 3.39 and 3.40).

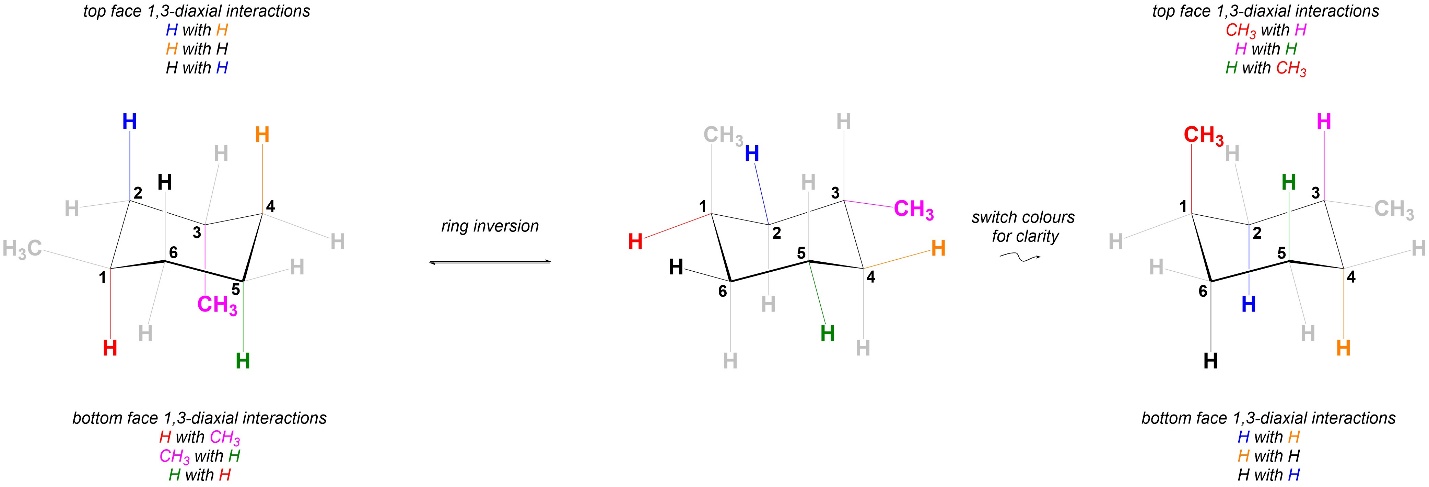
Figure 3.47 – Comparison of 1,3-Diaxial Interactions in Chair Conformations of trans-1,3-Dimethylcyclohexane.

A small change led to a completely different outcome for the relative energies of chair conformations (Figure 3.48). This highlights the necessity of analyzing 6-membered rings carefully in all cases. The approach is always the same: both chair conformations are analyzed in terms of their 1,3-diaxial interactions and then whether the two conformations are equally stable or whether one conformer is preferred can be determined.

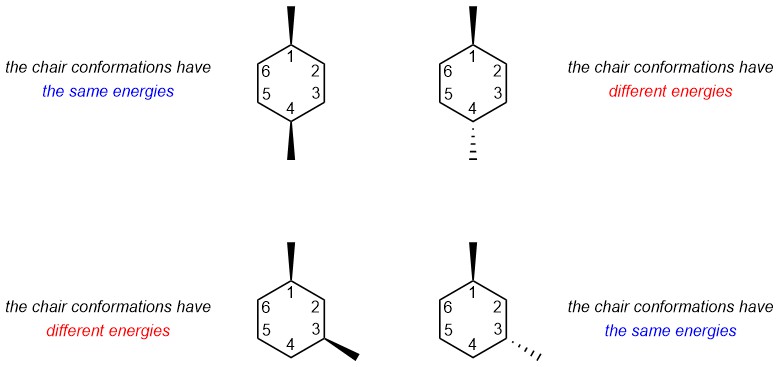
Figure 3.48 – Comparison Highlighting the Effects of Relative Group Positioning on Energies of Chair Conformations for Isomers of 1,4-Dimethylcyclohexane and 1,3-Dimethylcyclohexane.