3.3. Dihedral/Torsion Angles

The most familiar types of angles are those defined by three points (i.e. ∠ABC). However, when discussing angles between substituents in conformations the angle is defined by four points (i.e. ∠ABCD). For example, the angle of 0° shown above (Figure 3.3) could be described as ∠HCCH. A dihedral angle (sometimes called a torsion angle) is the angle between the two planes formed by the four groups (Figure 3.4). While the technical definition is useful, typically it is easier to simply view the Newman Projection and visualize the angle as degrees in a circle.

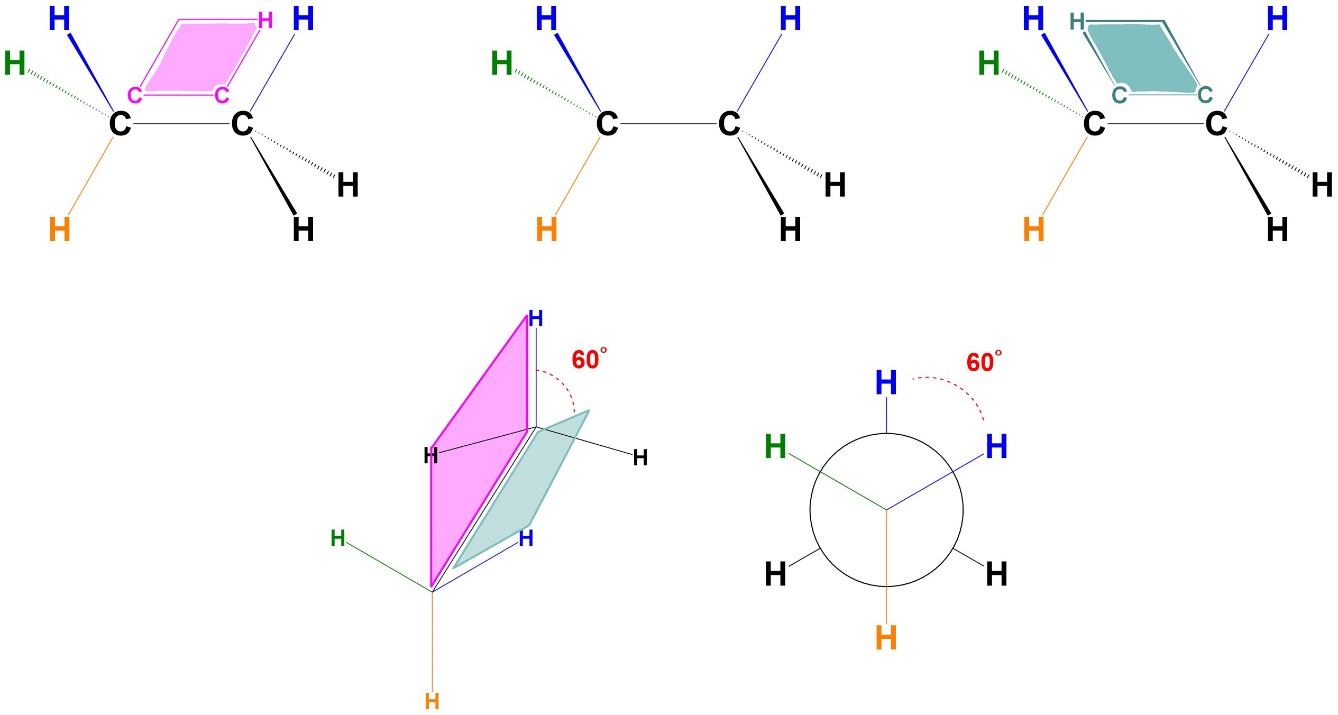
Figure 3.4 – Visualization of Dihedral Angles.

There is one important caveat for dihedral angles: the four points (atoms) must be directly connected in a row. The angle between two arbitrarily defined planes can be determined, but it is not a dihedral angle and is not usually useful to know.