"

6. Percentiles and Quartiles

The concept of percentile[1] applies to either a data set (sample, as represented by a histogram — a discrete distribution) or to a continuous distribution (which represents a population) as shown in Figure 6.1.

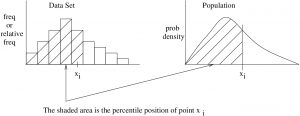
Figure 6.1: The concept of percentile applies to either a data set or to a continuous distribution.

The percentile position of the data point x_i, denoted here by P(x_{i}), is the percentage of the area under the curve up to the point x_{i}. Notation warning : Do not confuse percentile and probability, we use P to denote both!! (They are related though.)

To determine the percentile position for x_{i} from a normal distribution of values, convert x_{i} to z_{i} via the z-transformation, determine the area under the standard normal curve up to z_{i} and multiply by 100. We have, therefore, already seen how to compute P(x_{i}) given x_{i} or how to compute x_{i} for a given percentile P. See Case 5 in Section 5.3 and remember how to use the Standard Normal Distribution Table forward and backwards.

  1. This percentile stuff is all about cumulative frequency or (thinking about probabilities) cumulative relative frequencies. The corresponding probability functions are called Cumulative Distribution Functions or CDFs. You will encounter CDFs in SPSS; they are mentioned later in this chapter. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book