7. The Central Limit Theorem
7.1 Using the Normal Distribution to Approximate the Binomial Distribution
Recall the definitions: ![]() = probability of success,
= probability of success, ![]() = probability of failure and
= probability of failure and ![]() = sample size. When
= sample size. When ![]() and
and ![]() then the normal distribution is very close, numerically, to the binomial distribution.
then the normal distribution is very close, numerically, to the binomial distribution.
Using the histogram way of drawing the binomial distribution, a good fit looks like that shown in Figure 7.1.
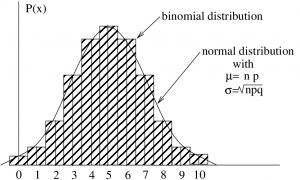
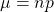 and standard deviation
and standard deviation 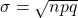 is a good fit to the binomial distribution with the same mean and standard deviation as long as
is a good fit to the binomial distribution with the same mean and standard deviation as long as 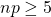 and
and 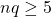 .
.A couple of things to note about this approximation:
- Although the values of the normal and the binomial distributions match well at
 equal to integer values when
equal to integer values when 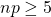 and
and 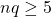 , the areas match not as well. A “correction for continuity” can be used to better make the areas match but we won’t be worrying about such fine details in our studies.
, the areas match not as well. A “correction for continuity” can be used to better make the areas match but we won’t be worrying about such fine details in our studies. - We will use the normal approximation to the binomial make inferences on proportions. In that case
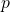 , the probability of success will represent a proportion in a population.
, the probability of success will represent a proportion in a population.

