4.1 Probability

Gordon E. Sarty

4. Probability and the Binomial Distributions

4.1 Probability

The basic definition of probability is a ratio of things you can count (a ratio of their frequencies) :

(4.1) $\begin{equation*} P(E) = \frac{n(E)}{n(S)} \end{equation*}$

where

$P(E)$ is the probability that event $E$ happens,
$n(E)$ is the number of ways $E$ can happen and
$n(S)$ is the total number of outcomes (all possibilities).

Example 4.1 : What is the probability of drawing a queen from a deck of cards :

$P(E) = \frac{4}{52} = 0.077 \mbox{\ \ \ (7.7\% if we were to express the result in percentages)}$

▢

To use $P(E)$ mathematically we set

$0 \leq P(E) \leq 1$

Where, probability-wise:

0 means $E$ definitely will not occur, and
1 means $E$ definitely will occur.

This is a method we can use instead of using percent. To compute probabilities, we first need to know how to count.

Fundamental Counting Rule

Say you have n events in order, and for event $i$ there are $k_{i}$ ways for it to happen. Then the number of ways for the $n$ events to play out is :

$k_1 \cdot k_2 \cdot k_3 \hdots k_n = \prod_{i=1}^{n} k_i$

(The giant pi symbolizes a multiplication convention in the same way that a giant sigma symbolizes a summation convention as described in Section 1.3.)

Example 4.2 How many combinations are there on a lock with 3 numbers?

Lay out the events as : $k_{1}=10$ , $k_{2}=10$ , and $k_{3}=10$ . Note that each number can be anything from 0 to 9 giving 10 possibilities ( $k_{i} = 10$ ) for each event. So the number of possible lock combinations is

$k_1 k_2 k_3 = 10 \cdot 10 \cdot 10 = 10^3 = 1000$

Note that you could have guessed this because the combination range from 000 to 999 — counting in base 10.

▢

Example 4.3 Suppose that a hardware store can produce paints with the following qualities :

Colour : red, blue, white, black, green, brown, yellow (7 colours)

Type : latex, oil (2 types)

Texture : flat, semigloss, high-gloss (3 textures)

Use : indoor, outdoor (2 uses)

How many ways are there to combine these qualities to produce a can of paint?

Answer : From the above list $k_{1}=7, k_{2}=2, k_{3}=3, k_{4}=2$ and the number of possible paint kinds is:

$7 \cdot 2 \cdot 3 \cdot 2 = 84$

▢

Applications of the Fundamental Counting Rule

We are interested in applying the fundamental counting rule to two special, important cases :

Permutations.
Combinations.

Let’s define each one.

Permutations.

The number of ways, or permutations, of selecting $r$ objects from a collection or $n$ objects, while keeping track of the order of selection is ^[1]

${}_{n}P_{r} = \frac{n!}{(n-r)!}$

This formula follows from the fundamental counting rule. With $n$ objects there are $k_{1} = n$ ways to select the first object. After selecting the first object there are $n-1$ ways to choose the second object so $k_{2} = n-1$ , etc. up to $k_{r} = n - r + 1$ :

${}_nP_r = (n)(n-1)(n-2) \hdots (n-r+1)$

$= \frac{(n)(n-1) \hdots (2)(1)}{(n-r)(n-r-1) \hdots (2)(1)}$

Example 4.4 : How many ways are there to choose 5 numbered balls from a bucket of 25 to make a lottery number?

Answer : $25 \cdot 24 \cdot 23 \cdot 22 \cdot 21 = 6,375,600$ possibilities.

▢

2. Combinations.

The number of ways of selecting $x$ objects from a collection of $n$ objects without caring about the order is :

${}_nC_x = \frac{n!}{(n-x)!x!} = \frac{{}_nP_x}{x!} = \left( \begin{array}{c} n \\ x \end{array}\right)$

That last symbol $\left( \begin{array}{c} n \\ x \end{array}\right)$ is colloquially called “ $n$ choose $x$ ”. The second last expression demonstrates the application of the fundamental counting principal, it says

$\left( \begin{array}{c} n \\ x \end{array}\right) = \frac{(n)(n-1) \hdots (n-x-1)}{x!}$

where $x!$ is just the number of ways of arranging $x$ objects while caring about the order, $x! = {}_{x}P_{x}$ .

As a practical matter, never try to compute $n!$ It will usually be unimaginably big. Use the formula that directly shows the fundamental counting rule as shown in the following example.

Example 4.5 : How many ways are there to select 10 balls from a bucket of 100?

Answer :

$\left( \begin{array}{c} 100 \\ 10 \end{array} \right) = \frac{100 \cdot 99 \cdot 98 \cdot 97 \cdot 96 \cdot 95 \cdot 94 \cdot 93 \cdot 92 \cdot 91} {10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ = \frac{6.2815651 \times 10^{19}}{3,628,800} = \underline{17.3 \times 10^{12}}$

▢

The symbol $\left( \begin{array}{c} n \\ x \end{array}\right)$ is also known as the binomial coefficient because it shows up in algebra when you expand expressions of the form $(x+y)^{n}$ . For example^[2]

$(x+y)^n = x^2 + 2xy + y^2$

$\begin{eqnarray*} (x+y)^3 &=& \left( \begin{array}{c} 3\\0 \end{array} \right)x^3 + \left( \begin{array}{c} 3\\1 \end{array} \right)x^2y + \left( \begin{array}{c} 3\\2 \end{array} \right) xy^2 + \left( \begin{array}{c} 3\\3 \end{array} \right) y^3 \\ &=& x^3 + 3x^2y + 3xy^2 + y^3 \end{eqnarray*}$

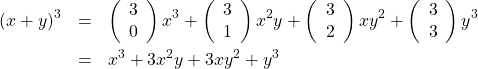
The binomial coefficients can be quickly computed using Pascal’s triangle :

$\begin{array}{ccccccccccccccc} &&&&&&&&&&&&&& n = \\ &&&&&& 1 &&&&&&&& 0 \\ &&&&& 1 && 1 &&&&&&& 1 \\ &&&& 1 && 2 && 1 &&&&&& 2 \\ &&& 1 && 3 && 3 && 1 &&&&& 3 \\ && 1 && 4 && 6 && 4 && 1 &&&& 4 \\ & 1 && 5 && 10 && 10 && 5 && 1 &&& 5 \\ 1 && 6 && 15 && 20 && 15 && 6 && 1 && 6 \\ &&&&&& \mbox{etc.} \end{array}$

Referring to Pascal’s triangle we can quickly write

$(x+y)^6 = x^6 + 6x^5y + 15x^4y^2 + 20x^3y^3 + 15x^2y^4 + 6xy^5 + y^6$

for example.

Recall that the definition of factorial follows $5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$ etc. ↵
You don't need this algebra for this statistics course. It's just interesting. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Share This Book