10. Comparing Two Population Means
10.2 Confidence Interval for Difference of Means (Large Samples)
Swapping the roles of sample and population in the sampling theory, we have the confidence interval corresponding to the hypothesis test of Section 10.1
![]()
where
![Rendered by QuickLaTeX.com \[E = z_{\cal C}\sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-e292d4e089d19b4ce07f3ea68ca8a542_l3.png)
Example 10.2 : Find the 95![]() confidence interval for the difference between the means for the data of Example 10.1.
confidence interval for the difference between the means for the data of Example 10.1.
Solution : First, recall our data :
![]() ,
, ![]() ,
, ![]()
![]() .
. ![]() ,
, ![]()
From the t Distribution Table, look up the ![]() for the 95
for the 95![]() confidence interval:
confidence interval: ![]() . Then compute:
. Then compute:
![]()
and
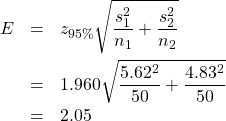
so
![]()
or
![]()
with 95![]() confidence. Notice that it is also correct to write
confidence. Notice that it is also correct to write ![]() with 95
with 95![]() confidence.
confidence.
▢
This is a good point to make an important observation. A two-tailed hypothesis test at a given ![]() is complementary to a confidence interval of
is complementary to a confidence interval of ![]() in the sense that if 0 is in the confidence interval then the complementary hypothesis test will not reject
in the sense that if 0 is in the confidence interval then the complementary hypothesis test will not reject ![]() .
.
Let’s illustrate this principle with a one-sample ![]() -test under
-test under ![]() . (We need
. (We need ![]() for this principle to work.) Look at the two possible outcomes :
for this principle to work.) Look at the two possible outcomes :
Case 1 : 0 in the confidence interval, fail to reject ![]() . In the hypothesis test you would find :
. In the hypothesis test you would find :
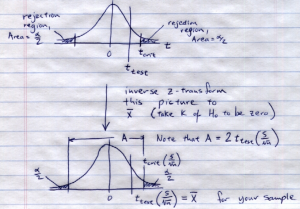
In the confidence interval calculation you would find:
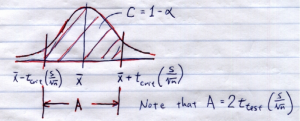
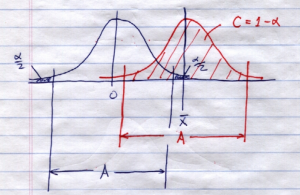
Putting the two pictures together gives:
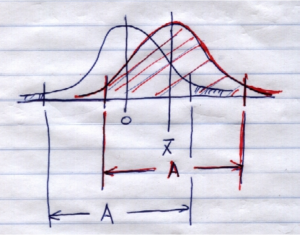
See, ![]() is in the confidence interval if ¯
is in the confidence interval if ¯![]() is not in the rejection region. The red distribution that defines the confidence interval is just the blue (identical) distribution slid over from
is not in the rejection region. The red distribution that defines the confidence interval is just the blue (identical) distribution slid over from ![]() to
to ![]() . The distance
. The distance ![]() is the same because
is the same because ![]() .
.
Case 2 : 0 not in the confidence interval, reject ![]() . In this case the combined picture looks like:
. In this case the combined picture looks like:
Before we can consider the independent sample ![]() -test, we need a tool for checking what the variances of the populations are. The formula for the
-test, we need a tool for checking what the variances of the populations are. The formula for the ![]() test statistic will depend on whether the two variances are the same or not. So let’s take a look at comparing population variances.
test statistic will depend on whether the two variances are the same or not. So let’s take a look at comparing population variances.

