16. Non-parametric Tests

16.4 Two Sample Wilcoxon Rank Sum Test (Mann-Whitney U Test)

This test is an alternative to the two sample t-test. The test assumes that the population of differences has a symmetric distribution and tests the following hypothesis pair :

H_{0}: The means of the two populations are the same.
H_{1}: The means of the two populations are the different.

or

H_{0}: \mu_{1} = \mu_{2}
H_{1}: \mu_{1} \neq \mu_{2}

which is exactly the hypothesis tested by the t-test. The samples are independent (no pairs) and, although this test compares means (parameters) and not medians, it does not use the values of the means to do the comparison — therefore this is a non-parametric test. It is based on a binomial distribution.

The test statistic is

    \[z_{\mbox{test}} = \frac{R- \mu_{R}}{\sigma_{R}}\]

where

    \[ \mu_{R} & = & \frac{n_{1}(n_{1}+n_{2}+1)}{2} \]

    \[ \sigma_{R} & = & \sqrt{\frac{n_{1} n_{2}(n_{1}+n_{2}+1)}{12} } \]

    \[ R & = & \mbox{sum of ranks for the smaller sample } (n_{1}) \]

    \[ n_{1} & = & \mbox{smaller sample size} \]

    \[ n_{2} & = & \mbox{larger sample size} \]

Also we need n_{1}, n_{2} \geq 10 in order for the z distribution to be a good fit to the binomial distribution. This is our first non-parametric test that uses rank. Let’s follow an example to see how it all works.

 

Example 16.6 : Given the following obstacle course times, is the army or marines significantly faster?

Army: 15 18 16 17 13 22 24 17 19 21 26 28
Marines: 14 9 16 19 10 12 11 8 15 18 25

Solution.

0. Data reduction.

We need to assign group 1 to the smaller sample. So let

group 1 = Marines (M) and n_{1} = 11
group 2 = Army (A) and n_{2} = 12

We don’t need to compute the means to compare them but just out of curiosity we note that \overline{x}_{1} = 14.27 and \overline{x}_{2} = 19.67 so if there is a significant difference between the means then the marines are faster.

This is our first rank test so we need to apply the methods of Section 16.1. For this test, we rank the combined data :

Group Time Rank Count
M 8 1 1
M 9 2 2
M 10 3 3
M 11 4 4
M 12 5 5
A 13 6 6
M 14 7 7
M 15 8.5 8
A 15 8.5 9
M 16 10.5 10
A 16 10.5 11
A 17 12.5 12
A 17 12.5 13
M 18 14.5 14
A 18 14.5 15
M 19 16.5 16
A 19 16.5 17
A 21 18 18
A 22 19 19
A 24 20 20
M 25 21 21
A 26 22 22
A 28 23 23

Notice how the last Count column is useful for assigning ranks to the ties. We have also drawn boxes around the marines because they are the smaller group and we need the sum of the ranks of the smaller group :

    \[ R = 1 + 2 + 3 + 4 + 5 + 7 + 8.5 + 10.5 + 14.5 + 16.5 + 21 = 93 \]

1. Hypothesis.

    \begin{eqnarray*} H_{0} &:& \mu_{1} = \mu_{2} \\ H_{1} &:& \mu_{1} \neq \mu_{2} \end{eqnarray*}

2. Critical statistic.

Using the last (z) line in the t Distribution Table with \alpha = 0.05 for the two-tailed test we find

    \[ z_{\mbox{crit}} = \pm 1.960 \]

3. Test statistic.

We already have R = 93. Now compute:

    \begin{eqnarray*} \mu_{R} & = & \frac{n_{1}(n_{1} + n_{2} + 1)}{2} \\ & = & \frac{11(11 + 12 + 1)}{2} \\ & = & 132 \\ \\ \sigma_{R} & = & \sqrt{\frac{n_{1} n_{2} (n_{1} + n_{2} + 1) }{12}} \\ & = & \sqrt{\frac{(11) (12) (11 + 12 + 1) }{12}} \\ & = & 16.2 \\ \\ z_{\mbox{test}} & = & \frac{R - \mu_{R}}{\sigma_{R}} \\ & = & \frac{93-132}{16.2}\\ & = & -2.41 \end{eqnarray*}

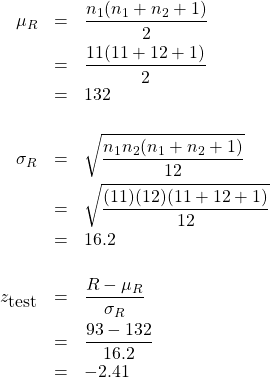
4. Decision.

Reject H_{0}.

5. Interpretation. The marines are significantly faster.

▢

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book