5. The Normal Distributions
5.2 **The Normal Distribution as a Limit of Binomial Distributions
The results of the derivation given here may be used to understand the origin of the Normal Distribution as a limit of Binomial Distributions[1]. A mathematical “trick” using logarithmic differentiation will be used.
First, recall the definition of the Binomial Distribution[2] as
(5.2) ![]()
where ![]() is the probability of success,
is the probability of success, ![]() is probability of failure and
is probability of failure and
(5.3) ![]()
is the binomial coefficient that counts the number of ways to select ![]() items from
items from ![]() items without caring about the order of selection. Here
items without caring about the order of selection. Here ![]() is a discrete variable,
is a discrete variable, ![]() , with
, with ![]() .
.
The trick is to find a way to deal with the fact that ![]() (
(![]() is a discrete variable) for the Binomial Distribution and
is a discrete variable) for the Binomial Distribution and ![]() (
(![]() is a continuous variable) for the Normal Distribution[3] In other words as we let
is a continuous variable) for the Normal Distribution[3] In other words as we let ![]() we need to come up with a way to let
we need to come up with a way to let ![]() shrink[4] so that a probability density limit (the Normal Distribution) is reached from a sequence of probability distributions (modified Binomial Distributions). So let
shrink[4] so that a probability density limit (the Normal Distribution) is reached from a sequence of probability distributions (modified Binomial Distributions). So let ![]() represent the Normal Distribution with mean
represent the Normal Distribution with mean ![]() and variance
and variance ![]() . We will show how
. We will show how ![]() where each Binomial Distribution
where each Binomial Distribution ![]() also has mean
also has mean ![]() and variance
and variance ![]() .
.
The heart of the trick is to notice[5] that
(5.4) ![]()
This is perfectly true for the density ![]() . The trick is to substitute the distribution
. The trick is to substitute the distribution ![]() for the density
for the density ![]() in the RHS of Equation (5.4) to get :
in the RHS of Equation (5.4) to get :
(5.5) ![]()
because ![]() . The trick is to now pretend that
. The trick is to now pretend that ![]() is a continuous function defined at all
is a continuous function defined at all ![]() ; we just don’t know what its values should be for non-integer
; we just don’t know what its values should be for non-integer ![]() . With such a “continuation” of
. With such a “continuation” of ![]() we can write[6]
we can write[6]
(..) 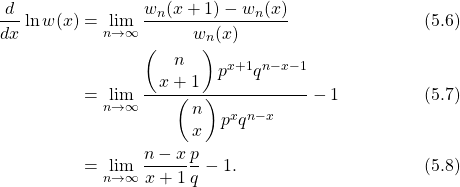
Equation (5.8) has no limit; it blows up as ![]() . We need to transform
. We need to transform ![]() in such a way to gain control on
in such a way to gain control on ![]() (getting it to shrink as
(getting it to shrink as ![]() ) and to get something that converges. To do that we introduce
) and to get something that converges. To do that we introduce ![]() and a new variable
and a new variable ![]() . With this transformation of variables, the chain rule gives
. With this transformation of variables, the chain rule gives
(5.9) ![]()
and the RHS of Equation (5.8) becomes, using ![]()
(..) 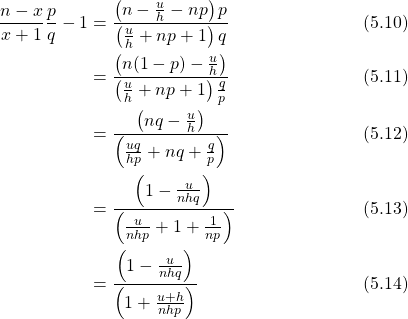
Using Equation (5.9), for the LHS, and Equation (5.14), for the RHS, Equation (5.8) becomes
(..) ![Rendered by QuickLaTeX.com \begin{align*} h \frac{d}{du} \ln w(u) & = \lim_{n \rightarrow \infty} \frac{1 - \frac{u}{nhq}}{1+\frac{u+h}{nhp}} - 1 \tag{5.15}\\ & = \lim_{n \rightarrow \infty} \left( 1 - \frac{u}{nhq} \right) \left[ 1 - \frac{u+h}{nhp} + \left( \frac{u+h}{nhp} \right)^{2} - \ldots \right] - 1 \tag{5.16}\\ & = \lim_{n \rightarrow \infty} -\frac{1}{np} - \frac{u}{nhq} - \frac{u}{nhp} + O\left(\frac{1}{n}\right) \tag{5.17}\\ & = \lim_{n \rightarrow \infty} -\frac{1}{np} - \frac{u}{nhpq} + O\left(\frac{1}{n}\right) \tag{5.18}\\ &= \lim_{n \rightarrow \infty} - \frac{u}{nhpq}. \tag{5.19} \end{align*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-94d34a95ab6a06da597162de5abd3ae3_l3.png)
where ![]() means terms that will go to zero as
means terms that will go to zero as ![]() , and we have used the relation
, and we have used the relation ![]() to get Equation (5.16}) and
to get Equation (5.16}) and ![]() to go from Equation (5.17) to Equation (5.18). Dividing both sides of Equation (5.19) by
to go from Equation (5.17) to Equation (5.18). Dividing both sides of Equation (5.19) by ![]() leaves
leaves
(5.20) ![]()
Our transformation, with its ![]() , has given us the exact control we need to keep the limit from disappearing or blowing up. Integrating Equation (5.20) gives
, has given us the exact control we need to keep the limit from disappearing or blowing up. Integrating Equation (5.20) gives
(5.21) ![]()
where ![]() is the a constant of integration. Switching back to the
is the a constant of integration. Switching back to the ![]() variable
variable
(..) ![Rendered by QuickLaTeX.com \begin{align*} w(x) & = C e^{-\frac{(h[x-\overline{x}])^{2}}{2pq}} \tag{5.22}\\ & = C e^{-\frac{(x-\overline{x})^{2}}{2npq}} \tag{5.23}\\ & = C e^{-\frac{(x-\overline{x})^{2}}{2\sigma^{2}}}. \tag{5.24} \end{align*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-95e94f780dab39f99dcb93c4789c959a_l3.png)
To evaluate the constant of integration, ![]() , we impose
, we impose ![]() because we want
because we want ![]() to be a probability distribution. So
to be a probability distribution. So
(5.25) ![]()
so
(5.26) ![]()
and
(5.27) ![]()
which is the Normal Distribution that approximates Binomial Distributions with the same mean and variance as ![]() gets large.
gets large.
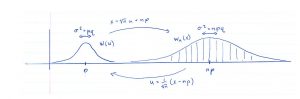
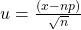 effectively shrinks the
effectively shrinks the  of the Binomial Distribution with mean
of the Binomial Distribution with mean 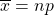 and variance
and variance 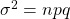 by pulling a continuous version
by pulling a continuous version  back to the constant Normal Distribution
back to the constant Normal Distribution 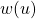 . Another way of thinking about it is that the transformation
. Another way of thinking about it is that the transformation 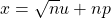 takes the fixed Normal Distribution
takes the fixed Normal Distribution 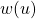 to the Normal Distribution
to the Normal Distribution 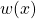 that provides a better and better approximation of
that provides a better and better approximation of  as
as 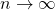 .
.You may be wondering why that transformation ![]() worked because it seems to have been pulled from the air. According to Lindsay & Margenau, it was Laplace who first used this transformation and derivation in 1812. What this transformation does is pull the Binomial Distribution
worked because it seems to have been pulled from the air. According to Lindsay & Margenau, it was Laplace who first used this transformation and derivation in 1812. What this transformation does is pull the Binomial Distribution ![]() back to have a mean of zero (by subtracting
back to have a mean of zero (by subtracting ![]() ) which keeps
) which keeps ![]() from running off to infinity and, more importantly, allows us to define a function
from running off to infinity and, more importantly, allows us to define a function ![]() with
with ![]() that has a constant variance of
that has a constant variance of ![]() that we can match to
that we can match to ![]() when we transform back to
when we transform back to ![]() at each
at each ![]() , see Figure 5.1. Looking at it the other way around, the Normal Distribution[7]
, see Figure 5.1. Looking at it the other way around, the Normal Distribution[7] ![]() with
with ![]() is an approximation for Binomial Distribution
is an approximation for Binomial Distribution ![]() that “asymptotically” approaches
that “asymptotically” approaches ![]() as
as ![]() .
.
This is not the only way to form a probability density limit from a sequence of Binomial distributions. It is one that gives a good approximation of the Binomial Distribution when ![]() is fairly small if the term
is fairly small if the term ![]() in Equation (5.18) becomes small quickly. If
in Equation (5.18) becomes small quickly. If ![]() is very small, this does not happen and another limit of Binomial Distributions that leads to the Poisson Distribution is more appropriate. When
is very small, this does not happen and another limit of Binomial Distributions that leads to the Poisson Distribution is more appropriate. When ![]() and
and ![]() are close to 0.5 or more generally when
are close to 0.5 or more generally when ![]() and
and ![]() then the Normal approximation is a good one. Either way, the density limit is a mathematical idealization, a convenience really, that is based on a discrete probability distribution that just summarizes the result of counting outcomes. Counting gives the foundation for probability theory.
then the Normal approximation is a good one. Either way, the density limit is a mathematical idealization, a convenience really, that is based on a discrete probability distribution that just summarizes the result of counting outcomes. Counting gives the foundation for probability theory.
- The formula for the Binomial Distribution was apparently derived by Newton according to: Lindsay RB, Margenau. Foundations of Physics. Dover, New York, 1957 (originally published 1936). For that claim, Lindsay & Margenau quote: von Mises R. Probability, Statistics, and Truth. Macmillan, New York, 1939 (originally published 1928). The derivation of the Normal Distribution presented here largely follows that given in Lindsay & Margenau's book. ↵
- In class we denoted the Binomial distribution as
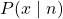 . Here we use
. Here we use 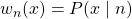 to avoid using too many P's and p's. ↵
to avoid using too many P's and p's. ↵ - Remember that the Normal Distribution is technically a probability density but we slur the use of the word distribution between probability distribution (discrete
 ) and probability density (continuous
) and probability density (continuous  ) like everyone else. ↵
) like everyone else. ↵  for the Binomial Distribution. ↵
for the Binomial Distribution. ↵- Remember that
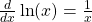 and use the chain rule to notice this. ↵
and use the chain rule to notice this. ↵ - You can probably imagine many ways to continue the Binomial Distribution from
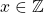 to
to 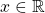 . It doesn't matter which one you pick as long as the behaviour of your new function is not too crazy between the integers; that is,
. It doesn't matter which one you pick as long as the behaviour of your new function is not too crazy between the integers; that is, 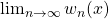 should exist at all
should exist at all 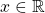 . ↵
. ↵ - Our symbols here are not mathematically clean; we should write something like
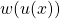 instead of
instead of 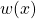 or
or 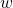 composed with
composed with  at
at  ,
, 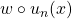 , instead of
, instead of 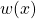 . But to emphasize the intuition we use
. But to emphasize the intuition we use 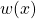 . In clean symbols, the function
. In clean symbols, the function 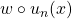 asymptotically approaches
asymptotically approaches  where
where 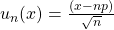 . ↵
. ↵

