17. Overview of the General Linear Model
17.2 The General Linear Model (GLM) for Univariate Statistics
In abstract form, the GLM is
![]()
where
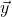 is the data vector, an
is the data vector, an  dimensional column vector.
dimensional column vector.![Rendered by QuickLaTeX.com [X]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-0934d16fbd1e324d448f73ef07c2a631_l3.png) is the design matrix which is different from test type to test type.
is the design matrix which is different from test type to test type.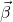 is the parameter vector, a lower
is the parameter vector, a lower 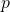 -dimensional vector that summarizes the data in terms of the model given by the design matrix.
-dimensional vector that summarizes the data in terms of the model given by the design matrix.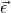 is the error vector, the
is the error vector, the  dimensional column vector of deviations or differences between the model predictions and the data in
dimensional column vector of deviations or differences between the model predictions and the data in 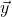 .
.
The solution for ![]() is the least squares solution
is the least squares solution
![]()
In terms of the linear algebra that we just reviewed, ![]() (known as the pseudo-inverse) transforms the data vector
(known as the pseudo-inverse) transforms the data vector ![]() in data space (
in data space (![]() ) to a vector
) to a vector ![]() in parameter space (
in parameter space (![]() ) that presumably explains the data.
) that presumably explains the data.
17.2.1 Linear Regression in GLM Format
We can express the linear regression model ![]() in GLM format as
in GLM format as
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{c} y_{1} \\ y_{2} \\ y_{3} \\ \vdots \\ y_{n} \end{array} \right] = \left[ \begin{array}{cc} 1 & x_{1} \\ 1 & x_{2} \\ 1 & x_{3} \\ \vdots \\ 1 & x_{n} \end{array} \right] \left[ \begin{array}{c} a \\ b \end{array} \right] + \left[ \begin{array}{c} \epsilon_{1} \\ \epsilon_{2} \\ \epsilon_{3} \\ \vdots \\ \epsilon_{n} \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-75ef5b88a108660324220c7d587eb241_l3.png)
Note, importantly, that the design matrix is
![Rendered by QuickLaTeX.com \[[X] = \left[ \begin{array}{cc} 1 & x_{1} \\ 1 & x_{2} \\ 1 & x_{3} \\ \vdots \\ 1 & x_{n} \end{array} \right]\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-d07fe569d46fd7facbe3b1fe9cdc6432_l3.png)
…where the second column is composed of the IV values, ![]() . This is typical for the GLM, the DV is represented by the data vector and the IV is represented by the design matrix. If we do the matrix multiplication the model is:
. This is typical for the GLM, the DV is represented by the data vector and the IV is represented by the design matrix. If we do the matrix multiplication the model is:
![Rendered by QuickLaTeX.com \[\left[ \begin{array}{c} y_{1} \\ y_{2} \\ y_{3} \\ \vdots \\ y_{n} \end{array} \right] = \left[ \begin{array}{c} a + bx_{1} \\ a + bx_{2} \\a + b x_{3} \\ \vdots \\ a + bx_{n} \end{array} \right] + \left[ \begin{array}{c} \epsilon_{1} \\ \epsilon_{2} \\ \epsilon_{3} \\ \vdots \\ \epsilon_{n} \end{array} \right]\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-57842af3dcb38a216bab832c0d01e454_l3.png)
…so ![]() is the prediction vector
is the prediction vector
![Rendered by QuickLaTeX.com \[\vec{\hat{y}} = \left[ \begin{array}{c} \hat{y}_{1} \\ y_{2} \\ \hat{y}_{3} \\ \vdots \\ \hat{y}_{n} \end{array} \right] = \left[ \begin{array}{c} a + bx_{1} \\ a + bx_{2} \\a + b x_{3} \\ \vdots \\ a + bx_{n} \end{array} \right]\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-25b73304857ba7e766d567657ec72c87_l3.png)
Abstractly, the GLM ![]() is
is ![]() and the components of
and the components of ![]() are clearly the deviations
are clearly the deviations ![]() .
.
The least squares solution ![]() written out explicitly for this linear regression case is (without going into the calculation details):
written out explicitly for this linear regression case is (without going into the calculation details):
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[ \begin{array}{c} a \\ b \end{array} \right] &=& \left( \left[ \begin{array}{cccc} 1 & 1 & \cdots & 1 \\ x_{1} & x_{2} & \cdots & x_{n} \end{array} \right] \left[ \begin{array}{cc} 1 & x_{1} \\ 1 & x_{2} \\ \vdots & \vdots \\ 1 & x_{n} \end{array} \right] \right)^{-1} \left[ \begin{array}{cccc} 1 & 1 & \cdots & 1 \\ x_{1} & x_{2} & \cdots & x_{n} \end{array} \right]^{T} \left[ \begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{array} \right] \\ &=& \left[ \begin{array}{c} \frac{(\sum y)(\sum x^{2}) - (\sum x)(\sum x y)}{n(\sum x^{2}) - (\sum x)^{2}} \\ \\ \frac{n(\sum xy) - (\sum x)(\sum y)}{n(\sum x^{2}) - (\sum x)^{2}} \end{array} \right] \end{eqnarray*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-8817975aad537a59b45f75cfc35ed224_l3.png)
…and this is exactly the solution for ![]() and
and ![]() that we saw in Section 14.5: Linear Regression.
that we saw in Section 14.5: Linear Regression.
Example 17.8 : Let’s look at the data of Example 14.3 in a new light. The data were :
| Subject | x | y |
| A | 6 | 82 |
| B | 2 | 86 |
| C | 15 | 43 |
| D | 9 | 74 |
| E | 12 | 58 |
| F | 5 | 90 |
| G | 8 | 78 |
and we found that ![]() (intercept) and
(intercept) and ![]() (slope).
(slope).
In GLM format this all is:
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{c} 82 \\ 86 \\ 43 \\ 74 \\ 58 \\ 90 \\ 78 \end{array} \right] = \left[ \begin{array}{cc} 1 & 6 \\ 1 & 2 \\ 1 & 15 \\ 1 & 9 \\ 1 & 12 \\ 1 & 5 \\ 1 & 8 \end{array} \right] \left[ \begin{array}{c} 102.5 \\ -3.6 \end{array} \right] + \left[ \begin{array}{c} \epsilon_{1} \\ \epsilon_{2} \\ \epsilon_{3} \\ \epsilon_{4} \\ \epsilon_{5} \\ \epsilon_{6} \\ \epsilon_{7} \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-25641bd3c1e2ee3e81dee7e0d3fdeb2b_l3.png)
Exercise: Compute ![]() .
.
▢
17.2.2 Multiple Linear Regression in GLM Format
The model for multiple linear regression with 2 IVs is:
![]()
To see how to cast this model in GLM format, let’s take an ![]() size dataset with data vector
size dataset with data vector
![Rendered by QuickLaTeX.com \[ \vec{y} = \left[ \begin{array}{c} y(1) \\ y(2) \\ y(3) \\ y(4) \\ y(5) \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-c8009880a2a90899c2976a67efed6f5c_l3.png)
…then the GLM ![]() becomes (note the form of
becomes (note the form of ![]() ) :
) :
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{c} y(1) \\ y(2) \\ y(3) \\ y(4) \\ y(5) \end{array} \right] = \left[ \begin{array}{ccc} 1 & x_{1}(1) & x_{2}(1) \\ 1 & x_{1}(2) & x_{2}(2) \\ 1 & x_{1}(3) & x_{2}(3) \\ 1 & x_{1}(4) & x_{2}(4)\\ 1 & x_{1}(5) & x_{2}(5) \end{array} \right] \left[ \begin{array}{c} b_{0} \\ b_{1} \\ b_{2} \end{array} \right] + \left[ \begin{array}{c} \epsilon(1) \\ \epsilon(2) \\ \epsilon(3) \\ \epsilon(4) \\ \epsilon(5) \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-dbef92d00bab705b6469b123e1a942d7_l3.png)
Doing the matrix multiplication and looking at the vector components brings us back to
![]()
![]()
![]()
![]()
![]()
The solution for ![]() again is given by[1]
again is given by[1] ![]() . This is a prescription for deriving the regression formulae but we won’t dive into the details.
. This is a prescription for deriving the regression formulae but we won’t dive into the details.
The design matrix (the model) again maps the ![]() dimensional data vector in
dimensional data vector in ![]() to a parameter vector
to a parameter vector ![]() in
in ![]() . As with all these GLMs, the dimension of the parameter space
. As with all these GLMs, the dimension of the parameter space ![]() is smaller than the dimension
is smaller than the dimension ![]() of the data space. Up until now we have been considering
of the data space. Up until now we have been considering ![]() and
and ![]() as separate vector spaces but we can set things up with[2]
as separate vector spaces but we can set things up with[2] ![]() with the parameter space being a subspace of the data space; in the example here the parameter space is a 3-dimensional subspace of the 5-dimensional data space. That leaves another
with the parameter space being a subspace of the data space; in the example here the parameter space is a 3-dimensional subspace of the 5-dimensional data space. That leaves another ![]() dimensional subspace of the data space that is the noise space. Now we can start to see the signal and noise concepts again. We can also call the parameter space the model space or the signal space so that the
dimensional subspace of the data space that is the noise space. Now we can start to see the signal and noise concepts again. We can also call the parameter space the model space or the signal space so that the ![]() -dimensional data space is composed of a
-dimensional data space is composed of a ![]() -dimensional signal space and a
-dimensional signal space and a ![]() -dimensional noise space. Perfect data would lie in the signal space but in reality the data vector has components in the noise space — it has
-dimensional noise space. Perfect data would lie in the signal space but in reality the data vector has components in the noise space — it has ![]() degrees of freedom for generating random noise. We’ll briefly look at this aspect of data space again in Section 17.2.4.
degrees of freedom for generating random noise. We’ll briefly look at this aspect of data space again in Section 17.2.4.
17.2.3 One-Way ANOVA in GLM Format
There are two ways to formulate a GLM design matrix for one-way ANOVA. It depends on whether the grand mean is explicitly included in the model definition or not. The two model definitions are :
1.) With the grand mean:
![]()
…for group ![]() .
.
2.) Without the grand mean:
![]()
…for group ![]() .
.
We’ll illustrate by means of a simple example that has 3 groups with 2 subjects per group how to construct the ![]() corresponding to each case.
corresponding to each case.
Case 1 : With the grand mean.
![Rendered by QuickLaTeX.com \[ [X] = \left[ \begin{array}{cccc} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-1c7ba849975b562f2e7a5829fb3730d0_l3.png)
The first column of 1’s is for the grand mean and the last three columns are coding vectors for the groups. SPSS uses the GLM setup in its programming. When you enter data for a one-way ANOVA into SPSS, you enter an IV vector that looks like:
![]()
Such a vector is not in GLM form so SPSS takes your IV vector and, behind the scenes[3], produces the 3 coding vectors:
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{c} 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right], \;\; \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \end{array} \right], \;\; \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-d8645bd157125ee5db42ef917af3f4b3_l3.png)
Using the ![]() given above in the GLM, and setting
given above in the GLM, and setting ![]() ,
, ![]() , we get:
, we get:
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{c} y_{1}(1) \\ y_{1}(2) \\ y_{2}(1) \\ y_{2}(2) \\ y_{3}(1) \\ y_{3}(2) \end{array} \right] = \left[ \begin{array}{cccc} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \beta_{0} \\ \beta_{1} \\ \beta_{2} \\ \beta_{3} \end{array} \right] + \left[ \begin{array}{c} \epsilon_{1}(1) \\ \epsilon_{1}(2) \\ \epsilon_{2}(1) \\ \epsilon_{2}(2) \\ \epsilon_{3}(1) \\ \epsilon_{3}(2) \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-8179f36563d166301628c9445b6c322f_l3.png)
…which, with matrix multiplication, expands out to
![]()
![]()
![]()
![]()
![]()
![]()
The solution[4] for ![]() is:
is:
![]()
![]()
…where ![]() is the grand mean of all the data (
is the grand mean of all the data (![]() ) and
) and ![]() is the mean of group
is the mean of group ![]() .
.
Case 2 : Without the grand mean.
![Rendered by QuickLaTeX.com \[ [X] = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-04812f85f40e96a317875aa178cd0669_l3.png)
Now ![]() only contains coding vectors. Using that design matrix in the GLM explicitly for our small example with
only contains coding vectors. Using that design matrix in the GLM explicitly for our small example with ![]() gives:
gives:
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{c} y_{1}(1) \\ y_{1}(2) \\ y_{2}(1) \\ y_{2}(2) \\ y_{3}(1) \\ y_{3}(2) \end{array} \right] = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \beta_{1} \\ \beta_{2} \\ \beta_{3} \end{array} \right] + \left[ \begin{array}{c} \epsilon_{1}(1) \\ \epsilon_{1}(2) \\ \epsilon_{2}(1) \\ \epsilon_{2}(2) \\ \epsilon_{3}(1) \\ \epsilon_{3}(2) \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-9e128d563c8e1b682fe9e75c248d4017_l3.png)
Expanding this to the vector components gives:
![]()
![]()
![]()
![]()
![]()
![]()
Solving ![]() gives:
gives:
![Rendered by QuickLaTeX.com \[\vec{\beta} = \left[ \begin{array}{c} \beta_{1} \\ \beta_{2} \\ \beta_{3} \end{array} \right] = \left[ \begin{array}{c} \overline{x}_{1} \\ \overline{x}_{2} \\ \overline{x}_{3} \end{array} \right]\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-ffd372d3942553418d0904c5e316473d_l3.png)
Let’s work through a numerical example.
Example 17.9 : Given the one-way ANOVA data:
| DV | Group (IV) |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 3 | 2 |
| 2 | 2 |
| 1 | 2 |
| 12 | 3 |
| 11 | 3 |
| 7 | 3 |
| 20 | 4 |
| 21 | 4 |
| 25 | 4 |
…we set up the GLM explicitly without the grand mean :
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{c} 5 \\ 6 \\ 7 \\ 3 \\ 2 \\ 1 \\ 12 \\ 11 \\ 7 \\ 20 \\ 21 \\ 25 \end{array} \right] = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \beta_{1} \\ \beta_{2} \\ \beta_{3} \\ \beta_{4} \end{array} \right] + \left[ \begin{array}{c} \epsilon_{1} \\ \epsilon_{2} \\ \epsilon_{3} \\ \epsilon_{4} \\ \epsilon_{5} \\ \epsilon_{6} \\ \epsilon_{7} \\ \epsilon_{8} \\ \epsilon_{9} \\ \epsilon_{10} \\ \epsilon_{11} \\ \epsilon_{12} \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-2ec8f683865271ad5e86531fdaa1c9b6_l3.png)
The solution for ![]() is
is
![Rendered by QuickLaTeX.com \[\left[ \begin{array}{c} \beta_{1} \\ \beta_{2} \\ \beta_{3} \\ \beta_{4} \end{array} \right] = \left[ \begin{array}{c} \overline{x}_{1} \\ \overline{x}_{2} \\ \overline{x}_{3} \\ \overline{x}_{4} \end{array} \right] = \left[ \begin{array}{c} 6 \\ 2 \\ 10 \\ 22 \end{array} \right]\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-33b8d3c3de9f771db6419f9de9236b5c_l3.png)
…so:
![Rendered by QuickLaTeX.com \[\left[ \begin{array}{c} 5 \\ 6 \\ 7 \\ 3 \\ 2 \\ 1 \\ 12 \\ 11 \\ 7 \\ 20 \\ 21 \\ 25 \end{array} \right] = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} 6 \\ 2 \\ 10 \\ 22 \end{array} \right] + \left[ \begin{array}{c} \epsilon_{1} \\ \epsilon_{2} \\ \epsilon_{3} \\ \epsilon_{4} \\ \epsilon_{5} \\ \epsilon_{6} \\ \epsilon_{7} \\ \epsilon_{8} \\ \epsilon_{9} \\ \epsilon_{10} \\ \epsilon_{11} \\ \epsilon_{12} \end{array} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-1f01c2dde3045cd81950e4d5f03b28a2_l3.png)
Exercise 1 : Do the matrix multiplication and compute ![]() .
.
Exercise 2 : Formulate ![]() with the grand mean and compute
with the grand mean and compute ![]() .
.
Hint: in that case
![Rendered by QuickLaTeX.com \[\vec{\beta} = \left[ \begin{array}{c} \beta_{0} \\\beta_{1} \\ \beta_{2} \\ \beta_{3} \\ \beta_{4} \end{array} \right] = \left[ \begin{array}{c} \overline{x}_{GM} \\ \overline{x}_{1} - \overline{x}_{GM} \\ \ \overline{x}_{2} - \overline{x}_{GM} \\ \overline{x}_{3} - \overline{x}_{GM} \\ \overline{x}_{4} - \overline{x}_{GM} \end{array} \right]\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-41b020f16761c35b3ddce4f3c15ea4c3_l3.png)
…and ![]() will be the same as in Exercise 1.
will be the same as in Exercise 1.
▢
17.2.4 Test Statistics in GLM Format
In all GLM cases the inferential statistics (the ![]() or
or ![]() values) come from an analysis of the
values) come from an analysis of the ![]() error (or residual) vector. Roughly, the approach begins with the observation that
error (or residual) vector. Roughly, the approach begins with the observation that ![]() . The error vector has
. The error vector has ![]() degrees of freedom. Then we consider a variance[5] that has the form
degrees of freedom. Then we consider a variance[5] that has the form
![]()
The ![]() and
and ![]() statistics describe how the component values of
statistics describe how the component values of ![]() will be distributed if
will be distributed if ![]() is true.
is true.
In an ANOVA set up, for example, we can do post hoc testing using contrast vectors[6], ![]() , and use the following formula for the
, and use the following formula for the ![]() test statistic :
test statistic :
![Rendered by QuickLaTeX.com \[ t_{\mbox{test}} = \frac{\vec{c}^{\;T} (\vec{\beta} - \vec{\beta}_{0})}{\sqrt{\sigma^{2} \vec{c}^{\;T}([X]^{T}[X])^{-1} \vec{c}}} \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-99403ecf028fefa43ea212f61959dbba_l3.png)
…where ![]() must be the version without the grand mean and
must be the version without the grand mean and ![]() is the parameter vector associated with
is the parameter vector associated with ![]() (all zeros usually). As examples of contrast vectors, if we have three groups then:
(all zeros usually). As examples of contrast vectors, if we have three groups then:
![Rendered by QuickLaTeX.com \[\vec{c}_{1} & = & \left[ \begin{array}{c} 1 \\ -1 \\ 0 \end{array} \right] \;\;\; \mbox{ compares groups 1 and 2}\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-22379ce9f07fc22ad6df56cc181a4646_l3.png)
![Rendered by QuickLaTeX.com \[\vec{c}_{2} & = & \left[ \begin{array}{c} 1 \\ 0 \\ -1 \end{array} \right] \;\;\; \mbox{ compares groups 1 and 3}\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-a431d407766413c64a478086d799ab86_l3.png)
![Rendered by QuickLaTeX.com \[\vec{c}_{3} & = & \left[ \begin{array}{c} 0 \\ 1 \\ -1 \end{array} \right] \;\;\; \mbox{ compares groups 2 and 3} \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-f97ee31ae822b78b1fcb918e2cc83966_l3.png)
There are similar formulae for ![]() that use the GLM matrices and vectors.
that use the GLM matrices and vectors.
- A more appropriate notation for the parameter vector would be
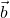 to emphasize that it is an estimate from a sample of some population vector
to emphasize that it is an estimate from a sample of some population vector 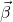 . But, as we did for the symbols
. But, as we did for the symbols  and
and 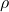 for correlation, we'll be a little sloppy with the notation we use for sample and population values. ↵
for correlation, we'll be a little sloppy with the notation we use for sample and population values. ↵ - The set symbol
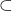 means "proper subset". ↵
means "proper subset". ↵ - The actual operation of SPSS is a blackbox that may not run exactly as described here, but conceptually its GLM operation requires the pieces of
![Rendered by QuickLaTeX.com [X]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-0934d16fbd1e324d448f73ef07c2a631_l3.png) as described here. ↵
as described here. ↵ - You may see that
![Rendered by QuickLaTeX.com [X]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-0934d16fbd1e324d448f73ef07c2a631_l3.png) here is not of full rank so that a least squares solution is not actually possible. But we pick out the solution, from the infinity of possible solutions for
here is not of full rank so that a least squares solution is not actually possible. But we pick out the solution, from the infinity of possible solutions for 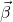 that fits with what we'll find when we look at case 2 in which
that fits with what we'll find when we look at case 2 in which ![Rendered by QuickLaTeX.com [X]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-0934d16fbd1e324d448f73ef07c2a631_l3.png) is of full rank. ↵
is of full rank. ↵ - Again we are being sloppy with sample and population symbols. ↵
- A modern approach, that replaces the traditional omnibus ANOVA followed by post hoc testing, skips the ANOVA and jumps directly to comparing groups of interest using contrast vectors. ↵

