8. Confidence Intervals
8.1 Confidence Intervals Using the z-Distribution
With confidence intervals we will make our first statistical inference. Confidence intervals give us a direct inference about the population from a sample. The probability statement is one about hypotheses about the mean ![]() of the population based on the mean
of the population based on the mean ![]() and standard deviation
and standard deviation ![]() of the sample. This is a fine point. The frequentist definition of probability gives no way to assign a probability to a hypothesis. How do you count hypotheses? The central limit theorem makes a statement about the sample means
of the sample. This is a fine point. The frequentist definition of probability gives no way to assign a probability to a hypothesis. How do you count hypotheses? The central limit theorem makes a statement about the sample means ![]() on the basis of a hypothesis about a population, about its mean
on the basis of a hypothesis about a population, about its mean ![]() and standard deviation
and standard deviation ![]() . If the population is fixed then the central limit theorem gives the results of counting sample means, frequentist probabilities. If we let
. If the population is fixed then the central limit theorem gives the results of counting sample means, frequentist probabilities. If we let ![]() represent a hypothesis about a population (i.e. that it is described by
represent a hypothesis about a population (i.e. that it is described by ![]() and
and ![]() ) and let
) and let ![]() represent data (with mean
represent data (with mean ![]() ) then the central limit theorem gives the probability
) then the central limit theorem gives the probability ![]() . The confidence intervals that we’ll look at first give
. The confidence intervals that we’ll look at first give ![]() . We’ll look at the recipe for computing confidence intervals for means first, then return to this discussion about probabilities for hypotheses.
. We’ll look at the recipe for computing confidence intervals for means first, then return to this discussion about probabilities for hypotheses.
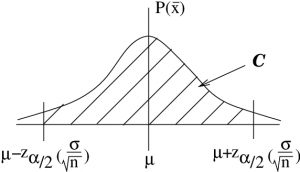
Our goal is to define a symmetric interval about the population mean ![]() that will contain all potentially measured values of
that will contain all potentially measured values of ![]() with a probability[1] of
with a probability[1] of ![]() .
.
Typically ![]() will be
will be
![]()
![]()
![]()
The assumptions that we need in order to use the ![]() -distribution to compute confidence intervals for means are :
-distribution to compute confidence intervals for means are :
- The population standard deviation,
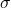 , is known (a somewhat artificial assumption since it is usually not known in an experimental situation) or
, is known (a somewhat artificial assumption since it is usually not known in an experimental situation) or - The sample size is greater than (or equal to) 30,
 and we use
and we use  , the sample standard deviation in our confidence interval formula.
, the sample standard deviation in our confidence interval formula.
Definition : Let ![]() where
where ![]() be the
be the ![]() -value, from the Standard Normal Distribution Table that corresponds to an area, between 0 and
-value, from the Standard Normal Distribution Table that corresponds to an area, between 0 and ![]() of
of ![]() as shown in Figure 8.1.
as shown in Figure 8.1.
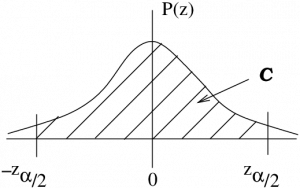
 -distribution areas of interest associated with
-distribution areas of interest associated with  .
.To get our confidence interval we simply inverse ![]() -transform the picture of Figure 8.1, taking the mean of 0 to the sample mean
-transform the picture of Figure 8.1, taking the mean of 0 to the sample mean ![]() and the standard deviation of 1 to the standard error
and the standard deviation of 1 to the standard error ![]() as shown in Figure 8.2.
as shown in Figure 8.2.
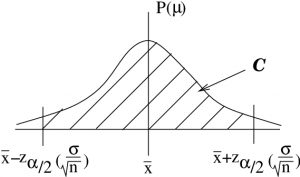
 -transformation of Figure 8.1 gives the confidence interval for
-transformation of Figure 8.1 gives the confidence interval for  .
.So here is our recipe from Figure 8.2. The ![]() -confidence interval for the mean, under one of the two assumptions given above, is :
-confidence interval for the mean, under one of the two assumptions given above, is :
![]()
or using notation that we will use as a standard way of denoting symmetric confidence intervals
(8.1) ![]()
where
![]()
The notation ![]() is more convenient for us than
is more convenient for us than ![]() because we will use the t Distribution Table in the Appendix to find
because we will use the t Distribution Table in the Appendix to find ![]() very quickly. We could equally well write
very quickly. We could equally well write
![]()
but we will use Equation (8.1) because it explicitly gives the bounds for the confidence interval.
Notice how the confidence interval is backwards from the picture that the central limit theorem gives, the picture shown in Figure 8.3. We actually had no business using the inverse ![]() -transformation
-transformation ![]() to arrive at Figure 8.2. It reverses the roles of
to arrive at Figure 8.2. It reverses the roles of ![]() and
and ![]() . We’ll return to this point after we work through the mechanics of an example.
. We’ll return to this point after we work through the mechanics of an example.
Example 8.2 : What is the 95![]() confidence interval for student age if the population
confidence interval for student age if the population ![]() is 2 years, sample
is 2 years, sample ![]() ,
, ![]() ?
?
Solution : So ![]() . First write down the formula prescription so you can see with numbers you need:
. First write down the formula prescription so you can see with numbers you need:
![]()
First determine ![]() . With the tables in the Appendices, there are two ways to do this. The first way is to use the Standard Normal Distribution Table noting that we need the
. With the tables in the Appendices, there are two ways to do this. The first way is to use the Standard Normal Distribution Table noting that we need the ![]() associated with a table area of
associated with a table area of ![]() . Using the table backwards we find
. Using the table backwards we find ![]() . The second way, the recommended way especially during exams, is to use the t Distribution Table. Simply find the column for the 95
. The second way, the recommended way especially during exams, is to use the t Distribution Table. Simply find the column for the 95![]() confidence level and read the
confidence level and read the ![]() from the last line of the table. We quickly find
from the last line of the table. We quickly find ![]() .
.
Either way we now find
![]()
so
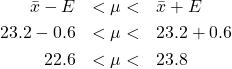
with 95![]() confidence.
confidence.
▢
- Because of this issue about probabilities of hypotheses, many prefer to say "confidence" and not probability. But we will learn enough about Bayesian probability to say "probability". ↵

