3.2 Dispersion: Variance and Standard Deviation

Gordon E. Sarty

3. Descriptive Statistics: Central Tendency and Dispersion

3.2 Dispersion: Variance and Standard Deviation

Variance, and its square root standard deviation, measure how “wide” or “spread out” a data distribution is. We begin by using the formula definitions; they are slightly different for populations and samples.

1. Population Formulae :

Variance :

(3.3) $\begin{equation*} \sigma^2 = \frac{\sum_{i=1}^{N}(x_{i} - \mu)^2}{N}\ \end{equation*}$

where $N$ is the size of the population, $\mu$ is the mean of the population and $x_{i}$ is an individual value from the population.

Standard Deviation :

$\sigma = \sqrt{\sigma^2}$

The standard deviation, $\sigma$ , is a population parameter, we will learn about how to make inferences about population parameters using statistics from samples.

2. Sample Formulae :

Variance :

(3.4) $\begin{equation*} s^{2} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{(n-1)} \end{equation*}$

where $n$ = sample size (number of data points), $n-1$ = degrees of freedom for the given sample, $\overline{x}$ and $x_{i}$ is a data value.

Standard Deviation :

$s = \sqrt{s^2}$

Equations (3.3) and (3.4) are the definitions of variance as the second moment about the mean; you need to determine the means ( $\mu$ or $\overline{x}$ ) before you can compute variance with those formulae. They are algebraically equivalent to a “short cut” formula that allow you to compute the variance directly from sums and sums of squares of the data without computing the mean first. For the sample standard deviation (the useful one) the short cut formula is

(3.5) $\begin{equation*} s^{2} = \frac{\sum_{i=1}^{n}x^{2}_{i} - (\frac{(\sum^n_{i=1}x_i)^2}{n})}{n-1} \end{equation*}$

At this point you should figure out how to compute $\bar{x}$ , $s$ and $\sigma$ on your calculator for a given set of data.

Fact (not proved here) : The sample standard deviation $s$ is the “optimal unbiased estimate” of the population standard deviation $\sigma$ . $s$ is a statistic”, the best statistic it turns out, that is used to estimate the population parameter $\sigma$ . It is the $n-1$ in the denominator that makes $s$ the optimal unbiased estimator of $\sigma$ . We won’t prove that here but we will try and build up a little intuition about what that should be so — why dividing by $n-1$ should be better than dividing by $n$ . ( $n-1$ is known as the degrees of freedom of the estimator $s$ ). First notice that you can’t guess or estimate a value for $\sigma$ (i.e. compute $s$ ) with only one data point. There is no spread of values in a data set of one point! This is part of the reason why the degrees of freedom is $n-1$ and not $n$ . A more direct reason is that you need to remove one piece of information (the mean) from your sample before you can guess $\sigma$ (compute $s$ ).

Coefficient of Variation

The coefficient of variation, CVar, is a “normalized” measure of data spread. It will not be useful for any inferential statistics that we will be doing. It is a pure descriptive statistic. As such it can be useful as a dependent variable but we treat it here as a descriptive statistic that combines the mean and standard deviation. The definition is :

$\mbox{CVar} & = & \frac{s}{\bar{x}} \times 100\% \mbox{\ \ \ \ samples}$

$\mbox{CVar} & = & \frac{\sigma}{\mu} \times 100 \% \mbox{\ \ \ \ population}$

Example 3.9 : In this example we take the data given in the following table as representing the whole population of size $N=6$ . So we use the formula of Equation (3.3) which requires us to sum $(x_{i} - \mu)^2$ .

$x_{i}$

$\left(x_{i}-\mu\right)^{2}$

10

$\left(10-35\right)^{2}$

60

$\left(60-35\right)^{2}$

50

$\left(50-35\right)^{2}$

30

$\left(30-35\right)^{2}$

40

$\left(40-35\right)^{2}$

20

$\left(20-35\right)^{2}$

$\sum x_{i}=210$

$\sum\left(x_{i}-\mu\right)^{2}=1750$

Using the sum in the first column we compute the mean :

$\mu = \frac{\sum x_i}{N} = \frac{210}{6} = 35.$

Then with that mean we compute the quantities in the second (calculation) column above and sum them. And then we may compute the variance :

$\sigma^2 = \frac{\sum(x_i - \mu)^2}{N} = \frac{1750}{6} = 291.7$

and standard deviation

$\sigma = \sqrt{\sigma^2} = \sqrt{291.7} = 17.1.$

Finally, because we can, we compute the coefficient of variation:

$\mbox{CVar} = \frac{\sigma}{\mu} \times 100\% = \frac{17.1}{35} \times 100\% = 48.9\%.$

◻

Example 3.10 : In this example, we have a sample. This is the usual circumstance under which we would compute variance and sample standard deviation. We can use either Equation (3.4) or (3.5). Using Equation (3.4) follows the sample procedure that is given in Example 3.9 and we’ll leave that as an exercise. Below we’ll apply the short-cut formula and see how $s$ may be computed without knowing $\bar{x}$ . The dataset is given in the table below in the column to the left of the double line. The columns to the right of the double line are, as usual, our calculation columns. The size of the sample is $n=6$ .

$x_{i}$

$\left(x_{i}-\overline{x}\right)^{2}$

$x_{i}^{2}$

11.2

$11.2^{2}$ = 125.44

11.9

$11.9^{2}$ = 141.161

12.0

exercise

$12.0^{2}$ = 144

12.8

$12.8^{2}$ = 163.84

13.4

$13.4^{2}$ = 179.56

14.3

$14.3^{2}$ = 204.49

$\sum x_{i}=75.6$

$\sum x_{i}^{2}=958.94$

To find $s$ compute

$s^{2} = \frac{\sum x_{i}^{2} - (\frac{(\sum x_{i})^{2}}{n})}{n-1} = \frac{958.94 - (\frac{5715.36}{6})}{6-1} = \frac{958.94-952.56}{5} = 1.28$

So

$s= \sqrt{s^2} = \sqrt{1.28} = 1.13.$

Note that $s^{2}$ is never negative! If it were then you couldn’t take the square root to find $s$ . Also not that we have not yet determined the mean. We can do that now:

$\bar{x} = \frac{\sum x_i}{n} = \frac{75.6}{6} = 12.60.$

And with the mean we can then compute

$\mbox{CVar }= \frac{s}{\bar{x}} = \frac{1.13}{12.6} \times 100\% = 9.0\%$

◻

Grouped Sample Formula for Variance

As with the mean, we can compute an approximation of the data variance from frequency table, histogram, data. And again this computation is precise for probability distributions with class widths of one. The grouped sample formula for variance is

(3.6) $\begin{equation*} s^{2} = \frac{\sum_{i=1}^{G} (f_{i} \cdot x^{2}_{m_{i}}) - [\frac{(\sum_{i=1}^{G} f_{i} \cdot x_{m_{i}})^2}{n}]}{n-1} \end{equation*}$

where $G$ is the number of groups or classes, $x_{m_{i}}$ is the class center of group $i$ , $f_{i}$ is the frequency of group $i$ and

$n = \sum_{i=1}^{G} f_{i}$

is the sample size. Equation (3.6) the short-cut version of the formula. We can also write

$s^{2} = \frac{\sum_{i=1}^{G} f_{i} (x_{m_{i}} - \mu)^{2}}{n-1}$

or if we are dealing with a population, and the class width is one so that the class center $X_{m_{i}} = X_{i}$ ,

$\sigma^{2} = \frac{\sum_{i=1}^{G} f_{i} (X_{m_{i}} - \mu)^{2}}{N}$

which will be useful when we talk about probability distributions. In fact, let’s look ahead a bit and make the frequentist definition for the probability for $X_{i}$ as $P(X_{i}) = f_{i}/N$ (which is the relative frequency of class $i$ ) so that

(3.7) 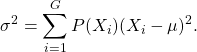$\begin{equation*} \sigma^{2} = \sum_{i=1}^{G} P(X_{i}) (X_{i} - \mu)^{2}. \end{equation*}$

If we make the same substitution $P(X_{i}) = f_{i}/N$ in the grouped mean formula, Equation (3.1) with population items $X$ and $N$ in place of the sample items $x$ and $n$ , then it becomes

(3.8) 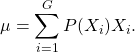$\begin{equation*} \mu = \sum_{i=1}^{G} P(X_{i}) X_{i}. \end{equation*}$

More on probability distributions later, for now let’s see how we use Equation (3.6) for frequency table data.

Example 3.11 : Given the frequency table data to the left of the double dividing line in the table below, compute the variance and standard deviation of the data using the grouped data formula.

Class

Class Boundaries

Freq, $f_{i}$

Class Centre $x_{m_{i}}$

$f_{i}\cdot x_{m_{i}}$

$x^{2}_{m_{i}}$

$f_{i}\cdot x^{2}_{m_{i}}$

1

5.5 – 10.5

1

8

$1\cdot 8 = 8$

$8^{2}=64$

$1\cdot 64 = 64$

2

10.5 – 15.5

2

13

$2\cdot 13 = 26$

$13^{2}=169$

$2\cdot 169 = 338$

3

15.5 – 20.5

3

18

$3\cdot 18 = 54$

$18^{2}=324$

$3\cdot 324 = 972$

4

20.5 – 25.5

5

23

$5\cdot 23 = 115$

$23^{2}=529$

$5\cdot 529 = 2645$

5

25.5 – 30.5

4

28

$4\cdot 28 = 112$

$28^{2}=784$

$4\cdot 784 = 3136$

6

30.5 – 35.5

3

33

$3\cdot 33 = 99$

$33^{2}=1089$

$3\cdot 1089 = 3267$

7

35.5 – 40.5

2

38

$2\cdot 38 = 76$

$38^{2}=1444$

$2\cdot 1444 = 2888$

$\sum f=20$

$\sum fx_{m}=490$

$\sum fx^{2}_{m}=13310$

The formula

$\begin{equation*}s^{2} = \frac{\sum (f x^{2}_{m}) - [\frac{(\sum f x_{m})^2}{n}]}{n-1}\nonumber\end{equation*}$

tells us that we need the sums of $f x^{2}_{m}$ and $f x_{m}$ after we compute the class centres $x_{m}$ and their squares $x^{2}_{m}$ — these calculations we do in the columns added to the right of the double bar in the table above. With the sums we compute

$\begin{equation*} s^{2} &=& \frac{\sum f_{i} x^2_{m_{i}} - [\frac{(\sum f_{i} x_{m_{i}})^2}{n}]}{n-1} \\ &=& \frac{13310 - [\frac{490^{2}}{20}]}{20-1} = \frac{13310-12005}{19} \\ &=& 68.7. \end{equation*}$

So

$\begin{equation*} s = \sqrt{s^{2}} = \sqrt{68.7} = 8.3. \end{equation*}$

The mean, from one of the sums already finished is

$\begin{equation*} \bar{x} = \frac{\sum f_i x_{m_i}}{n} = \frac{490}{20} = 24.5 \end{equation*}$

and the coefficient of variation is

$\begin{equation*} \mbox{CVar} = \frac{s}{\bar{x}} \times 100\% = \frac{8.3}{24.5} \times 100\% = 33.9\% \end{equation*}$

◻

Now is a good time to figure out how to compute $\bar{x}$ and $s$ (and $\sigma$ ) on your calculators.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Share This Book