14. Correlation and Regression
14.6 r² and the Standard Error of the Estimate of y′
Consider the deviations :
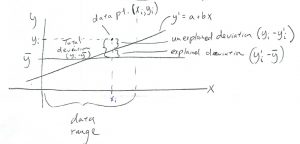
Looking at the picture we see that
![]()
Remember that variance is the sum of the squared deviations (divided by degrees of freedom), so squaring the above and summing gives:
![]()
(the cross terms all cancel because ![]() is the least square solution and
is the least square solution and ![]() , see Section 14.6.1, below, for details). This is also a sum of squares statement:
, see Section 14.6.1, below, for details). This is also a sum of squares statement:
![]()
where SS![]() , SS
, SS![]() and SS
and SS![]() are the sum of squares — error, sum of squares — total and sum of squares — regression (explained) respectively.
are the sum of squares — error, sum of squares — total and sum of squares — regression (explained) respectively.
Dividing by the degrees of freedom, which is ![]() in this {\em bivariate} situation, we get:
in this {\em bivariate} situation, we get:
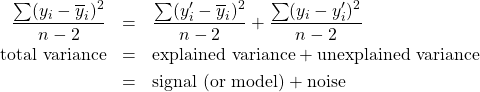
It turns out that
![]()
The quantity ![]() is called the coefficient of determination and gives the the fraction of variance explained by the model (here the model is the equation of a line). The quantity
is called the coefficient of determination and gives the the fraction of variance explained by the model (here the model is the equation of a line). The quantity ![]() appears with many statistical models. For example with ANOVA it turns out that the “effect size” eta-squared is the fraction of variance explained by the ANOVA model[1],
appears with many statistical models. For example with ANOVA it turns out that the “effect size” eta-squared is the fraction of variance explained by the ANOVA model[1], ![]() .
.
The standard error of the estimate is the standard deviation of the noise (the square root of the unexplained variance) and is given by
![]()
Example 14.4: Continuing with the data of Example 14.3, we had
![]()
so

▢
Here is a graphical interpretation of ![]() :
:
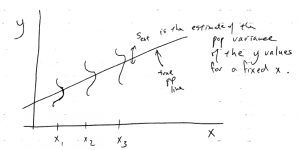
The assumption for computing confidence intervals for is that ![]() is independent of
is independent of ![]() . This is the assumption of homoscedasticity. You can think of the regression situation as a generalized one-way ANOVA where instead of having a finite number of discrete populations for the IV, we have an infinite number of (continuous) populations. All the populations have the same variance
. This is the assumption of homoscedasticity. You can think of the regression situation as a generalized one-way ANOVA where instead of having a finite number of discrete populations for the IV, we have an infinite number of (continuous) populations. All the populations have the same variance ![]() (and they are assumed to be normal) and
(and they are assumed to be normal) and ![]() is the pooled estimate of that variance.
is the pooled estimate of that variance.
14.6.1: **Details: from deviations to variances
Squaring both sides of
![]()
and summing gives
![]()
Working on that cross term, using ![]() , we get
, we get
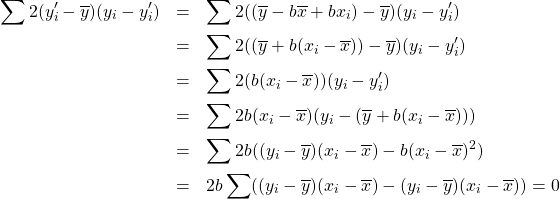
where
![]()
was used in the last line.
- In ANOVA the ``model'' is the difference of means between the groups. We will see more about this aspect of ANOVA in Chapter 17. ↵

