8. Confidence Intervals
8.4 Proportions and Confidence Intervals for Proportions
We will now make use of the approximation of the binomial distribution by the ![]() -distribution given in Section 7.1: Using the Normal Distribution to Approximate the Binomial Distribution. As usual, the confidence interval will switch the roles of population and sample quantities. The recipe will be laid out first, then we will connect it to what you know about the binomial distribution.
-distribution given in Section 7.1: Using the Normal Distribution to Approximate the Binomial Distribution. As usual, the confidence interval will switch the roles of population and sample quantities. The recipe will be laid out first, then we will connect it to what you know about the binomial distribution.
First some definitions. Let ![]() be the number of items in a population of size
be the number of items in a population of size ![]() that have a given quality. (e.g. the number of females in a population; or the number of people at the U of S wearing yellow sweaters). Then the proportion of the population having the given quality is
that have a given quality. (e.g. the number of females in a population; or the number of people at the U of S wearing yellow sweaters). Then the proportion of the population having the given quality is
![]()
Given a sample from the population of size ![]() , the best estimate for
, the best estimate for ![]() is:
is:
![]()
where ![]() is the number of items in the sample having the given quality. To go along with
is the number of items in the sample having the given quality. To go along with ![]() we also have
we also have
![]()
which is is the proportion of items in the sample without the given quality.
To compute an ![]() confidence interval for a proportion
confidence interval for a proportion ![]() we need to compute
we need to compute
![]()
and it must be true that both ![]() and
and ![]() (otherwise we need to use the binomial distribution directly).
(otherwise we need to use the binomial distribution directly).
With ![]() , the
, the ![]() confidence interval for a proportion is given by
confidence interval for a proportion is given by
![]()
To derive the proportions confidence interval formula we’ll begin with the sampling theory given by the binomial distribution and the corresponding ![]() -approximation. Then we’ll switch the roles of
-approximation. Then we’ll switch the roles of ![]() and
and ![]() . Let
. Let
![]()
be the mean, the expected value, of ![]() that you expect to find in a sample of size
that you expect to find in a sample of size ![]() randomly selected from the population with a proportion
randomly selected from the population with a proportion ![]() of items of interest. This is true because
of items of interest. This is true because ![]() is also the probability of randomly selecting an item of interest (the probability of success) from the population as per what we did in Chapter 4. The binomial distribution tells you the probability of getting different numbers
is also the probability of randomly selecting an item of interest (the probability of success) from the population as per what we did in Chapter 4. The binomial distribution tells you the probability of getting different numbers ![]() of items of interest in your sample given
of items of interest in your sample given ![]() . The binomial distribution that describes our situation is shown in Figure 8.7; it has a standard deviation of
. The binomial distribution that describes our situation is shown in Figure 8.7; it has a standard deviation of ![]() .
.
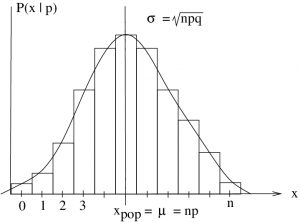
 with
with  items of interest from a population with a proportion
items of interest from a population with a proportion 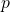 of items of interest. The normal distribution with the same
of items of interest. The normal distribution with the same  and
and 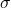 is shown.
is shown.Moving to the normal approximation, we have the picture of Figure 8.8.
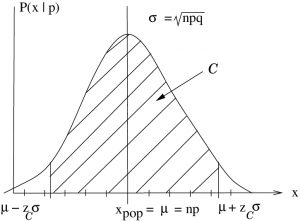
 with
with  items of interest from a population with a proportion
items of interest from a population with a proportion 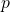 of items of interest. The boundaries of the area
of items of interest. The boundaries of the area 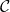 follow from an inverse
follow from an inverse  -transform of the
-transform of the  -distribution to a normal distribution of mean
-distribution to a normal distribution of mean  and standard deviation
and standard deviation 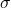 ,
, 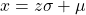 .
.Figure 8.8 says :
![]()
with a (frequentist) probability of ![]() . This is our sampling theory. Divide by
. This is our sampling theory. Divide by ![]() :
:
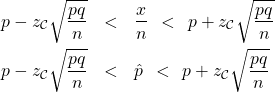
Swapping the roles of the population and sample, we arrive at the confidence interval formula :
![]()
Time for a worked example.
Example 8.3 : A sample of 500 nursing applications included 60 men. Find the 90% confidence interval of the true proportion of men who applied to the nursing program.
Solution : From the t Distribution Table, look up
![]()
and compute
![]()
![]()
![]()
Then
![]()
![]()
![]()
is the confidence interval with 90% confidence.
▢
Sample size need for a poll
Measuring proportions is what pollsters do. For example in an election you might want to know how many people will vote for liberals (items of interest) and how many will vote for conservatives (items not of interest)[1] In a news paper you might see: “The poll says that 72![]() of the voters will vote liberal. The poll is considered accurate to 2 percentage points 19 time out of 20.” This means that the 95
of the voters will vote liberal. The poll is considered accurate to 2 percentage points 19 time out of 20.” This means that the 95![]() confidence interval (19/20 = 0.95) of the proportion of liberal voters is
confidence interval (19/20 = 0.95) of the proportion of liberal voters is ![]() (note how proportions are presented as percentages in the newspaper). The error here is
(note how proportions are presented as percentages in the newspaper). The error here is ![]() . Before the pollster starts telephoning people, she must know how many people to phone to arrive at that goal error of 2
. Before the pollster starts telephoning people, she must know how many people to phone to arrive at that goal error of 2![]() . She needs to know what the sample size
. She needs to know what the sample size ![]() needed is. In general, the minimum sample size needed to attain a goal error
needed is. In general, the minimum sample size needed to attain a goal error ![]() on a confidence interval of
on a confidence interval of ![]() is
is
![]()
Here ![]() and
and ![]() could come from a previous survey if available. If there is no such survey or if you want to be sure of ending up with an error equal to or less than a goal E, then use
could come from a previous survey if available. If there is no such survey or if you want to be sure of ending up with an error equal to or less than a goal E, then use ![]() , see Figure 8.9.
, see Figure 8.9.
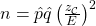 is a quadratic formula. Substitute
is a quadratic formula. Substitute 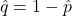 to get
to get 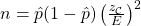 or
or 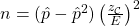 . The maximum of
. The maximum of 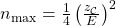 is at
is at 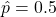 .
.Example 8.4 : We want to estimate, with 95![]() confidence, the proportion of people who own a home computer. A previous study gave an answer of 40
confidence, the proportion of people who own a home computer. A previous study gave an answer of 40![]() . For a new study we want an error of 2
. For a new study we want an error of 2![]() . How many people should we poll?
. How many people should we poll?
Solution : From the question we have :
![]()
![]()
From the t Distribution Table (or the Standard Normal Distribution Table if you think about the areas correctly) we find
![]()
Therefore
![]()
Which we round up to a sample size of 2305 to ensure that ![]() .
.
▢
- We assume here that there are only two parties. For the real life situation of more than two parties we need the multinomial distribution and to approximate it with a multivariate normal distribution. That is a topic for multivariate statistics but the principles are the same as what we cover here. ↵

