8.2 **Bayesian Statistics

Now that we’ve seen how easy it is to compute confidence intervals, let’s give it a proper probabilistic meaning. To extend probability from the frequentist definition to the Bayesian definition, we need Bayes’ rule. Bayes’ rule is, for events and :

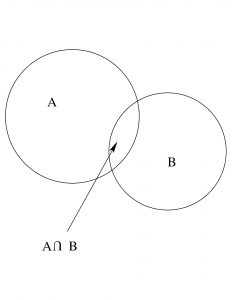
Study Figure 8.4 to convince yourself that Bayes’ rule is true. Notice that

and

So, equating from each of those two perspectives, we get Bayes’ rule.

If we let (hypothesis) and (data), Bayes’ rule gives us a way to define the probability of hypothesis through

(8.2)  

The quantity is known as the prior probability of the data relative to the hypothesis and is something that can be computed in theory if probabilities are assigned in a reasonable manner. The specification of prior probabilities is a contentious issue with the Bayesian approach. Really, it represents a prior belief. The quantity is what sampling theory, like the central limit theorem, gives and is known as the likelihood. Finally the quantity is known as the posterior probability. Equation (8.2) is an expression about probability distributions as well as individual probabilities (just allow and to vary).

If we assign for the prior probability then . We can switch the roles of and ! Of course is not a probability distribution because the area under a function whose value is always 1 is infinite. The area under a probability distribution must be 1. So is an improper distribution (as a function of either or ). But note that an improper distribution times a proper distribution here gives rise to a proper distribution. With this slight of hand, we can give confidence intervals a probabilistic interpretation.