16. Non-parametric Tests
16.8 SPSS Lesson 14: Non-parametric Tests
16.8.1 Mann Whitney/Wilcoxson Rank Sum
The Mann Whitney/Wilcoxson Rank Sum tests is a non-parametric alternative to the independent sample ![]() -test. So the data file will be organized the same way in SPSS: one independent variable with two qualitative levels and one independent variable. Open “RetinalAnatomyData.sav” from the textbook Data Sets :
-test. So the data file will be organized the same way in SPSS: one independent variable with two qualitative levels and one independent variable. Open “RetinalAnatomyData.sav” from the textbook Data Sets :
Choose Analyze ![]() Nonparametric Tests
Nonparametric Tests ![]() Legacy Dialogues
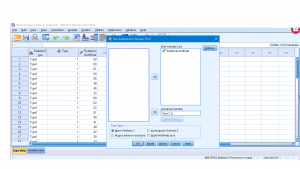
Legacy Dialogues ![]() 2 Independent Samples. Then set-up :
2 Independent Samples. Then set-up :
Running the test produces :
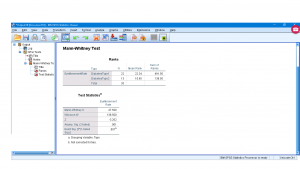
The first table has sums of the ranks including the sum of ranks of the smaller sample, ![]() , and the sample sizes
, and the sample sizes ![]() and
and ![]() that you could use to manually compute
that you could use to manually compute ![]() if you wanted to. The test statistic
if you wanted to. The test statistic ![]() shows up in the second table along with
shows up in the second table along with ![]() which means that you can marginally reject
which means that you can marginally reject ![]() for a two-tail test. When we did this test by hand, we required
for a two-tail test. When we did this test by hand, we required ![]() ,
, ![]() so that the
so that the ![]() test statistic would be valid. In the SPSS output two other test statistics,
test statistic would be valid. In the SPSS output two other test statistics, ![]() and
and ![]() that can be used for smaller sample sizes. The exact
that can be used for smaller sample sizes. The exact ![]() -value is given in the last line of the output; the asymptotic
-value is given in the last line of the output; the asymptotic ![]() -value is the one associated with
-value is the one associated with ![]() . When the asymptotic
. When the asymptotic ![]() -value equals the exact one, then the
-value equals the exact one, then the ![]() test statistic is a good approximation — this should happen when
test statistic is a good approximation — this should happen when ![]() ,
, ![]() .
.
16.8.2 Paired Wilcoxon Signed Rank Test and Paired Sign Test
Open “MigraineTriggeringData.sav” from the textbook Data Sets :
We will see if there is a significant difference between pay and security (![]()
![]() ). Pull up Analyze
). Pull up Analyze ![]() Nonparametric Tests
Nonparametric Tests ![]() Legacy Dialogues
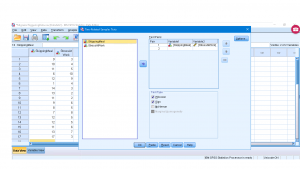
Legacy Dialogues ![]() 2 Related Samples to get :
2 Related Samples to get :
The output for the paired Wilcoxon signed rank test is :
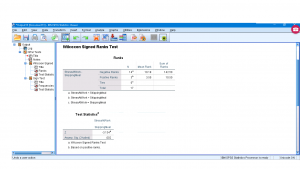
From the output we see that ![]() . The test statistic
. The test statistic ![]() with
with ![]() so the mean difference is significantly different from zero.
so the mean difference is significantly different from zero.
The output for the paired sign test (![]() MD difference
MD difference ![]() ) is :
) is :
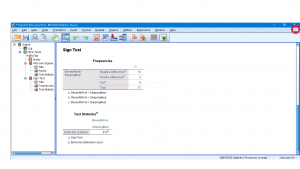
Here we see (remembering the definitions) that ![]() . Since
. Since ![]() we can conclude that “Skipping Meal” is significantly different from “Stress at Work” (more negative differences and the difference is significant).
we can conclude that “Skipping Meal” is significantly different from “Stress at Work” (more negative differences and the difference is significant).
16.8.3 Kruskal-Wallis Test
Open “CancerTumourReduction.sav” from the textbook Data Sets :
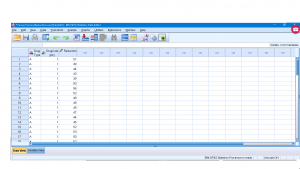
The independent variable, group, has three levels; the dependent variable is diff. Choose Analyze ![]() Nonparametric Tests
Nonparametric Tests ![]() Legacy Dialogues
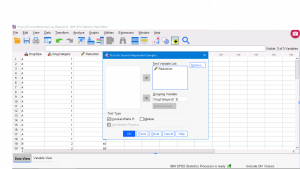
Legacy Dialogues ![]() K Independent Samples and set up the dialogue menu this way, with 1 and 3 being the minimum and maximum values defined in the Define Range menu:
K Independent Samples and set up the dialogue menu this way, with 1 and 3 being the minimum and maximum values defined in the Define Range menu:
Running the test gives:
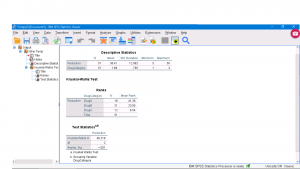
There is enough information to compute the test statistic ![]() which is labeled as Chi-Square in the SPSS output. That is
which is labeled as Chi-Square in the SPSS output. That is ![]() and it is significant (
and it is significant (![]() ) so at least one of the group means is significantly different from the others. Also we see
) so at least one of the group means is significantly different from the others. Also we see ![]() . Notice that the sums of the ranks are not given directly but sum of ranks = Mean Rank
. Notice that the sums of the ranks are not given directly but sum of ranks = Mean Rank ![]() N.
N.

