10. Comparing Two Population Means
10.4 Unpaired or Independent Sample t-Test
In comparing the variances of two populations we have one of two situations :
- Homoscedasticity :
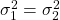
- Heteroscedasticity :
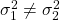
These terms also apply when there are more than 2 populations. They either all have the same variance, or not. This affects how we do an independent sample ![]() -test because we have two cases :
-test because we have two cases :
1. Variances of the two populations assumed unequal. ![]() .
.
Then the test statistic is :
![Rendered by QuickLaTeX.com \[t_{\rm test} = \frac{(\bar{x}_1 - \bar{x}_2)}{\sqrt{\frac{s^2_1}{n_1} + \frac{s^2_1}{n_2}}}\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-17a3beb6bedbea8e6bd3732a4496bbfc_l3.png)
This is the same formula as we used for the ![]() -test. To find the critical statistic we will use, when solving problems by hand, degrees of freedom
-test. To find the critical statistic we will use, when solving problems by hand, degrees of freedom
(10.2) ![]()
This choice is a conservative approach (harder to reject ![]() ). SPSS uses a more accurate
). SPSS uses a more accurate
(10.3) ![Rendered by QuickLaTeX.com \begin{equation*} \nu = \frac{\left( \frac{s^2_1}{n_1} + \frac{s_2^2}{n_2} \right)^2}{\left[ \frac{\left( \frac{s^2_1}{n_1} \right)}{n_1-1} + \frac{\left( \frac{s^2_2}{n_2} \right)}{n_{2}-1} \right]} \end{equation*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-bb03778ab34703291fdcfc22e87448fe_l3.png)
You will not need to use Equation (10.3), only Equation (10.2). Equation (10.3) gives fractional degrees of freedom. The ![]() test statistic for this case and the degrees of freedom in Equation (10.3) is know as the Satterwaite approximation. The
test statistic for this case and the degrees of freedom in Equation (10.3) is know as the Satterwaite approximation. The ![]() -distributions are strictly only applicable if
-distributions are strictly only applicable if ![]() . The Satterwaite approximation is an adjustment to make the
. The Satterwaite approximation is an adjustment to make the ![]() -distributions fit this
-distributions fit this ![]() case.
case.
2. Variances of the two populations assumed equal. ![]() .
.
In this case the test statistic is:
![Rendered by QuickLaTeX.com \[t_{\rm test} = \frac{(\bar{x}_1 - \bar{x}_2)}{\sqrt{\frac{(n_1-1)s^2_1 + (n_2-1)s^2_2}{n_1 + n_2 - 2}} \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-4013d564cf1bd48e8ac0a1957c6e9f15_l3.png)
This test statistic formula can be made more intuitive by defining
(10.4) 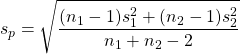
as the pooled estimate of the variance. ![]() is the data estimate for the common population
is the data estimate for the common population ![]() .
. ![]() is the weighted mean of the sample variances
is the weighted mean of the sample variances ![]() and
and ![]() . Recall the generic weighted mean formula, Equation (3.2). The weights are
. Recall the generic weighted mean formula, Equation (3.2). The weights are ![]() and
and ![]() ; their sum is
; their sum is ![]() . In other words
. In other words
![]()
and we can write the test statistic as
(10.5) 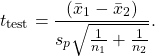
See that ![]() is clearly a standard error of the mean.
is clearly a standard error of the mean.
10.4.1 General form of the t test statistic
All ![]() statistics have the form :
statistics have the form :
![]()
Remember that! Memorizing complicated formulae is useless, but you should remember the basic form of a ![]() test statistic.
test statistic.
10.4.2 Two step procedure for the independent samples t test
Example 10.4: Case 1 example.
Given the following data summary :
(Note that ![]() . If that wasn’t true, we could reverse the definitions of populations 1 and 2 so that
. If that wasn’t true, we could reverse the definitions of populations 1 and 2 so that ![]() .) Is
.) Is ![]() significantly different from
significantly different from ![]() ? That is, is
? That is, is ![]() different from
different from ![]() ? Test at
? Test at ![]() .
.
Solution :
So the question is to decide between
![]()
a two-tailed test. But before we can test the question, we have to decide which ![]() test statistic to use: case 1 or 2. So we need to do two hypotheses tests in a row. The first one to decide which
test statistic to use: case 1 or 2. So we need to do two hypotheses tests in a row. The first one to decide which ![]() statistic to use, the second one to test the hypotheses of interest given above.
statistic to use, the second one to test the hypotheses of interest given above.
Test 1 : See if variances can be assumed equal or not.
1. Hypothesis.
![]()
(Always use a two-tailed hypothesis when using the ![]() test to decide between case 1 and 2 for the
test to decide between case 1 and 2 for the ![]() test statistic.)
test statistic.)
2. Critical statistic.
![]()
(from the F Distribution Table)
(Here we used ![]() given for the
given for the ![]() -test question. But that is not necessary. You can use
-test question. But that is not necessary. You can use ![]() in general; the consequence of a type I error here is small because the
in general; the consequence of a type I error here is small because the ![]() -test is robust to violations of the assumption of homoscedasticity.)
-test is robust to violations of the assumption of homoscedasticity.)
3. Test statistic.
![]()
4. Decision.
![]() (
(![]() — drawing a picture would be a safe thing to do here as usual) so reject
— drawing a picture would be a safe thing to do here as usual) so reject ![]() .
.
5. Interpretation.
Assume the variances are unequal, ![]() , and use the
, and use the ![]() test statistic of case 1.
test statistic of case 1.
Test 2 : The question of interest.
1. Hypothesis.
![]()
2. Critical statistic.
From the t Distribution Table, with ![]() , and a two-tailed test with
, and a two-tailed test with ![]() we find
we find
![]()
3. Test Statistic.
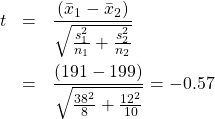
The ![]() -value may be estimated from the t Distribution Table using the procedure given in Chapter 9: from the t Distribution Table,
-value may be estimated from the t Distribution Table using the procedure given in Chapter 9: from the t Distribution Table, ![]() line, find the values that bracket 0.57. There are none, the smallest value is 0.711 corresponding to
line, find the values that bracket 0.57. There are none, the smallest value is 0.711 corresponding to ![]() . So all we can say is
. So all we can say is ![]() .
.
4. Decision.
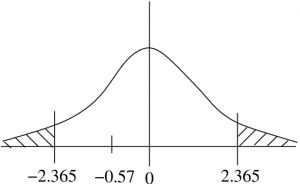
![]() is not in the rejection region so do not reject
is not in the rejection region so do not reject ![]() . The estimate for the
. The estimate for the ![]() -value confirms this decision.
-value confirms this decision.
5. Interpretation.
There is not enough evidence, at ![]() with the independent sample
with the independent sample ![]() -test, to conclude that the means of the populations are different.
-test, to conclude that the means of the populations are different.
▢
Example 10.5 (Case 2 example) :
The following data seem to show that private nurses earn more than government nurses :
| Private Nurses Salary | Government Nurses Salary |
Testing at ![]() , do private nurses earn more than government nurses?
, do private nurses earn more than government nurses?
Solution :
First confirm, or change, the population definitions so that ![]() . This is already true so we are good to go.
. This is already true so we are good to go.
Test 1 : See if variances can be assumed equal or not. This is a test of ![]() vs.
vs. ![]() . After the test we find that we believe that
. After the test we find that we believe that ![]() at
at ![]() . So we will use the case 2, equal variances,
. So we will use the case 2, equal variances, ![]() -test formula for test 2, the test of interest.
-test formula for test 2, the test of interest.
Test 2 : The question of interest.
1. Hypothesis.
![]()
![]()
(Note how ![]() reflects the face value of the data, that private nurses appear to earn more than government nurses in the population — it is true in the samples.)
reflects the face value of the data, that private nurses appear to earn more than government nurses in the population — it is true in the samples.)
2. Critical statistic.
Use the t Distribution Table, one-tailed test, ![]() (column) and
(column) and ![]() to find
to find
![]()
3. Test statistic.

To estimate the ![]() -value, look at the
-value, look at the ![]() line in the t Distribution Table to see if there are a pair of numbers that bracket
line in the t Distribution Table to see if there are a pair of numbers that bracket ![]() . They are all smaller than 5.47 so
. They are all smaller than 5.47 so ![]() is less than the
is less than the ![]() associated with the largest number 2.921 whose
associated with the largest number 2.921 whose ![]() is 0.005 (one-tailed, remember). So
is 0.005 (one-tailed, remember). So ![]() .
.
4. Decision.
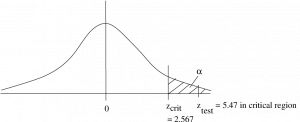
Reject ![]() since
since ![]() is in the rejection region and
is in the rejection region and ![]() .
.
![]()
5. Interpretation.
From a ![]() -test at
-test at ![]() , there is enough evidence to conclude that private nurses earn more than government nurses.
, there is enough evidence to conclude that private nurses earn more than government nurses.
▢

