12. ANOVA
12.8 Higher Factorial ANOVA
We’ve seen 1-way ANOVA and 2-way ANOVA but it doesn’t have to stop there. We can have any number of factors, or independent variables. We can have 3-way ANOVA, 4-way ANOVA, etc. In general we can have an ![]() -way ANOVA. An
-way ANOVA. An ![]() -way ANOVA will have
-way ANOVA will have ![]() IVs (
IVs (![]() factors) but still only one DV.
factors) but still only one DV.
12.8.1 3-way ANOVA
A 3-way ANOVA will have 3 factors (IVs): ![]() ,
, ![]() , and
, and ![]() with
with ![]() ,
, ![]() and
and ![]() levels respectively. A 3-way ANOVA will test 7 hypotheses (all of which are one-way ANOVAs) :
levels respectively. A 3-way ANOVA will test 7 hypotheses (all of which are one-way ANOVAs) :
- Main effect of
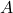 (collapse across
(collapse across 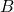 and
and 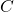 ).
). - Main effect of
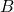 (collapse across
(collapse across 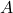 and
and 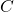 ).
). - Main effect of
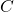 (collapse across
(collapse across 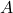 and
and 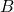 ).
). - 2-way interaction
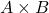 (collapse across
(collapse across 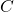 ).
). - 2-way interaction
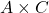 (collapse across
(collapse across 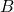 ).
). - 2-way interaction
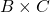 (collapse across
(collapse across 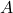 ).
). - 3-way interaction
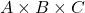 .
.
So there will be 7 test statistics to consider:
![]()
The profile plots for a 3-way ANOVA are intrinsically 4-dimensional and so can be difficult to draw. One approach is to make ![]() 2-way style ANOVA plots :
2-way style ANOVA plots :

The interpretation of a 3-way interaction can be tough and there will be many post-hoc pairwise comparisons of cells that may be meaningful. For these reasons it is best to be more reductionist in your experiment designs so that you never have to use a 3-way ANOVA. A design that uses preplanned contrasts is usually better than one that requires a 3 (or higher) way ANOVA.
For an ![]() -way ANOVA, there will be
-way ANOVA, there will be
![]()
hypotheses to test, each with an associated ![]() test statistic. The number of profile plots to consider will be large and will necessarily involve collapsing factors because the data exist in an
test statistic. The number of profile plots to consider will be large and will necessarily involve collapsing factors because the data exist in an ![]() dimensional space (number of IVs plus DV). Interpretation will be a nightmare. An
dimensional space (number of IVs plus DV). Interpretation will be a nightmare. An ![]() -dimensional ANOVA for
-dimensional ANOVA for ![]() is more of a mathematical curiosity than a useful scientific tool.
is more of a mathematical curiosity than a useful scientific tool.

