9. Hypothesis Testing
9.3 t-Test for Means
Hypothesis testing for means for sample set sizes in ![]() where
where ![]() is used as an estimate for
is used as an estimate for ![]() is the same as for
is the same as for ![]() except that
except that ![]() and not
and not ![]() is the test statistic[1]. Specifically, the test statistic is
is the test statistic[1]. Specifically, the test statistic is
![]()
for ![]() from any of the hypotheses listed in the table you saw in the previous section (one- and two-tailed versions):
from any of the hypotheses listed in the table you saw in the previous section (one- and two-tailed versions):
| Two-Tailed Test | Right-Tailed Test | Left-Tailed Test |
The critical statistic is found in the t Distribution Table with the degrees of freedom ![]() .
.
Example 9.4 : A physician claims that joggers, maximal volume oxygen uptake is greater than the average of all adults. A sample of 15 joggers has a mean of 40.6 ml/kg and a standard deviation of 6 ml/kg. If the average of all adults is 36.7 ml/kg, is there enough evidence to support the claim at ![]() ?
?
1. Hypothesis.
![]()
![]() (claim)
(claim)
2. Critical statistic.
In the t Distribution Table, find the column for one-tailed test at ![]() and the line for degrees of freedom
and the line for degrees of freedom ![]() . With that find
. With that find
![]()
3. Test statistic.
![]()
To compute this we need : ![]() ,
, ![]() and
and ![]() from the problem statement. From the hypothesis we have
from the problem statement. From the hypothesis we have ![]() . So
. So
![]()
At this point we can estimate the ![]() -value using the t Distribution Table, which doesn’t have as much information about the
-value using the t Distribution Table, which doesn’t have as much information about the ![]() -distribution as the Standard Normal Distribution Table has about the
-distribution as the Standard Normal Distribution Table has about the ![]() -distribution, so we can only estimate. The procedure is: In the
-distribution, so we can only estimate. The procedure is: In the ![]() row, look for
row, look for ![]() values that bracket
values that bracket ![]() . They are 2.145 (with
. They are 2.145 (with ![]() in the column heading for one-tailed tests) and 2.624 (associated with a one-tail
in the column heading for one-tailed tests) and 2.624 (associated with a one-tail ![]() ).
).
So,
![]()
is our estimate[2] for ![]() .
.
4. Decision.
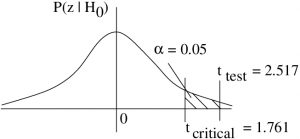
Reject ![]() . We can also base this decision on our
. We can also base this decision on our ![]() -value estimate since :
-value estimate since :
![]()
5. Interpretation.
There is enough evidence to support the claim that the joggers’ maximal volume oxygen uptake is greater than 36.7 ml/kg using a ![]() -test at
-test at ![]() .
.
▢
Fine point. When we use ![]() in a
in a ![]() (or
(or ![]() test) as an estimate for
test) as an estimate for ![]() , we are actually assuming that distribution of sample means is normal. The central limit theorem tells us that the distribution of sample means is approximately normal so generally we don’t worry about this restriction. If the population is normal then the distribution of sample means will be exactly normal. Some stats texts state that we need to assume that the population is normal for a
, we are actually assuming that distribution of sample means is normal. The central limit theorem tells us that the distribution of sample means is approximately normal so generally we don’t worry about this restriction. If the population is normal then the distribution of sample means will be exactly normal. Some stats texts state that we need to assume that the population is normal for a ![]() -test to be valid. However, the central limit theorem’s conclusion guarantees that the
-test to be valid. However, the central limit theorem’s conclusion guarantees that the ![]() -test is robust to violations of that assumption. If the population has a very wild distribution then
-test is robust to violations of that assumption. If the population has a very wild distribution then ![]() may be bad estimate for
may be bad estimate for ![]() because the distribution of sample
because the distribution of sample ![]() values will not follow the
values will not follow the ![]() distribution. The chance if this happening becomes smaller the larger the
distribution. The chance if this happening becomes smaller the larger the ![]() , again by the central limit theorem.
, again by the central limit theorem.
Origin of the ![]() -distribution
-distribution
We can easily define the ![]() -distribution via random variables associated with the following stochastic processes. Let :
-distribution via random variables associated with the following stochastic processes. Let :
![]()
Then the random variable
![]()
is a random variable that follows a ![]() -distribution with
-distribution with ![]() degrees of freedom.
degrees of freedom.

