13. Power
13.1 Power
Power is a concept that applies to all statistical testing. Here we will look at power quantitatively for the ![]() -test for means (
-test for means (![]() -test with large
-test with large ![]() ). We will see explicitly in that case some principles that apply to other tests. These principles are: the bigger your sample size (
). We will see explicitly in that case some principles that apply to other tests. These principles are: the bigger your sample size (![]() ), the higher the power; the larger
), the higher the power; the larger ![]() is, the more power there is[1]; the larger the “effect size” is the more power there is. A final principle, that we can’t show by restricting ourselves to a
is, the more power there is[1]; the larger the “effect size” is the more power there is. A final principle, that we can’t show by restricting ourselves to a ![]() -test, is that the simpler the statistical test, the more power it has — being clever doesn’t get you anywhere in statistics.
-test, is that the simpler the statistical test, the more power it has — being clever doesn’t get you anywhere in statistics.
Let’s being by recalling the “confusion matrix” (here labelled a little differently than the one shown in Chapter 9 to emphasize the decision making). Note: The ![]() ,
, ![]() , etc. quantities are the probabilities that each conclusion will happen.
, etc. quantities are the probabilities that each conclusion will happen.
| Reality | |||
| Conclusion of Test | Type I error |
Correct decision |
|
| Correct decision |
Type II error |
||
Recall that ![]() is the power, the probability of correctly rejecting
is the power, the probability of correctly rejecting ![]() . With the definition of
. With the definition of ![]() as not
as not ![]() , we cannot actually compute a power because this definition is too vague. The confusion matrix with
, we cannot actually compute a power because this definition is too vague. The confusion matrix with ![]() and
and ![]() as given here is purely a conceptual device. To actually compute a power number we need to nail down a specific alternate hypothesis
as given here is purely a conceptual device. To actually compute a power number we need to nail down a specific alternate hypothesis ![]() and compute
and compute ![]() for the more specific confusion matrix:
for the more specific confusion matrix:
| Reality | |||
| Conclusion of Test | Type I error |
Correct decision (power) |
|
| Correct decision |
Type II error |
||
We will define ![]() and
and ![]() be three parameters. The first is that we assume that the populations associated with
be three parameters. The first is that we assume that the populations associated with ![]() and
and ![]() both have the same standard deviation
both have the same standard deviation ![]() . Then, assuming that both populations are normal,
. Then, assuming that both populations are normal, ![]() is defined by its population mean
is defined by its population mean ![]() (we used
(we used ![]() in Chapter 9) and
in Chapter 9) and ![]() is defined by its population mean
is defined by its population mean ![]() .
.
We can define two flavors of power :
- Predicted power. Based on a pre-defined alternate mean
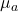 of interest and an estimate of
of interest and an estimate of 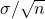 . The population standard deviation
. The population standard deviation 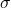 is frequently estimated from the sample standard deviation
is frequently estimated from the sample standard deviation  of a small pilot study.
of a small pilot study. - Observed power. Based on the observed sample mean
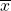 which is then used as the alternate mean
which is then used as the alternate mean 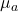 and sample standard deviation
and sample standard deviation  which is used for
which is used for 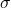 .
.
The type II error rate ![]() (and power
(and power ![]() ) is calculated by considering the populations associated with
) is calculated by considering the populations associated with ![]() and
and ![]() :
:
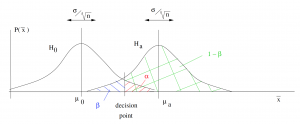
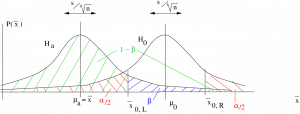
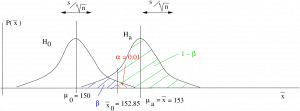
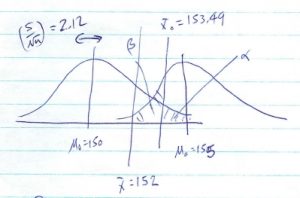
This picture follows directly from the Central Limit Theorem. Hypothesis testing is a decision process. In the picture above, which shows a one-tailed ![]() -test for means, you reject
-test for means, you reject ![]() if
if ![]() falls to the right of the decision point. The decision point is set by the value of
falls to the right of the decision point. The decision point is set by the value of ![]() . Note that the alternate mean
. Note that the alternate mean ![]() needs to be in the rejection region of
needs to be in the rejection region of ![]() for the picture to make sense. The value of
for the picture to make sense. The value of ![]() (and hence the power
(and hence the power ![]() ) depends on the magnitude of the effect size[2]
) depends on the magnitude of the effect size[2] ![]() . We can see that power will increase if the effect size that we are looking for in our experiment increases. This makes sense because larger differences should be easier to measure. Also note that if
. We can see that power will increase if the effect size that we are looking for in our experiment increases. This makes sense because larger differences should be easier to measure. Also note that if ![]() increases, as it would by replicating an experiment with a larger sample size, then the two distributions of sample means will get skinner and, for a given effect size, the power will increase. Again, this makes intuitive sense because more data is always better. We will illustrate these features in the numerical examples that follow.
increases, as it would by replicating an experiment with a larger sample size, then the two distributions of sample means will get skinner and, for a given effect size, the power will increase. Again, this makes intuitive sense because more data is always better. We will illustrate these features in the numerical examples that follow.
For the purpose of learning the mechanics of statistical power we focus on observed power. With observed power we use the sample data for the power calculations; set ![]() and
and ![]() . Since
. Since ![]() needs to be in the rejection region of
needs to be in the rejection region of ![]() , observed power can only be computed when the conclusion of the hypothesis test is to reject
, observed power can only be computed when the conclusion of the hypothesis test is to reject ![]() . In real life if you reject
. In real life if you reject ![]() you don’t care about what power the experiment had to reject
you don’t care about what power the experiment had to reject ![]() . It’s a bit like calculating if you have enough gas to drive to Regina after you’ve arrived at Regina. In real life you will care about power only if you fail to reject
. It’s a bit like calculating if you have enough gas to drive to Regina after you’ve arrived at Regina. In real life you will care about power only if you fail to reject ![]() because you will want to know the problem was that you tried to measure too small of an effect size or if a larger sample might lead to a decision to reject
because you will want to know the problem was that you tried to measure too small of an effect size or if a larger sample might lead to a decision to reject ![]() . In that case you will need to decide what effect size, or sample size, to use in computing a predicted power. You will use predicted power in your experiment design. If your experiment design has a predicted power of about 0.80 then you have a reasonable chance of rejecting the null hypothesis. If your research involves invasive intervention with people (needles, surgery, etc.) then you may need to present a power calculation to prove to an ethics committee that your experiment has a reasonable chance of finding what you think it will find.
. In that case you will need to decide what effect size, or sample size, to use in computing a predicted power. You will use predicted power in your experiment design. If your experiment design has a predicted power of about 0.80 then you have a reasonable chance of rejecting the null hypothesis. If your research involves invasive intervention with people (needles, surgery, etc.) then you may need to present a power calculation to prove to an ethics committee that your experiment has a reasonable chance of finding what you think it will find.
In addition to ![]() and
and ![]() we need the value of the decision point
we need the value of the decision point ![]() which is the inverse
which is the inverse ![]() -transform of
-transform of ![]() . We’ll consider three cases :
. We’ll consider three cases :
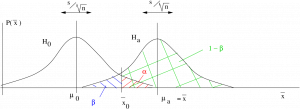
Case 1. Right tailed test:
![]()
where, In this case
![]()
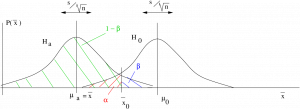
Case 2. Left tailed test:
![]()
where, In this case
![]()
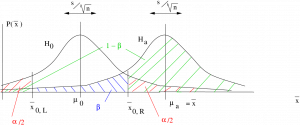
Case 3. Two-tailed test:
![]()
(a) ![]() in the right tail :
in the right tail :
(b) ![]() in the left tail:
in the left tail:
where, in both cases:
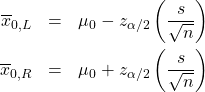
In both two-tailed cases, notice the small piece of ![]() area on the side of the
area on the side of the ![]() distribution on the opposite side from
distribution on the opposite side from ![]() . It turns out that the area of that small part is so incredibly small that we can take it to be zero. This will be obvious she we work through the examples. So the upshot is that going from a one-tailed test to a two-tailed test effectively decreases
. It turns out that the area of that small part is so incredibly small that we can take it to be zero. This will be obvious she we work through the examples. So the upshot is that going from a one-tailed test to a two-tailed test effectively decreases ![]() to
to ![]() which increases
which increases ![]() and decreases the power
and decreases the power ![]() . One-tailed tests have more power than two-tailed tests for the same
. One-tailed tests have more power than two-tailed tests for the same ![]() .
.
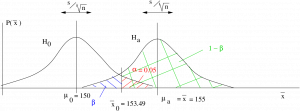
Example 13.1 Right tailed test.
Given :
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Find the observed power.
Step 1 : Look up ![]() in the t Distribution Table for a one-tailed test:
in the t Distribution Table for a one-tailed test: ![]() .
.
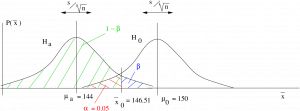
Step 2 : Compute :
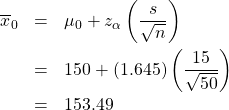
Step 3 : Draw picture :
Step 4 : Compute the ![]() -transform of
-transform of ![]() relative to
relative to ![]() :
:
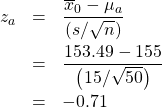
Step 5 : Look up the area ![]() in the Standard Normal Distribution Table. That area will be
in the Standard Normal Distribution Table. That area will be ![]() :
: ![]() , so
, so ![]() and power =
and power = ![]() 0.7611.
0.7611.
▢
Example 13.2 : Another right tailed test with the data the same as in Example 13.1 but with a smaller ![]() . This example shows how reducing
. This example shows how reducing ![]() will reduce the power. With reduced power, it is harder to reject
will reduce the power. With reduced power, it is harder to reject ![]() .
.
Given :
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Find the observed power.
Step 1 : Look up ![]() in t Distribution Table for a one-tailed test:
in t Distribution Table for a one-tailed test: ![]() .
.
Step 2 : Compute :
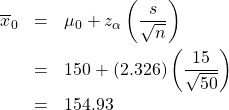
Step 3 : Draw picture :
Step 4 : Compute the ![]() -transform of
-transform of ![]() relative to
relative to ![]() :
:
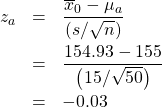
Step 5 : Look up the area ![]() in the Standard Normal Distribution Table. That area will be
in the Standard Normal Distribution Table. That area will be ![]() . So
. So ![]() and power =
and power = ![]() 0.5120 which is smaller than the power found in Example 13.1.
0.5120 which is smaller than the power found in Example 13.1.
▢
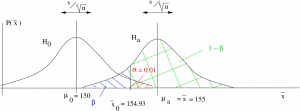
Example 13.3 : Another right tailed test with the data the same as in Example 13.2 but with larger ![]() . This example shows how increasing the sample size increases the power. This makes sense because more data is always better.
. This example shows how increasing the sample size increases the power. This makes sense because more data is always better.
Given :
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Find the observed power.
Step 1 : Look up ![]() in t Distribution Table for a one-tailed test:
in t Distribution Table for a one-tailed test: ![]() .
.
Step 2 : Compute :
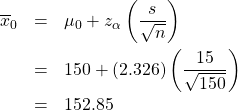
Step 3 : Draw picture :
Step 4 : Compute the ![]() -transform of
-transform of ![]() relative to
relative to ![]() :
:
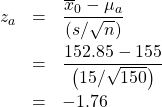
Step 5 : Look up the area ![]() in the Standard Normal Distribution Table. That area will be
in the Standard Normal Distribution Table. That area will be ![]() . So
. So ![]() and power =
and power = ![]() 0.9608 which is larger than the power found in Example 13.2.
0.9608 which is larger than the power found in Example 13.2.
▢
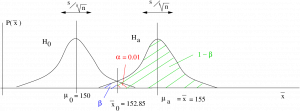
Example 13.4 : Another right tailed test with the data the same as in Example 13.3 but with a smaller value for ![]() which leads to a smaller effect size. This example shows how decreasing the effect size decreases the power. This makes sense because it is harder to detect a smaller signal.
which leads to a smaller effect size. This example shows how decreasing the effect size decreases the power. This makes sense because it is harder to detect a smaller signal.
Given :
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Find the observed power.
Step 1 : Look up ![]() in the t Distribution Table for a one-tailed test:
in the t Distribution Table for a one-tailed test: ![]() .
.
Step 2 : Compute :
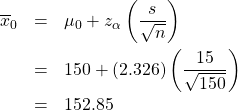
Step 3 : Draw picture :
Step 4 : Compute the ![]() -transform of
-transform of ![]() relative to
relative to ![]() :
:
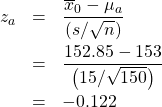
Step 5 : Look up the area ![]() in the Standard Normal Distribution Table. That area will be
in the Standard Normal Distribution Table. That area will be ![]() . So
. So ![]() and power =
and power = ![]() 0.5478 which is smaller than the power found in Example 13.3.
0.5478 which is smaller than the power found in Example 13.3.
▢
Example 13.5 : Left tailed test.
Given :
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Find the observed power.
Step 1 : Look up ![]() in the t Distribution Table for a one-tailed test:
in the t Distribution Table for a one-tailed test: ![]() .
.
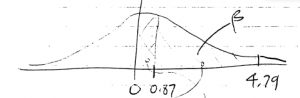
Step 2 : Compute :
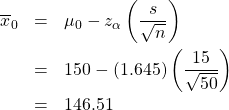
Step 3 : Draw picture :
Step 4 : Compute the ![]() -transform of
-transform of ![]() relative to
relative to ![]() :
:
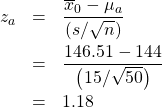
Step 5 : Look up the area ![]() in the Standard Normal Distribution Table. That area will be
in the Standard Normal Distribution Table. That area will be ![]() . So
. So ![]() and power =
and power = ![]() 0.8810.
0.8810.
▢
Example 13.6 : Two tailed ![]() -test with data the same as Example 13.5.
-test with data the same as Example 13.5.
Given :
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Find the observed power.
Step 1 : Look up ![]() in the t Distribution Table for a one-tailed test:
in the t Distribution Table for a one-tailed test: ![]() .
.
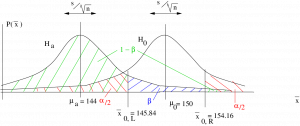
Step 2 : Compute:
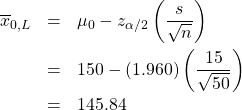
and
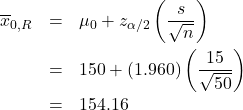
Step 3 : Draw picture :
Step 4 : Compute the ![]() -transform of
-transform of ![]() and
and ![]() relative to
relative to ![]() :
:
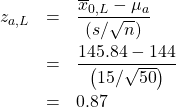
and
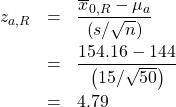
Step 5 : The two values, ![]() and
and ![]() appear on the
appear on the ![]() -distribution as :
-distribution as :
So using the areas ![]() from the Standard Normal Distribution Table we find
from the Standard Normal Distribution Table we find
![]()
Notice that ![]() is way the heck out there, it is higher than any
is way the heck out there, it is higher than any ![]() given in the Standard Normal Distribution Table. So
given in the Standard Normal Distribution Table. So ![]() is essentially 0.5; the tail area past
is essentially 0.5; the tail area past ![]() is essentially zero. So the effect of going to from a one-tail to a two-tail test is only felt by the size of the
is essentially zero. So the effect of going to from a one-tail to a two-tail test is only felt by the size of the ![]() critical region on the side where the test statistic (
critical region on the side where the test statistic (![]() here) is, which is half the size of the critical region in a one-tail test for a fixed
here) is, which is half the size of the critical region in a one-tail test for a fixed ![]() . In this case, then, the power =
. In this case, then, the power = ![]() 0.8078 which is smaller than the value found in Example 13.5.
0.8078 which is smaller than the value found in Example 13.5.
▢
Using observed power
As mentioned earlier, almost no one is interested in observed power because we must reject ![]() to compute it. People are interested in
to compute it. People are interested in ![]() and power only when you report a failure to reject
and power only when you report a failure to reject ![]() .
.
Suppose in the situation of Example 13.1 we wanted to find evidence that ![]() but measured
but measured ![]() (fail to reject
(fail to reject ![]() ). Then, with our given information of
). Then, with our given information of
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]()
we have
Based on the calculation we did in Example 13.1 we would report that we had a power of 0.7611 to detect an effect of ![]() but with
but with ![]() we were unable to detect
we were unable to detect ![]() .
.
- And a corollary of this will be that one-tailed tests are more powerful than two-tailed tests. ↵
- Effect size as defined in the Green and Salkind SPSS book would be
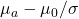 . But that quantity is not useful here, so we define effect size as the difference of the means for the purpose of this discussion on power. Reference: Green SB, Salkind NJ. Using SPSS for Windows and Macintosh: Analyzing and Understanding Data, new edition pretty much every year, Pearson, Toronto, circa 2005. ↵
. But that quantity is not useful here, so we define effect size as the difference of the means for the purpose of this discussion on power. Reference: Green SB, Salkind NJ. Using SPSS for Windows and Macintosh: Analyzing and Understanding Data, new edition pretty much every year, Pearson, Toronto, circa 2005. ↵