8. Confidence Intervals
8.5 Chi Squared Distribution
The ![]() (chi squared) distribution is a consequence of a random process based on the normal distribution. It is derived from the normal distribution as the result of the following stochastic process :
(chi squared) distribution is a consequence of a random process based on the normal distribution. It is derived from the normal distribution as the result of the following stochastic process :
- Suppose you have a population that has variance
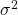 and is normally distributed.
and is normally distributed. - Take a sample of size
 from the population and compute
from the population and compute 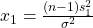 using the sample standard deviation
using the sample standard deviation 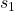 from that sample.
from that sample. - Put the sample back into the population.
- Take another sample of size
 from the population and compute
from the population and compute 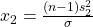 using the sample standard deviation
using the sample standard deviation 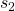 from that sample.
from that sample. - etc.
- The distribution of the values of
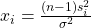 values will be a
values will be a 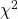 distribution with
distribution with 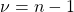 degrees of freedom.
degrees of freedom.
Like the ![]() -distributions, the
-distributions, the ![]() distributions are a family, see Figure 8.10.
distributions are a family, see Figure 8.10.
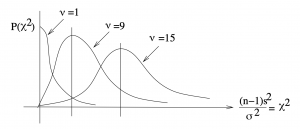
 distributions are enumerated by degrees of freedom.
distributions are enumerated by degrees of freedom.The ![]() distribution underlies why
distribution underlies why ![]() is the best estimate for
is the best estimate for ![]() . It mean, or expected value is
. It mean, or expected value is ![]() so the expected value of
so the expected value of ![]() is
is ![]() . The expected value of
. The expected value of ![]() in a random sample of size
in a random sample of size ![]() is not
is not ![]() .
.
Confidence Intervals on ![]() and
and ![]()
The ![]() distribution is already normalized in its definition through including
distribution is already normalized in its definition through including ![]() in its definition. Therefore no
in its definition. Therefore no ![]() -transforms are needed and we can work directly with a table that gives right tail areas under the
-transforms are needed and we can work directly with a table that gives right tail areas under the ![]() distribution. That table is the Chi-squared Distribution Table, in the Appendix, and it gives values of
distribution. That table is the Chi-squared Distribution Table, in the Appendix, and it gives values of ![]() for given values of area to the right of
for given values of area to the right of ![]() , see Figure 8.11.
, see Figure 8.11.
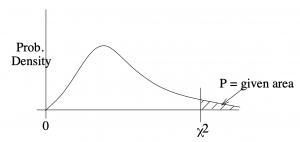
 associated with given right tail areas.
associated with given right tail areas.We’ll need ![]() and
and ![]() such that the tail areas are equal and such that the area between them is
such that the tail areas are equal and such that the area between them is ![]() , see Figure 8.12.
, see Figure 8.12.
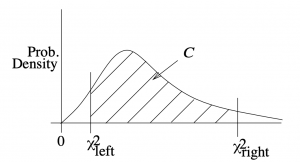
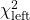 and
and 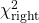 define the confidence region
define the confidence region 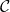 .
.Notation : Let’s call the ![]() in the Chi-squared Distribution Table
in the Chi-squared Distribution Table ![]() and let
and let ![]() be the table value that corresponds to
be the table value that corresponds to ![]() . In other words
. In other words ![]() is the
is the ![]() value that corresponds to a right tail area of
value that corresponds to a right tail area of ![]() .
.
So given ![]() , the appropriate
, the appropriate ![]() and
and ![]() are the following values from the Chi-squared Distribution Table:
are the following values from the Chi-squared Distribution Table:
![]()
![]()
Note the symmetry of the Chi-squared Distribution Table. If ![]() comes from the column 3 columns from the right edge of the table then
comes from the column 3 columns from the right edge of the table then ![]() comes from a column 3 columns from the left edge of the table. Only small and large areas appear in the table, there are no intermediate values.
comes from a column 3 columns from the left edge of the table. Only small and large areas appear in the table, there are no intermediate values.
Finally, the confidence interval for ![]() is given by
is given by
![]()
and for ![]() by:
by:
![Rendered by QuickLaTeX.com \[\sqrt{\frac{(n-1)s^2}{\chi^2_{\rm right}}} < \sigma < \sqrt{\frac{(n-1)s^2}{\chi^2_{\rm left}}}\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-f400d471088b5911f912d9f49cca956e_l3.png)
Where the ![]() distribution with
distribution with ![]() degrees of freedom (giving the line to use in the Chi-squared Distribution Table) is used.
degrees of freedom (giving the line to use in the Chi-squared Distribution Table) is used.
Example 8.5 : Find the 90![]() confidence interval on
confidence interval on ![]() and
and ![]() for the following data
for the following data
![]()
Solution : Compute, using your calculator :
![]()
![]()
From the Chi-squared Distribution Table, in the ![]() line, find :
line, find :
![]()
and
![]()
So
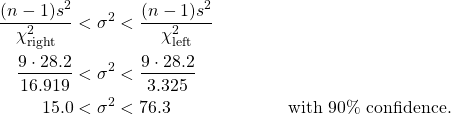
Taking square roots:
![]()
▢

