16. Non-parametric Tests

16.2 Median Sign Test

The median sign test is a test of a null hypothesis about the median, MD, of a population based on the binomial distribution. To use the test, every subject is assigned a score of +, 0 or - depending on whether their data point value is greater than, the same as or less than the H_{0} median.

Since the test is based on the binomial distribution, there are two cases we need to consider. One for small samples and one for large samples where the z approximation to the binomial distribution can be used.

Case 1 : small samples (n < 26). Here the test statistic is

    \[ X_{\mbox{test}} = \min [(\mbox{no. of $+$}), (\mbox{no. of $-$})] \]

and the critical statistic, X_{\mbox{crit}} comes from the Sign Test Critical Values Table for a given \alpha, 1 or 2 tailed test and a value for n_{s} where

    \[ n_{s} = (\mbox{no. of $+$}) + (\mbox{no. of $-$}) \]

Reject H_{0} if X_{\mbox{test}} \leq X_{\mbox{crit}}.

Case 2 : large samples (n \geq 26). With X_{\mbox{test}} as defined for case 1, the test statistic is

    \[ z_{\mbox{test}} = \frac{(X_{\mbox{test}} + 0.5) - (n/2)}{(\sqrt{n}/2)} \]

where

    \[ n = (\mbox{no. of $+$}) + (\mbox{no. of $0$}) + (\mbox{no. of $-$}) \neq n_{s} \]

the critical statistic is z_{\mbox{crit}} obtained in the usually way using either the Standard Normal Distribution Table or (recommended) the t Distribution Table. Reject H_{0} if z_{\mbox{test}} is in the critical region.

There are 3 sets of hypotheses about the null hypothesis median, M_{0} :

Two-tailed Left-tailed Right-tailed
H_{0}: \mbox{MD} = M_{0} H_{0}: \mbox{MD} \geq M_{0} H_{0}: \mbox{MD} \leq M_{0}
H_{1}: \mbox{MD} \neq M_{0} H_{1}: \mbox{MD} < M_{0} H_{1}: \mbox{MD} > M_{0}

Example 16.3 (Small sample size, case 1.).

Given the following snow cone sales data :

18  43  40  16  22
30  29  32  37  36
39  34  39  45  28
36  40  34  39  52

test the conjecture that the median snow cone sales is 40.

Solution.

0. Data reduction.

Reduce the data to +, 0 and - signs relative to M_{0} = 40 :

-  +  0  -  -
-  -  -  -  -
-  -  -  +  -
-  0  -  - +

so (no. of +) = 3, (no. of -) = 15 and n_{s} = 3 + 15 = 18.

1. Hypothesis.

    \begin{eqnarray*} H_{0} &:& \mbox{MD} = 40 \\ H_{1} &:& \mbox{MD} \neq 40 \\ \end{eqnarray*}

2. Critical statistic.

Using the Sign Test Critical Values Table with n_{s} = 18 and \alpha = 0.05 for a two-tailed test find

    \[ X_{\mbox{crit}} = 4 \]

3. Test statistic.

    \begin{eqnarray*} X_{\mbox{test}} & = & \min [(\mbox{no. of $+$}), (\mbox{no. of $-$})] \\ & = & \min [3,15] = 3 \end{eqnarray*}

4. Decision.

    \[(X_{\mbox{test}} = 3) < (X_{\mbox{crit}} = 4)\]

so reject H_{0}.

5. Interpretation.

There is enough evidence to reject the claim that the median number of snow cone sales is 40.

▢

Example 16.4 : (Large sample size, case 2.)

We wish to test the claim that the median lifetime of manufactured rubber washers is greater than or equal to 8 years. We are given the following data from a sample of 50 washers :

  • 21 washers in our sample last more than 8 years
  • 29 washers in our sample last less than 8 years
  • (none last exactly 8 years).

Solution.

0. Data reduction.

Label the washer that last longer than 8 years with a + and the others with a -. So (no. of +) = 21 and (no. of -) = 29.

1. Hypothesis

H_{0}: MD \geq 8 (claim)
H_{1}: MD < 8

2. Critical statistic.

Using the t Distribution Table, last (z) line, \alpha = 0.05 for a one-tailed test we find

    \[ z_{\mbox{crit}} = -1.645 \]

3. Test statistic.

    \begin{eqnarray*} X_{\mbox{test}} & = & \min [(\mbox{no. of $+$}), (\mbox{no. of $-$})] \\ & = & \min [21,29] = 21 \end{eqnarray*}

so

    \begin{eqnarray*} z_{\mbox{test}} & = & \frac{(X_{\mbox{test}} + 0.5) - (n/2)}{(\sqrt{n}/2)}\\ & = & \frac{(21 + 0.5) - (50/2)}{(\sqrt{50}/2)}\\ & = & \frac{21.5 - 25}{3.5355}\\ & = & -0.99 \end{eqnarray*}

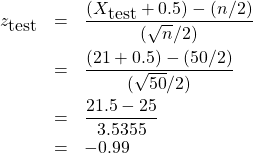
4. Decision.

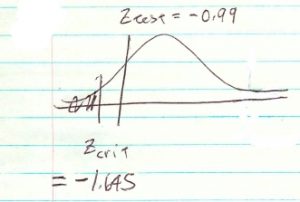
Do not reject H_{0}.

5. Interpretation.

There is not enough evidence, at \alpha = 0.05, to say that washers last less that 8 years.

▢

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book