14. Correlation and Regression

14.6 r² and the Standard Error of the Estimate of y′

Consider the deviations :

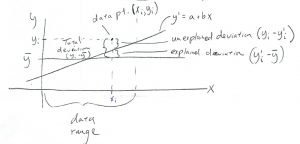
Looking at the picture we see that

    \begin{eqnarray*} \textrm{total deviation} & = & \textrm{explained deviation + unexplained deviation}\\ (y_{i} - \overline{y}_{i}) & = & (y^{\prime}_{i} - \overline{y}_{i}) + (y_{i} - y^{\prime}_{i}) \end{eqnarray*}

Remember that variance is the sum of the squared deviations (divided by degrees of freedom), so squaring the above and summing gives:

    \[ \sum_{i=1}^{n} (y_{i} - \overline{y}_{i})^{2} = \sum_{i=1}^{n} (y^{\prime}_{i} - \overline{y}_{i})^{2} + \sum_{i=1}^{n} (y_{i} - y^{\prime}_{i})^{2} \]

(the cross terms all cancel because y^{\prime} is the least square solution and a = \overline{y} - b \overline{x}, see Section 14.6.1, below, for details). This is also a sum of squares statement:

    \[ \mbox{SS}_{T} = \mbox{SS}_{R} + \mbox{SS}_{E} \]

where SS_{E} = \sum (y_{i} - y^{\prime}_{i})^{2}, SS_{T} = \sum (y_{i} - \overline{y})^{2} and SS_{R} = \sum (y^{\prime}_{i} - \overline{y})^{2} are the sum of squares — error, sum of squares — total and sum of squares — regression (explained) respectively.

Dividing by the degrees of freedom, which is n-2 in this {\em bivariate} situation, we get:

    \begin{eqnarray*} \frac{\sum (y_{i} - \overline{y}_{i})^{2}}{n-2} & = & \frac{\sum (y^{\prime}_{i} - \overline{y}_{i})^{2}}{n-2} + \frac{\sum (y_{i} - y^{\prime}_{i})^{2}}{n-2} \\ \mbox{total variance} & = & \mbox{explained variance} + \mbox{unexplained variance} \\ & = & \mbox{signal (or model)} + \mbox{noise} \end{eqnarray*}

It turns out that

    \[ r^{2} = \frac{\mbox{explained variance}}{\mbox{total variance}} = \frac{ \mbox{SS}_{R} }{ \mbox{SS}_{T} } \]

The quantity r^{2} is called the coefficient of determination and gives the the fraction of variance explained by the model (here the model is the equation of a line). The quantity r^{2} appears with many statistical models. For example with ANOVA it turns out that the “effect size” eta-squared is the fraction of variance explained by the ANOVA model[1], \eta^{2} = r^{2}.

The standard error of the estimate is the standard deviation of the noise (the square root of the unexplained variance) and is given by

    \[ s_{\mbox{est}} = \sqrt{\frac{\sum (y - y^{\prime})^{2} }{n-2} } = \sqrt{\frac{\sum y^{2} - a \sum y - b \sum xy}{n-2} } \]

Example 14.4: Continuing with the data of Example 14.3, we had

    \[ \sum y = 511 \;\;\; \sum y^{2} = 38993 \;\;\; \sum xy = 3745 \;\;\; a = 102.493 \;\;\; b = -3.622 \;\;\; n=7 \]

so

    \begin{eqnarray*} s_{\mbox{est}} & = & \sqrt{\frac{(38993) - (102.493)(511) - (-3.622)(3745)}{5} } \\ s_{\mbox{est}} & = & \sqrt{\frac{38993 - 52373.923 + 13564.39}{5} } \\ s_{\mbox{est}} & = & 6.06 \end{eqnarray*}

▢

Here is a graphical interpretation of s_{\mbox{est}} :

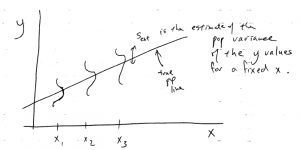
The assumption for computing confidence intervals for is that s_{\mbox{est}} is independent of x. This is the assumption of homoscedasticity. You can think of the regression situation as a generalized one-way ANOVA where instead of having a finite number of discrete populations for the IV, we have an infinite number of (continuous) populations. All the populations have the same variance \sigma^{2} (and they are assumed to be normal) and s_{\mbox{est}^{2}} is the pooled estimate of that variance.

14.6.1: **Details: from deviations to variances

Squaring both sides of

    \[ (y_{i} - \overline{y}_{i}) = (y^{\prime}_{i} - \overline{y}_{i}) + (y_{i} - y^{\prime}_{i}) \]

and summing gives

    \[ \sum (y_{i} - \overline{y}_{i})^{2} = \sum (y^{\prime}_{i} - \overline{y}_{i})^{2} + \sum (y_{i} - y^{\prime}_{i})^{2} + \sum 2 (y^{\prime}_{i} - \overline{y})(y_{i} - y^{\prime}_{i}) \]

Working on that cross term, using a = \overline{y} - b \overline{x}, we get

    \begin{eqnarray*} \sum 2 (y^{\prime}_{i} - \overline{y})(y_{i} - y^{\prime}_{i}) & = & \sum 2((\overline{y} - b \overline{x} + b x_{i}) - \overline{y})(y_{i} - y^{\prime}_{i}) \\ & = & \sum 2((\overline{y} + b(x_{i} - \overline{x}))-\overline{y})(y_{i} - y^{\prime}_{i}) \\ & = & \sum 2(b(x_{i}- \overline{x}))(y_{i} - y^{\prime}_{i}) \\ & = & \sum 2 b (x_{i} - \overline{x})(y_{i} - (\overline{y} + b(x_{i} - \overline{x}))) \\ & = & \sum 2 b ((y_{i} - \overline{y})(x_{i} - \overline{x}) - b(x_{i} - \overline{x})^{2}) \\ & = & 2 b \sum ((y_{i} - \overline{y})(x_{i} - \overline{x}) - (y_{i} - \overline{y})(x_{i} - \overline{x})) = 0 \end{eqnarray*}

where

    \[ b = \frac{\sum (x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum(x_{i}-\overline{x})^{2}} \]

was used in the last line.

 

  1. In ANOVA the ``model'' is the difference of means between the groups. We will see more about this aspect of ANOVA in Chapter 17. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book