14. Correlation and Regression
14.10 Multiple Regression
Multiple regression is to the linear regression we just covered as one-way ANOVA is to ![]() -way ANOVA. In
-way ANOVA. In ![]() -way ANOVA we have one DV and
-way ANOVA we have one DV and ![]() discrete IVs. With multiple regression we have one DV (univariate) and
discrete IVs. With multiple regression we have one DV (univariate) and ![]() continuous IVs. We will label the DV with
continuous IVs. We will label the DV with ![]() and the IVs with
and the IVs with ![]() . The idea is to predict
. The idea is to predict ![]() with
with ![]() via
via
![]()
or, using summation notation
![Rendered by QuickLaTeX.com \[y^{\prime} = a +\sum_{j=1}^{k} b_{j} x_{j}\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-daa390f4ab9c3b09b566dec79f30b537_l3.png)
Sometimes we (and SPSS) write ![]() . The explicit formula for the coefficients
. The explicit formula for the coefficients ![]() and
and ![]() are long so we won’t give them here but, instead, we will rely on SPSS to compute the coefficients for us. Just the same, we should remember that the coefficients are computed using the least squares method, where the sum of the squared deviations is minimized. That is,
are long so we won’t give them here but, instead, we will rely on SPSS to compute the coefficients for us. Just the same, we should remember that the coefficients are computed using the least squares method, where the sum of the squared deviations is minimized. That is, ![]() and the
and the ![]() are such that
are such that
![Rendered by QuickLaTeX.com \begin{eqnarray*} E & = & \sum_{i=1}^{n} (y_{i} - y^{\prime}_{i})^{2} \\ & = & \sum_{i=1}^{n} (y_{i} - [a + \sum_{j=1}^{k} b_{j} x_{ji}])^{2} \end{eqnarray*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-44a599f8b3cd6a1036292d98ab8ef336_l3.png)
is minimized. (Here we are using ![]() to represent data point
to represent data point ![]() .) If you like calculus and have a few minutes to spare, the equations for
.) If you like calculus and have a few minutes to spare, the equations for ![]() and the
and the ![]() can be found by solving:
can be found by solving:
![]()
for ![]() and the
and the ![]() . The result will contain al the familiar terms like
. The result will contain al the familiar terms like ![]() ,
, ![]() , etc. It also turns out that the “normal equations” for
, etc. It also turns out that the “normal equations” for ![]() and the
and the ![]() that result have a pattern that can be captured with a simple linear algebra equation that we will see in Chapter 17.
that result have a pattern that can be captured with a simple linear algebra equation that we will see in Chapter 17.
Some terminology: the ![]() (including
(including ![]() ) are known as partial regression coefficients.
) are known as partial regression coefficients.
14.10.1: Multiple regression coefficient, r
An overall correlation coefficient, ![]() , can be computed using pairwise bivariate correlation coefficients as defined in the previous Section 14.2. This overall correlation is defined as
, can be computed using pairwise bivariate correlation coefficients as defined in the previous Section 14.2. This overall correlation is defined as ![]() , the bivariate correlation coefficient of the predicted values
, the bivariate correlation coefficient of the predicted values ![]() versus the data
versus the data ![]() . For the case of 2 IVs, the formula is
. For the case of 2 IVs, the formula is
![Rendered by QuickLaTeX.com \[ r = \sqrt{\frac{r_{y x_{1}}^{2} + r^{2}_{y x_{2}} - 2 r_{y x_{1}} r_{y x_{2}} r_{x_{1} x_{2}} }{1 - r^{2}_{x_{1} x_{2}}}} \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-e99c7d03ecfd4705430b96106ca5be0d_l3.png)
where ![]() is the bivariate correlation coefficient between
is the bivariate correlation coefficient between ![]() and
and ![]() , etc. It is true that
, etc. It is true that ![]() as with the bivariate
as with the bivariate ![]() .
.
Example 14.6 : Suppose that you have used SPSS to obtain the regression equation
![]()
for the following data :
| Student | GPA, |
Age, |
Score, |
||||||
| A | 3.2 | 22 | 550 | 10.24 | 484 | 302500 | 1760 | 12100 | 70.4 |
| B | 2.7 | 27 | 570 | 7.29 | 729 | 324900 | 1539 | 15390 | 72.9 |
| C | 2.5 | 24 | 525 | 6.25 | 576 | 275625 | 1312.5 | 12600 | 60 |
| D | 3.4 | 28 | 670 | 11.56 | 784 | 448900 | 2278 | 18760 | 95.2 |
| E | 2.2 | 23 | 490 | 4.84 | 529 | 240100 | 1078 | 11270 | 50.6 |
Compute the multiple correlation coefficient.
Solution :
First we need to compute the pairwise correlations ![]() ,
, ![]() , and
, and ![]() . (Note that
. (Note that ![]() =
= ![]() , etc. because the correlation matrix is symmetric.)
, etc. because the correlation matrix is symmetric.)
![Rendered by QuickLaTeX.com \begin{eqnarray*} r_{x_{1}y} & = & \frac{n(\sum x_{1} y) - (\sum x_{1} ) (\sum y )}{\sqrt{[n (\sum x_{1}^{2}) - (\sum x_{1})^{2}] [n (\sum y^{2}) - (\sum y)^{2}}]}\\ & = & \frac{5(7967.5) - (14 ) (2805 )}{\sqrt{[5 (40.18) - (14)^{2}] [5 (1592025) - (2805)^{2}}]}\\ & = & 0.845 \end{eqnarray*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-f2bbe656e45f87cb2d868e539d669f27_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} r_{x_{2}y} & = & \frac{n(\sum x_{2} y) - (\sum x_{2} ) (\sum y )}{\sqrt{[n (\sum x_{2}^{2}) - (\sum x_{2})^{2}] [n (\sum y^{2}) - (\sum y)^{2}}]}\\ & = & \frac{5(70120) - (124 ) (2805 )}{\sqrt{[5 (3102) - (124)^{2}] [5 (1592025) - (2805)^{2}}]}\\ & = & 0.791 \end{eqnarray*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-d3e738b287071b2a040aa4a2ef63edef_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} r_{x_{1}x_{2}} & = & \frac{n(\sum x_{1} x_{2}) - (\sum x_{1} ) (\sum x_{2} )}{\sqrt{[n (\sum x_{1}^{2}) - (\sum x_{1})^{2}] [n (\sum x_{2}^{2}) - (\sum x_{2})^{2}}]}\\ & = & \frac{5(349.1) - (14 ) (124)}{\sqrt{[5 (40.18) - (14)^{2}] [5 (3102) - (124)^{2}}]}\\ & = & 0.371 \end{eqnarray*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-075ef194a2122b3250bab3c85fcf4c0d_l3.png)
Now use these in :
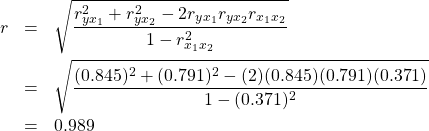
▢
14.10.2: Significance of r
Here we want to test the hypotheses :
![]()
where ![]() is the population multiple regression correlation coefficient.
is the population multiple regression correlation coefficient.
To test the hypothesis we use
![]()
with
![]()
here:

(Note: This “![]() -test” is similar to but not the same as the “ANOVA” output given by SPSS when you run a regression.)
-test” is similar to but not the same as the “ANOVA” output given by SPSS when you run a regression.)
Example 14.7 : Continuing with Example 14.6, test the significance of ![]() .
.
Solution :
1. Hypotheses.
![]()
2. Critical statistic. From the Rank Correlation Coefficient Critical Values Table (i.e., the critical values for the Spearman correlation) with
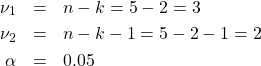
find
![]()
3. Test statistic.
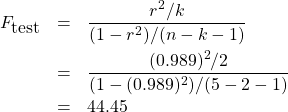
4. Decision.
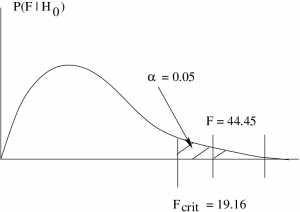
Reject ![]() .
.
5. Interpretation.
![]() is significant.
is significant.
▢
14.10.3: Other descriptions of correlation
- Coefficient of multiple determination:
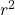 . This quantity still has the interpretation as fraction of variance explained by the (multiple regression) model.
. This quantity still has the interpretation as fraction of variance explained by the (multiple regression) model. - Adjusted
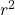 :
:
![Rendered by QuickLaTeX.com \[ r^{2}_{\mbox{adj}} = 1 -\ \left[ \frac{(1-r^{2})(n-1)}{n-k-1} \right] \]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-1c123c03b06f050825ce7a3346d5ed40_l3.png)
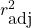 gives a better (unbiased) estimate of the population value for
gives a better (unbiased) estimate of the population value for 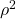 by correcting for degrees of freedom just as the sample
by correcting for degrees of freedom just as the sample 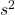 with its degrees of freedom equal to
with its degrees of freedom equal to  gives an unbiased estimate of the population
gives an unbiased estimate of the population 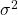 .
.
Example 14.8 : Continuing Example 14.6, we had ![]() so
so
![]()
and
![Rendered by QuickLaTeX.com \begin{eqnarray*} r^{2}_{\mbox{adj}} & = & 1 -\ \left[ \frac{(1-r^{2})(n-1)}{n-k-1} \right] \\ r^{2}_{\mbox{adj}} & = & 1 -\ \left[ \frac{(1-0.978)(5-1)}{5-2-1} \right] \\ & = & 0.956 \end{eqnarray*}](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-b5d5ada7832af5e06c37dcd98e0299d0_l3.png)
▢

