11. Comparing Proportions
11.2 Confidence Interval for the Difference between Two Proportions
The form of the confidence interval is
![]()
with
![]()
where, as usual you can get ![]() from the last line of the t Distribution Table.
from the last line of the t Distribution Table.
Example 11.2 : Using the data from Example 11.1, find the 95![]() confidence interval for
confidence interval for ![]() .
.
Solution : The relevant numbers from Example 11.1 are: ![]() ,
, ![]() ,
, ![]() and
and ![]() ,
, ![]() ,
, ![]() .
.
Compute (after finding ![]() from the t Distribution Table)
from the t Distribution Table)
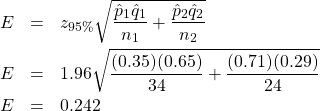
and
![]()
So
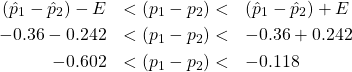
with 95![]() confidence. (Note that this corresponds with the rejection of
confidence. (Note that this corresponds with the rejection of ![]() in Example 11.1 since 0 is not in the confidence interval.)
in Example 11.1 since 0 is not in the confidence interval.)
▢

