10. Comparing Two Population Means
10.3 Difference between Two Variances – the F Distributions
Here we have to assume that the two populations (as opposed to sample mean distributions) have a distribution that is almost normal as shown in Figure 10.2.
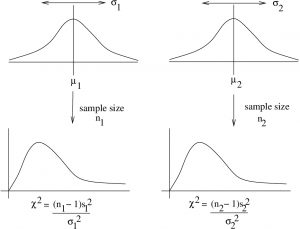
Figure 10.2: Two normal populations lead to two ![]() distributions that represent distributions of sample variances. The
distributions that represent distributions of sample variances. The ![]() distribution results when you build up a distribution of the ratio of the two
distribution results when you build up a distribution of the ratio of the two ![]() sample values.
sample values.
The ratio ![]() follows an
follows an ![]() -distribution if
-distribution if ![]() . That
. That ![]() distribution has two degrees of freedom: one for the numerator (d.f.N. or
distribution has two degrees of freedom: one for the numerator (d.f.N. or ![]() ) and one for the denominator (d.f.D. or
) and one for the denominator (d.f.D. or ![]() ). So we denote the distribution more specifically as
). So we denote the distribution more specifically as ![]() . For the case of Figure 10.2,
. For the case of Figure 10.2, ![]() and
and ![]() . The
. The ![]() ratio, in general is the result of the following stochastic process. Let
ratio, in general is the result of the following stochastic process. Let ![]() be random variable produced by a stochastic process with a
be random variable produced by a stochastic process with a ![]() distribution and let
distribution and let ![]() be random variable produced by a stochastic process with a
be random variable produced by a stochastic process with a ![]() distribution. Then the random variable
distribution. Then the random variable ![]() will, by definition, have a
will, by definition, have a ![]() distribution.
distribution.
The exact shape of the ![]() distribution depends on the choice of
distribution depends on the choice of ![]() and
and ![]() , But it roughly looks like a
, But it roughly looks like a ![]() distribution as shown in Figure 10.3.
distribution as shown in Figure 10.3.
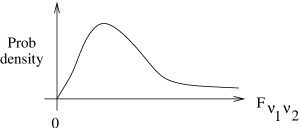
 distribution.
distribution.![]() and
and ![]() are related :
are related :
![]()
so the ![]() statistic can be viewed as a special case of the
statistic can be viewed as a special case of the ![]() statistic.
statistic.
For comparing variances, we are interested in the follow hypotheses pairs :
| Right-tailed | Left-tailed | Two-tailed |
We’ll always compare variances (![]() ) and not standard deviations (
) and not standard deviations (![]() ) to keep life simple.
) to keep life simple.
The test statistic is
![]()
where (for finding the critical statistic), ![]() and
and ![]() .
.
Note that ![]() when
when ![]() , a fact you can use to get a feel for the meaning of this test statistic.
, a fact you can use to get a feel for the meaning of this test statistic.
Values for the various ![]() critical values are given in the F Distribution Table in the Appendix. We will denote a critical value of
critical values are given in the F Distribution Table in the Appendix. We will denote a critical value of ![]() with the notation :
with the notation :
![]()
Where:
![]() = Type I error rate
= Type I error rate
![]() = d.f.N.
= d.f.N.
![]() = d.f.D.
= d.f.D.
The F Distribution Table gives critical values for small right tail areas only. This means that they are useless for a left-tailed test. But that does not mean we cannot do a left-tail test. A left-tail test is easily converted into a right tail test by switching the assignments of populations 1 and 2. To get the assignments correct in the first place then, always define populations 1 and 2 so that ![]() . Assign population 1 so that it has the largest sample variance. Do this even for a two-tail test because we will have no idea what
. Assign population 1 so that it has the largest sample variance. Do this even for a two-tail test because we will have no idea what ![]() on the left side of the distribution is.
on the left side of the distribution is.
Example 10.3 : Given the following data for smokers and non-smokers (maybe its about some sort of disease occurrence, who cares, let’s focus on dealing with the numbers), test if the population variances are equal or not at ![]() .
.
| Smokers | Nonsmokers |
Note that ![]() so we’re good to go.
so we’re good to go.
Solution :
1. Hypothesis.
![]()
2. Critical statistic.
Use the F Distribution Table; it is a bunch of tables labeled by “![]() ” that we will designate at
” that we will designate at ![]() , the table values that signify right tail areas. Since this is a two-tail test, we need
, the table values that signify right tail areas. Since this is a two-tail test, we need ![]() . Next we need the degrees of freedom:
. Next we need the degrees of freedom:
![]()
![]()
So the critical statistic is
![]()
3. Test statistic.
![]()
![]()
With this test statistic, we can estimate the ![]() -value using the F Distribution Table. To find
-value using the F Distribution Table. To find ![]() , look up all the numbers with d.f.N = 25 and d.f.N = 17 (24
, look up all the numbers with d.f.N = 25 and d.f.N = 17 (24 ![]() 17 are the closest in the tables so use those) in all the the F Distribution Table and form your own table. For each column in your table record
17 are the closest in the tables so use those) in all the the F Distribution Table and form your own table. For each column in your table record ![]() and the
and the ![]() value corresponding to the degrees of freedom of interest. Again,
value corresponding to the degrees of freedom of interest. Again, ![]() corresponds to
corresponds to ![]() for a two-tailed test. So make a row above the
for a two-tailed test. So make a row above the ![]() row with
row with ![]() . (For a one-tailed test, we would put
. (For a one-tailed test, we would put ![]() .)
.)
| 0.20 0.10 0.05 0.02 0.01 0.10 0.05 0.025 0.01 0.005 |
|
| 1.84 2.19 2.56 3.08 3.51 3.6 is over here somewhere so |
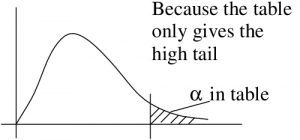
Notice how we put an upper limit on ![]() because
because ![]() was larger than all the
was larger than all the ![]() values in our little table.
values in our little table.
Let’s take a graphical look at why we use ![]() in the little table and
in the little table and ![]() for finding
for finding ![]() for two tailed tests :
for two tailed tests :
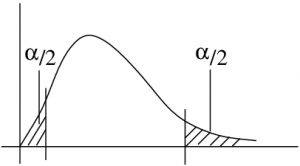
But in a two-tailed test we want ![]() split on both sides:
split on both sides:
4. Decision.
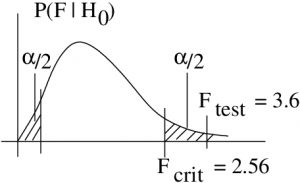
Reject ![]() . The
. The ![]() -value estimate supports this :
-value estimate supports this :
![]()
5. Interpretation.
There is enough evidence to conclude, at ![]() with an
with an ![]() -test, that the variance of the smoker population is different from the non-smoker population.
-test, that the variance of the smoker population is different from the non-smoker population.
▢

