10.10 SPSS Lesson 7: Paired Sample t-Test

Gordon E. Sarty

10. Comparing Two Population Means

10.10 SPSS Lesson 7: Paired Sample t-Test

To follow along, load in the Data Set “Methadone.sav”:

SPSS screenshot © International Business Machines Corporation.

As set up, the file has two dependent variables. This “within subjects” dataset is fundamentally multivariate. When we did the paired $t$ -test by hand we converted the multivariate data to univariate data by taking differences. SPSS will do the differences behind the scene and you won’t actually see them. Run the $t$ -test by picking Analyze $\rightarrow$ Compare Means $\rightarrow$ Paired -Samples T-Test:

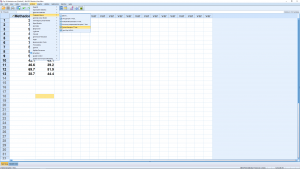
Move the two variables into Pair 1 and hit OK (Options again allows you to specify a confidence intervals percentage):

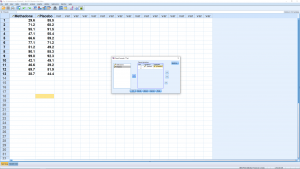
The output is:

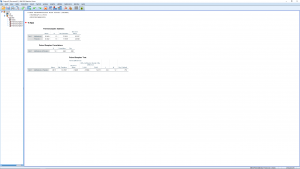
The first two tables are descriptive statistics. The last table gives the stuff we want: $\overline{D} = 0.9615$ , $s_{D} = 10.7067$ , the confidence interval

(10.11) $\begin{equation*} -5.5084< \mu_{D} < 7.4315, \end{equation*}$

$t_{\rm test} = 0.324$ , $\nu = 12$ and $p = 0.002$ for the two-tailed hypotheses pair

$H_{0}: & \mu_{D} = 0$

(10.12) $\begin{equation*} H_{1}: & \mu_{D} \neq 0. \end{equation*}$

The very low $p$ -value (0 in this case) and the absence of 0 in the confidence interval guide us to reject $H_{0}$ , the differences are significantly different from zero.