Isotope Pairs

Originally, fossils only provided us with relative ages because, although early paleontologists understood biological succession, they did not know the absolute ages of the different organisms. It was only in the early part of the 20th century, when isotopic dating methods were first applied, that it became possible to discover the absolute ages of the rocks containing fossils. In most cases, we cannot use isotopic techniques to directly date fossils or the sedimentary rocks in which they are found, but we can constrain their ages by dating igneous rocks that cut across sedimentary rocks, or volcanic ash layers that lie within sedimentary layers.

Isotopic dating of rocks, or the minerals within them, is based upon the fact that we know the decay rates of certain unstable isotopes of elements, and that these decay rates have been constant throughout geological time. It is also based on the premise that when the atoms of an element decay within a mineral or a rock, they remain trapped in the mineral or rock, and do not escape.

One of the isotope pairs commonly used to date rocks is the decay of ⁴⁰K to ⁴⁰Ar  (potassium-40 to argon-40). ⁴⁰K is a radioactive isotope of potassium that is present in very small amounts in all minerals that contain potassium. It has a half-life of 1.3 billion years, meaning that over a period of 1.3 Ga one-half of the ⁴⁰K atoms in a mineral or rock will decay to ⁴⁰Ar, and over the next 1.3 Ga one-half of the remaining atoms will decay, and so forth (Figure 19.18). ⁴⁰K is called the parent isotope, and ⁴⁰Ar the daughter isotope, as the parent gives way to the daughter during radioactive decay.

In order to use the K-Ar dating technique, we need to have an igneous or metamorphic rock that includes a potassium-bearing mineral. One good example is granite, which contains the mineral potassium feldspar (Figure 19.19). Potassium feldspar does not contain any argon when it forms. Over time, the ⁴⁰K in the feldspar decays to ⁴⁰Ar. The atoms of ⁴⁰Ar remain embedded within the crystal, unless the rock is subjected to high temperatures after it forms. The sample must be analyzed using a very sensitive mass-spectrometer, which can detect the differences between the masses of atoms, and can therefore distinguish between ⁴⁰K and the much more abundant ³⁹K. The minerals biotite and hornblende are also commonly used for K-Ar dating.

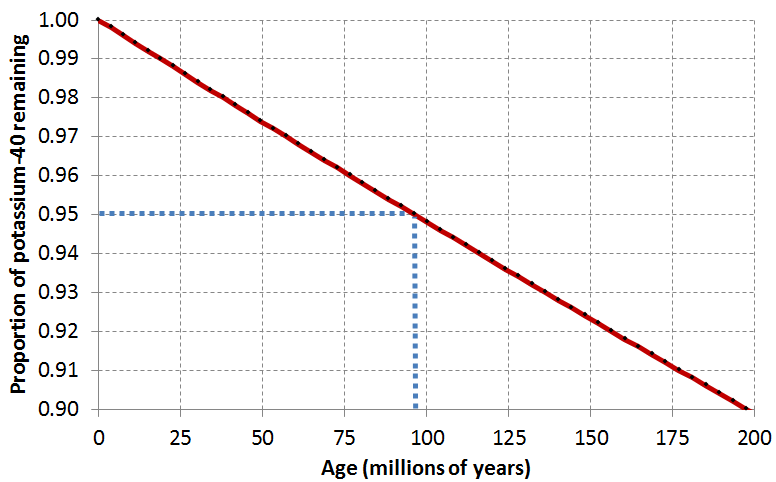
There are many isotope pairs that can be employed in dating igneous and metamorphic rocks (see Table 19.2), each with its strengths and weaknesses. In the above example, the daughter isotope ⁴⁰Ar is naturally a gas, and can escape the potassium feldspar quite easily if the feldspar is exposed to heating during metamorphism, or interaction with hydrothermal fluids. Hence we must closely examine the feldspar mineral to determine if there is any evidence of alteration. If some ⁴⁰Ar has been lost, but the sample is dated anyway, an age that is too young will be calculated.

Each parent isotope has a certain half-life, which ranges from microseconds to billions of years, depending upon the isotope. In dating rocks, we need to select an isotope pair with a parent isotope that has a reasonable half-life. This means that the half-life must not be too short or too long. If the half-life is too short, then most of the parent isotope will have decayed to form the daughter isotope. If we cannot measure the amount of parent isotope very accurately, which will be impossible to do if there is only the tiniest amount of parent isotope left, our calculated age will have huge errors associated with it. The same applies if the half-life is too long. In this case, very little of the daughter isotope will have formed, and our inability to measure the small amount of daughter isotope accurately will again result in huge errors in our calculated age.

Another complicating factor is whether the mineral of interest incorporated any of the daughter isotope into its structure at the time of formation. When we select a mineral and an isotope pair to date that mineral, we make the assumption that all of the daughter isotope we find in the mineral was produced in the mineral by radioactive decay of the parent isotope. But if the mineral formed with some daughter isotope already present in its structure, then the age we calculate will be too old.

A more robust mineral to use to date certain types of igneous and metamorphic rocks is zircon. Zircon is a mineral that incorporates uranium into its structure at the time of formation. One of the isotopes of uranium decays to lead with a long half-life (see Table 19.2). Zircon is a mineral of choice for dating because it takes no lead into its structure when it forms, so any lead present is due entirely to the radioactive decay of the uranium parent. Another reason is because zircon is a very resistant mineral. It can handle exposure to hydrothermal fluids, and all but the highest grades of metamorphism, and not lose any of the parent or daughter isotopes. Hence the age that we calculate tends to be very accurate. One drawback is that zircon tends to form only in felsic igneous rocks. Hence if we are trying to date a mafic igneous rock, we must choose a different mineral.

The Meaning of a Radiometric Date

When we employ isotopic methods on minerals we are measuring an age date. Generally, an age date refers to the time since a mineral crystallized from molten rock (magma or lava). This is when the elements that make up the mineral get locked into the mineral’s structure. But as we have already seen, elevated temperatures can cause elements to escape from a mineral, without the mineral melting. Hence when we date a mineral, we may be dating the time since the mineral crystallized from a melt, or the time since the mineral last experienced a period of heating above its Curie point, which is the temperature beyond which the mineral is able to lose (or gain) elements from its structure, without melting. So we have to know something about the rock before we forge ahead to measure an age. We may choose a mineral and isotope pair that are very resistant to metamorphism, so that we can “see through” the metamorphism, and determine the original age that the mineral crystallized from a melt. Or we may be interested in the age of the metamorphic event itself, so choose a mineral and isotope pair that is susceptible to resetting the isotopic clock during metamorphism (such as by losing all of the daughter isotope).

Absolute age dating is a powerful tool for unraveling the geological history of a region, but we have seen that we must ultimately rely upon igneous rocks (that may have later metamorphosed) for the minerals that we are able to date (see the next section for issues with dating sedimentary rocks directly). Another issue with absolute age dating is that it is expensive, with a single analysis costing several hundreds of dollars. Hence geologists never forget their relative age dating principles, and are always applying them in the field to determine the sequence of events that formed the rocks in a region.

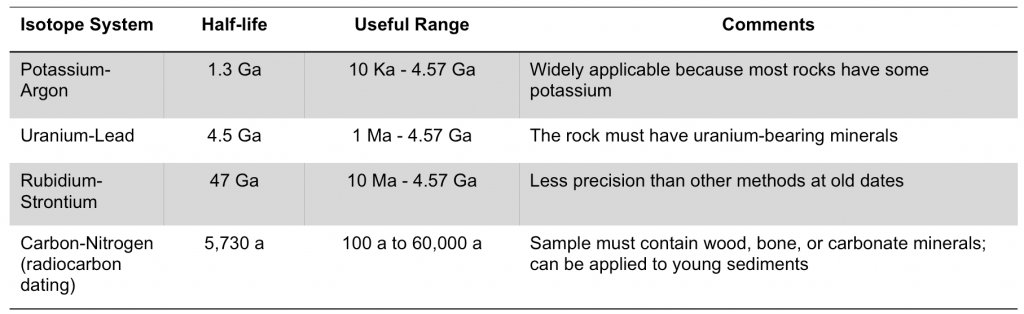
Exercise: Combining Absolute Ages with Relative Dating

The age dates for three igneous rock layers are given. Use relative dating techniques to determine the age ranges for the sets of sedimentary units A, B, and C.

Isotope Dating Techniques and Sedimentary Rocks

A clastic sedimentary rock (e.g., conglomerate, Figure 19.21) is made up of older rock and mineral fragments. These fragments were derived from weathering and erosion of pre-existing rocks. The process of forming a sedimentary rock from sediments generally occurs at low temperatures, so the minerals are not heated beyond their Curie points. Hence the minerals still preserve their original ages (either igneous crystallization age, or a metamorphic age).

In almost all cases, the fragments have come from a range of source rocks that all formed at different times. If we dated a number of individual grains in the sedimentary rock, we would likely get a range of different dates, all older than the age of the sedimentary rock. The most that such ages gleaned from a sedimentary rock can tell us is a maximum age of the sedimentary rock. It might be possible to date some chemical sedimentary rocks isotopically, but there are no useful isotopes that can be used on old chemical sedimentary rocks.

Radiocarbon Dating

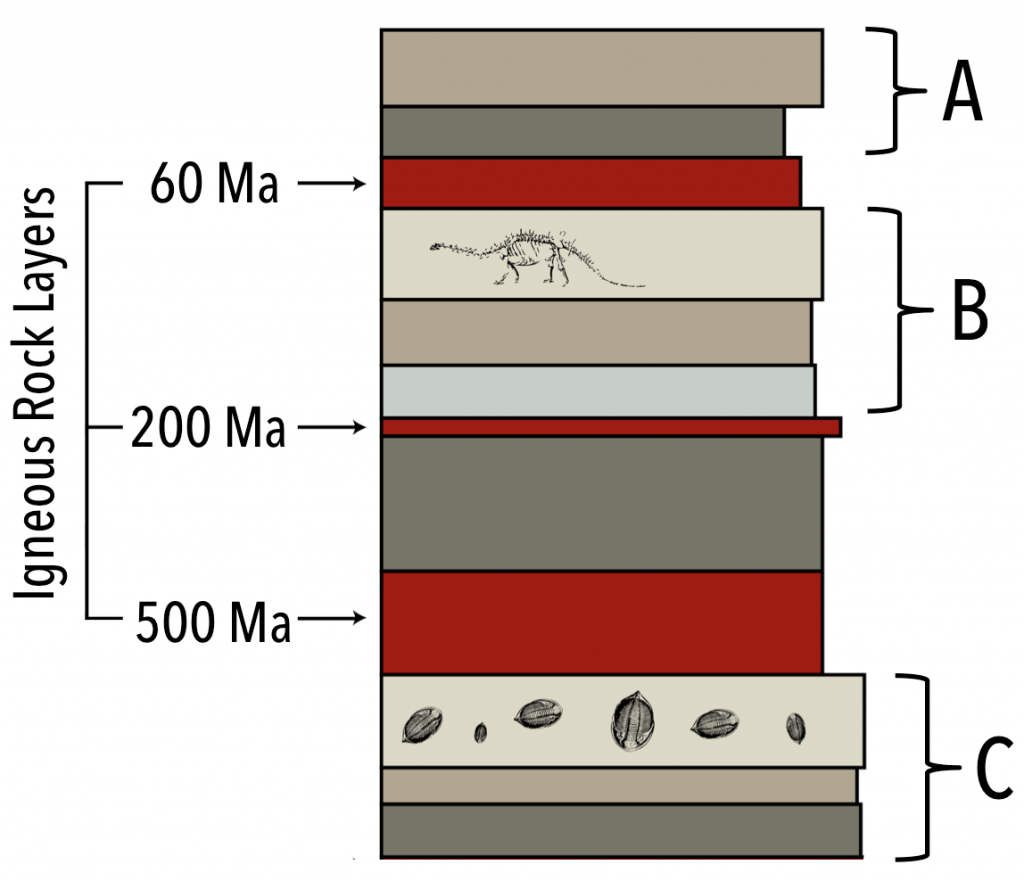
Radiocarbon dating (using ¹⁴C) can be applied to many geological materials, including sediment and sedimentary rocks, but only if the materials in question are younger than ~60 ka, and contain organic material. Beyond this time, there is so little ¹⁴C left that it cannot be measured accurately, and the resulting age dates are hence unreliable. Fragments of wood incorporated into young sediment are good candidates for carbon dating, and this technique has been used widely in studies involving late Pleistocene glaciers and glacial sediments. Figure 19.22 shows radiocarbon dates from wood fragments in glacial sediments have been used to estimate the time of the last glacial advance along the Strait of Georgia.

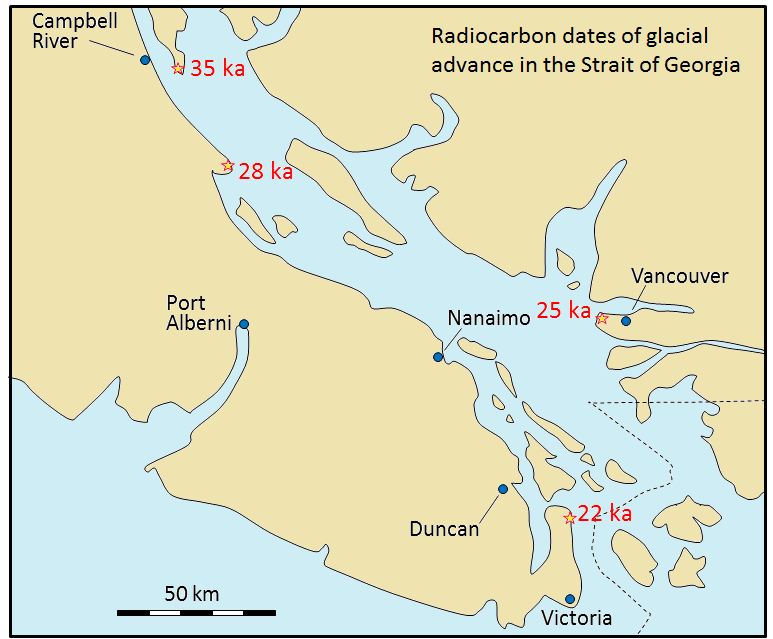
Exercise: Radiometric Dating with Potassium-Argon

Assume that a feldspar crystal from the granite shown in Figure 19.19 was analyzed for ⁴⁰K and ⁴⁰Ar. The proportion of ⁴⁰K remaining is 0.91. Using the decay curve shown on this graph, estimate the age of the rock. An example is provided (in blue) for a ⁴⁰K proportion of 0.95, which is equivalent to an age of approximately 96 Ma. This is determined by drawing a horizontal line from 0.95 to the decay curve line, and then a vertical line from there to the time axis.

References

Clague, J. (1976). Quadra Sand and its relation to late Wisconsin glaciation of southeast British Columbia. Canadian Journal of Earth Sciences, 13, 803-815.