10.6 Metamorphic Hydrothermal Processes and Metasomatism
The heat from a body of magma in the upper crust can create a very dynamic situation with geologically interesting and economically important implications. In the simplest cases, water does not play a big role, and the main process is heat transfer from the pluton to the surrounding rock, creating a zone of contact metamorphism (Figure 10.41a). In many cases, however, water is released from the magma body as crystallization takes place, and this water is dispersed along fractures in the surrounding rock (Figure 10.41b). The water released from a magma chamber is typically rich in dissolved minerals. As this water cools, it interacts with the surrounding rocks, changing both the chemistry of the water and the chemistry of the rocks. This can cause minerals to precipitate from the water. Minerals can also precipitate if the water boils because of a drop in pressure. The precipitated minerals form veins within fractures in the surrounding rock. Quartz veins are commonly formed in this situation, and can include other minerals such as pyrite, hematite, calcite, and even silver and gold.
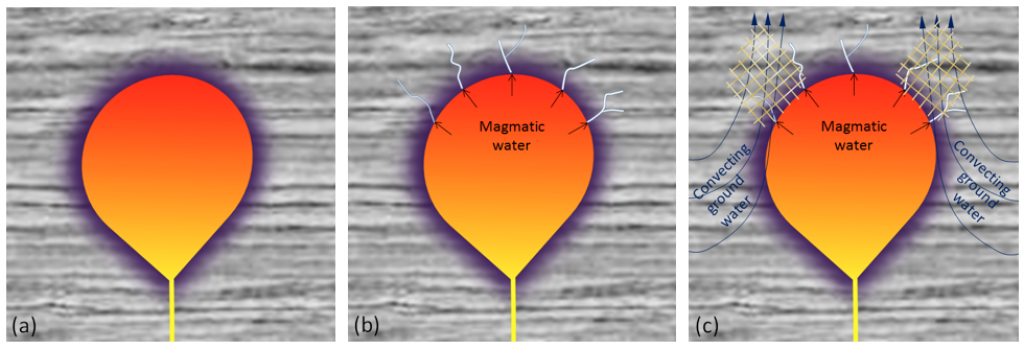
Heat from the magma body will cause surrounding groundwater to expand and then rise toward the surface. In some cases, this may initiate a convection system where groundwater circulates past the pluton. Such a system could operate for thousands of years, resulting in the circulation of millions of tonnes of groundwater from the surrounding region past the pluton.
Hot water circulating through the rocks and interacting chemically with them can lead to significant changes in the mineralogy of the rock, including alteration of feldspars to clays, and deposition of quartz, calcite, and other minerals in fractures and other open spaces (Figure 10.42). Chemical change in rocks due to interaction with hot water is called hydrothermal alteration.

Metamorphic reactions involve the release of fluids as minerals change, and chemical reactions with locally-derived fluids. However, if a large amount of externally-derived fluid—such that supplied by magma—is flushed through the system at the high pressures and temperatures characteristic of metamorphism, it can substantially alter the chemical composition of the rock. This type of hydrothermal alteration is called metasomatism.
A special type of metasomatism takes place where a hot pluton intrudes into carbonate rock such as limestone. Magmatic fluids rich in silica, calcium, magnesium, iron, and other elements can dramatically change the chemistry of the limestone, forming minerals that would not normally exist in either the igneous rock or limestone. A rock called skarn results, containing minerals such as garnet, epidote, magnetite, and pyroxene, among others (Figure 10.43).

Exercise: Contact Metamorphism and Metasomatism
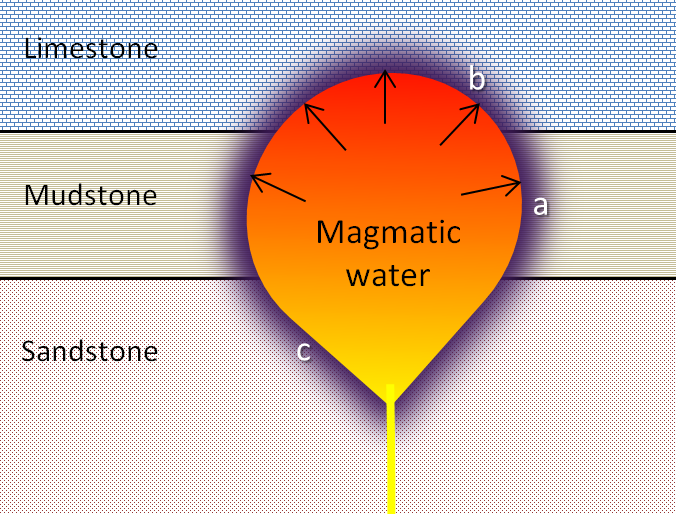
A pluton that has intruded into a series of sedimentary rocks, including sandstone, mudstone, and limestone (Figure 10.44). What types of metamorphic rocks would you expect to see at locations a, b, and c?