10 Measuring and Modeling Earth

Earth is Earth-shaped; it is also Earth-sized. For geomatics, accurate estimates of Earth’s size and shape are important, particularly when mapping large areas. We can generally agree (and most people will posit) that Earth is round (like a ball, not a disc). Scientists (mostly geophysicists) have used many methods to measure Earth’s size and shape. In the 3rd Century BCE, Eratosthenes (a librarian! like my Dad) used measurements at two locations separated by 805 km, along with arithmetic and geometry to estimate Earth’s circumference to be between 40,250 km and 45,900 km. From that time forward estimates have become increasingly accurate.  The first estimate of Earth’s size (such as Eratosthenes’) assumed Earth was spherical.

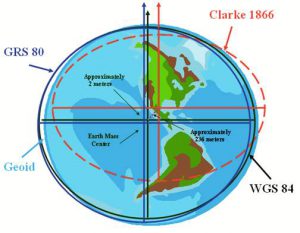
A sphere is a three dimensional shape with a single radius (distance from the edge to centre is the same everywhere). Modern models for mapping and most geomatics applications assume an oblate ellipsoid. An ellipsoid is a three dimensional shape specified by two radii, one longer than the other and orthogonal to each other (meet at a right angle at the centre of the shape). That means that an ellipsoid is longer in one dimension (it’s either “taller” than it is “wide,” or “wider”). Earth is bigger around the equator than when measured around the poles (from north to south). The orientation of its shape is defined by the term oblate. The internet (google) defines oblate as: “flattened at the poles.” if an ellipsoid is “taller” that it is “wide,” it is called prolate. Earth is oblate. BUT, Earth is covered in water, mountains, rivers, valleys, lakes, etc., it’s topographically more complicated than an ellispoid. Any model for Earth’s size and shape simplifies that complexity, doing so accurately is important. Any estimate of Earth’s size and shape is called a geodetic datum.