11 Frames of Reference and Coordinate Systems
Introduction
In order to place things in space (such as a location on Earth) a frame of reference is required. A frame of reference offers the spatial extent and reference information for all that will be placed, or can be placed, on Earth. If we want to place locations on Earth, we need a frame of reference that covers Earth’s full extent (all of it). The internet (google) defines a frame of reference as “a system of geometric axes in relation to which measurements of size, position, or motion can be made.” For geographic information, we need “axes” that will allow us to place and measure things on Earth. This is a lot easier if we assume that Earth is an easily defined shape (previous chapter), so we almost always use an oblate ellipsoid geodetic datum. Remember that this is a three dimensional roundish shape defined by two radii (one polar and one equatorial).
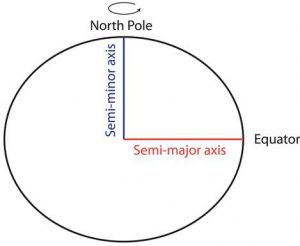
Once we have the shape and size, we establish units and origin. All frames of reference have an origin: the 0, 0 location from which measurement begins. Frames of reference also require a unit of measure; these units of measure are Cartesian (distance measurements along a line away from an origin) or Polar (rotation measurements, such as degrees, around an axis, combined with a distance measure away from the origin). In the section below, the units and origins for four different types of spaces will be presented and are defined by their shape (planar (flat, square, grid, etc.) or polar (round)) and dimensionality (two or three dimensional). As stated already planar coordinate systems use distances away from the origin while polar coordinate systems use degrees of rotation away from the baseline around the origin for at least one of the two units.
On Earth, Latitude and Longitude represent a graticule of intersecting lines that serve as a universally accepted frame of reference. The origin is the equator (0 latitude) and the Prime Meridian (0 longitude) with 90 degrees of rotation north or south from the equator to the respective poles and 180 degrees of rotation east or west from the prime meridian. Latitude and Longitude are units in a three dimensional polar coordinate system.
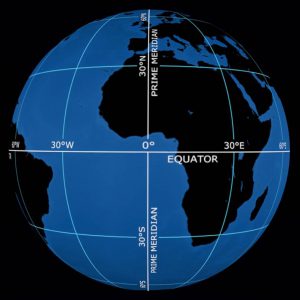
Non-Earth Based Coordinate Systems
There are four classes of coordinate systems relevant to geomatics, they are defined by their dimensionality (two-dimensional and three-dimensional) and the units of measurement (somewhat related to the shape of the space: round or orthogonal): distances or angles. Orthogonal means the space is composed of right angles. The orthogonal frames of reference (coordinate systems) will be referred to as Cartesian. Cartesian means the frame of reference is composed of baselines (axes) that intersect at right angles. The intersection point is the frame’s origin (0, 0) from which locations are specified by a length (or distance) along two axes. These two axes are often referred to as X and Y. The other set of coordinate systems are called Polar and use an angle of rotation around the origin as at least one of the coordinates. (see figures below)
Two Dimensional Coordinate Systems
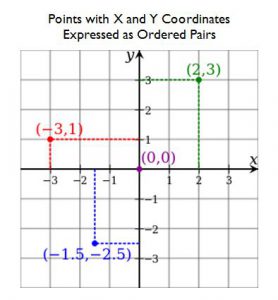
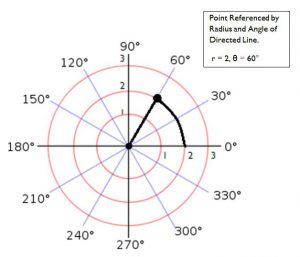
Two dimensional coordinate systems are also referred to as planar and indicate location on a flat space (or a representation of space). If the coordinate system is Cartesian, the two coordinates indicate distances along one of two axes away from from the origin. If the coordinate system is Polar the pair of coordinates indicate a distance along on an axis and a degree of rotation away from that axis around the origin.
Cartesian:
Polar:
Three Dimensional Coordinate Systems
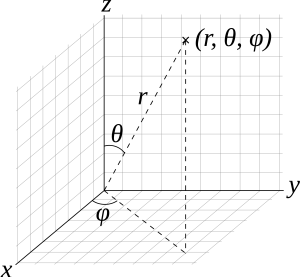
Three dimensional coordinate systems indicate position in a volumetric space. If the coordinate system is Cartesian the three coordinates indicate distances along one of three axes away from the origin. If the coordinate system is Polar the three coordinates indicate a distance along an axis and two degrees of rotation away from that axis around the origin, each orthogonal to the other.
Cartesian:
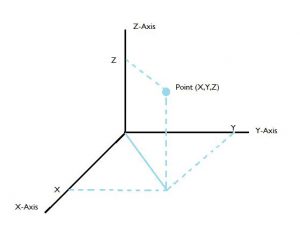
Polar:
elipsoid, sphere, oblate, and prolate ellipsoids

