16 Data Models: Representing Reality as Simply as Possible
Raster Data Model
The raster data model is widely used in applications ranging far beyond geographic information systems (GISs). Most likely, you are already very familiar with this data model if you have any experience with digital photographs. The ubiquitous JPEG, BMP, and TIFF file formats (among others) are based on the raster data model. Take a moment to view your favourite digital image. If you zoom deeply into the image, you will notice that it is composed of an array of tiny square pixels (or picture elements). Each of these uniquely colored pixels, when viewed as a whole, combines to form a coherent image (fig. 1).
Figure 1 Digital Picture with Zoomed Inset Showing Pixilation of Raster Image

Furthermore, all liquid crystal display (LCD) computer monitors are based on raster technology as they are composed of a set number of rows and columns of pixels. Notably, the foundation of this technology predates computers and digital cameras by nearly a century. The neoimpressionist artist, Georges Seurat, developed a painting technique referred to as “pointillism” in the 1880s, which similarly relies on the amassing of small, monochromatic “dots” of ink that combine to form a larger image (Fig. 2). If you are as generous as the author, you may indeed think of your raster dataset creations as sublime works of art.
Figure 2 Pointillist Artwork

The raster data model consists of rows and columns of equally sized pixels interconnected to form a planar surface. These pixels are used as building blocks for creating points, lines, areas, networks, and surfaces . Although pixels may be triangles, hexagons, or even octagons, square pixels represent the simplest geometric form with which to work. Accordingly, the vast majority of available raster GIS data are built on the square pixel (fig. 3). These squares are typically reformed into rectangles of various dimensions if the data model is transformed from one projection to another (e.g., from State Plane coordinates to UTM [Universal Transverse Mercator] coordinates).
Figure 3 Common Raster Graphics Used in GIS Applications: Aerial Photograph (left) and USGS DEM (right)

Source: Data available from U.S. Geological Survey, Earth Resources Observation and Science (EROS) Center, Sioux Falls, SD.
Because of the reliance on a uniform series of square pixels, the raster data model is referred to as a grid-based system. Typically, a single data value will be assigned to each grid locale. Each cell in a raster carries a single value, which represents the characteristic of the spatial phenomenon at a location denoted by its row and column. The data type for that cell value can be either integer (whole number) or floating-point (decimals). Alternatively, the raster graphic can reference a database management system wherein open-ended attribute tables can be used to associate multiple data values to each pixel. The advance of computer technology has made this second methodology increasingly feasible as large datasets are no longer constrained by computer storage issues as they were previously.
The raster model will average all values within a given pixel to yield a single value. Therefore, the more area covered per pixel, the less accurate the associated data values. The area covered by each pixel determines the spatial resolution of the raster model from which it is derived. Specifically, resolution is determined by measuring one side of the square pixel. A raster model with pixels representing 10 m by 10 m (or 100 square meters) in the real world would be said to have a spatial resolution of 10 m; a raster model with pixels measuring 1 km by 1 km (1 square kilometer) in the real world would be said to have a spatial resolution of 1 km; and so forth.
Care must be taken when determining the resolution of a raster because using an overly coarse pixel resolution will cause a loss of information, whereas using overly fine pixel resolution will result in significant increases in file size and computer processing requirements during display and/or analysis. An effective pixel resolution will take both the map scale and the minimum mapping unit of the other GIS data into consideration. In the case of raster graphics with coarse spatial resolution, the data values associated with specific locations are not necessarily explicit in the raster data model. For example, if the location of telephone poles were mapped on a coarse raster graphic, it would be clear that the entire cell would not be filled by the pole. Rather, the pole would be assumed to be located somewhere within that cell (typically at the center).
Imagery employing the raster data model must exhibit several properties. First, each pixel must hold at least one value, even if that data value is zero. Furthermore, if no data are present for a given pixel, a data value placeholder must be assigned to this grid cell. Often, an arbitrary, readily identifiable value (e.g., −9999) will be assigned to pixels for which there is no data value. Second, a cell can hold any alphanumeric index that represents an attribute. In the case of quantitative datasets, attribute assignation is fairly straightforward. For example, if a raster image denotes elevation, the data values for each pixel would be some indication of elevation, usually in feet or meters. In the case of qualitative datasets, data values are indices that necessarily refer to some predetermined translational rule. In the case of a land-use/land-cover raster graphic, the following rule may be applied: 1 = grassland, 2 = agricultural, 3 = disturbed, and so forth (fig. 4). The third property of the raster data model is that points and lines “move” to the centre of the cell. As one might expect, if a 1 km resolution raster image contains a river or stream, the location of the actual waterway within the “river” pixel will be unclear. Therefore, there is a general assumption that all zero-dimensional (point) and one-dimensional (line) features will be located toward the centre of the cell. As a corollary, the minimum width for any line feature must necessarily be one cell regardless of the actual width of the feature. If it is not, the feature will not be represented in the image and will therefore be assumed to be absent.
Figure 4 Land-Use/Land-Cover Raster Image

Source: Data available from U.S. Geological Survey, Earth Resources Observation and Science (EROS) Center, Sioux Falls, SD.
Several methods exist for encoding raster data from scratch. Three of these models are as follows:
- Cell-by-cell raster encoding. This minimally intensive method encodes a raster by creating records for each cell value by row and column (fig. 5). This method could be thought of as a large spreadsheet wherein each cell of the spreadsheet represents a pixel in the raster image. This method is also referred to as “exhaustive enumeration.”
- Run-length raster encoding. This method encodes cell values in runs of similarly valued pixels and can result in a highly compressed image file (fig. 6). The run-length encoding method is useful in situations where large groups of neighbouring pixels have similar values (e.g., discrete datasets such as land use/land cover or habitat suitability) and is less useful where neighbouring pixel values vary widely (e.g., continuous datasets such as elevation or sea-surface temperatures).
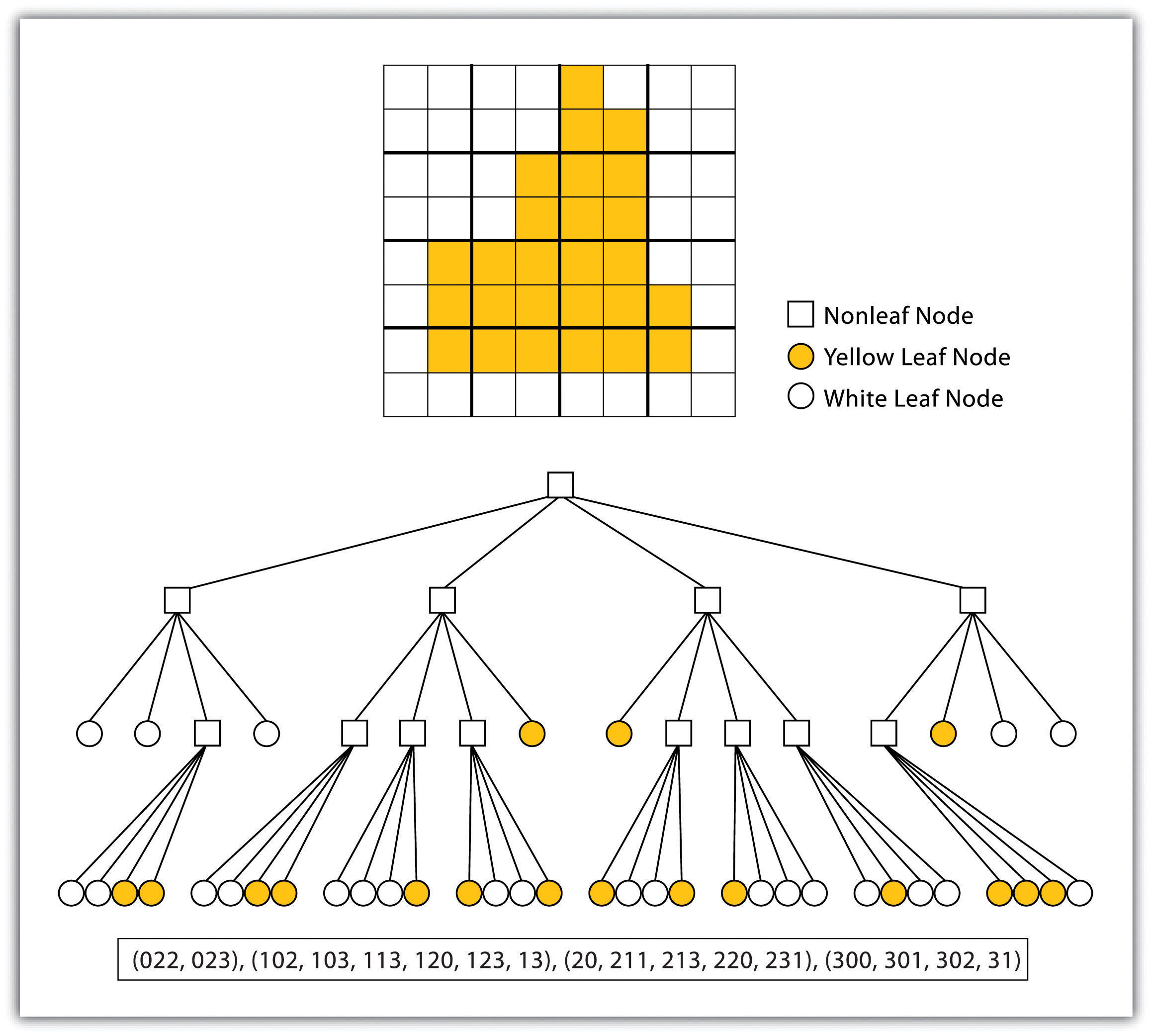
- Quad-tree raster encoding. This method divides a raster into a hierarchy of quadrants that are subdivided based on similarly valued pixels (fig. 7). The division of the raster stops when a quadrant is made entirely from cells of the same value. A quadrant that cannot be subdivided is called a “leaf node.”
Figure 5 Cell-by-Cell Encoding of Raster Data
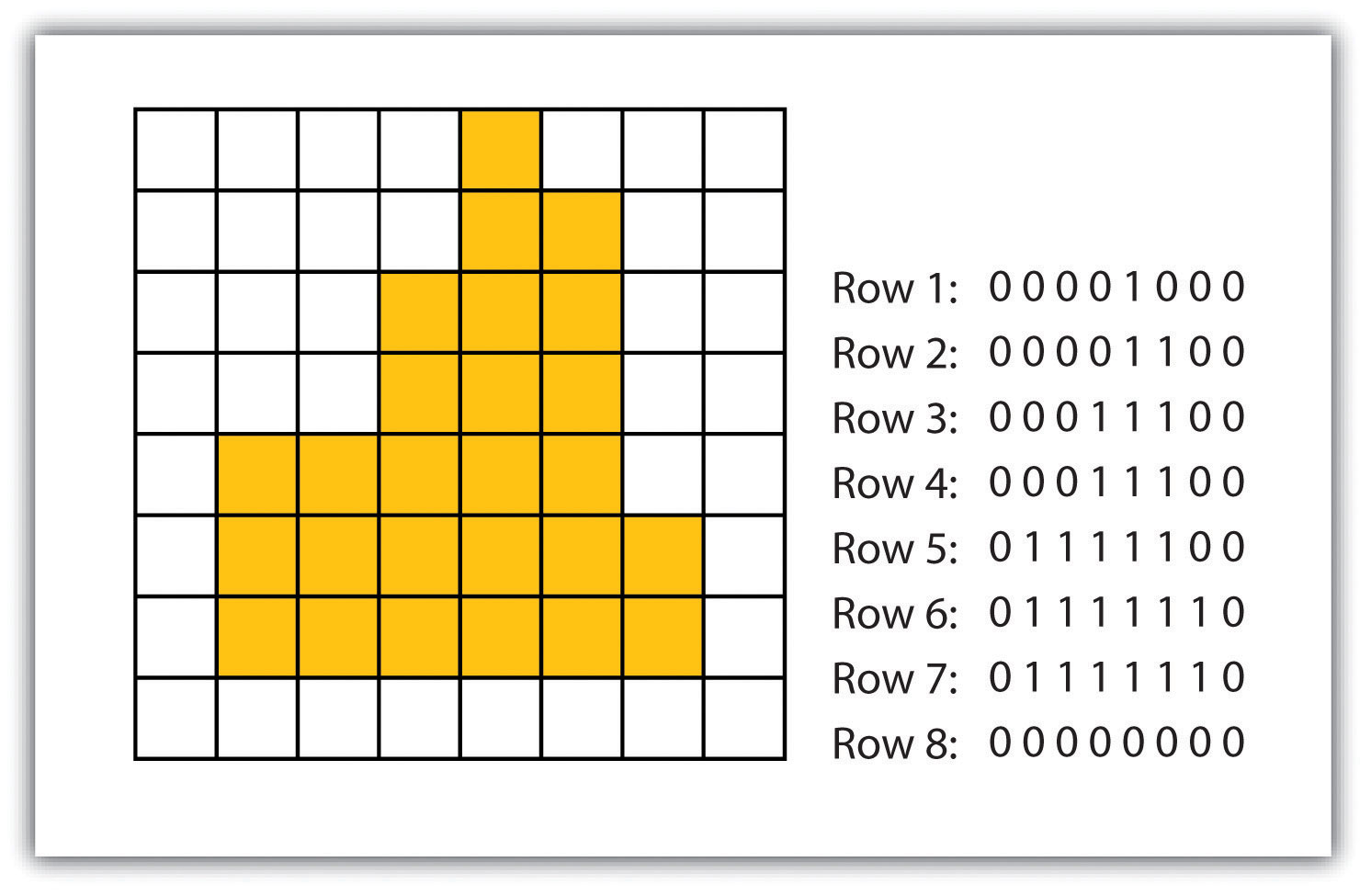
Figure 6 Run-Length Encoding of Raster Data
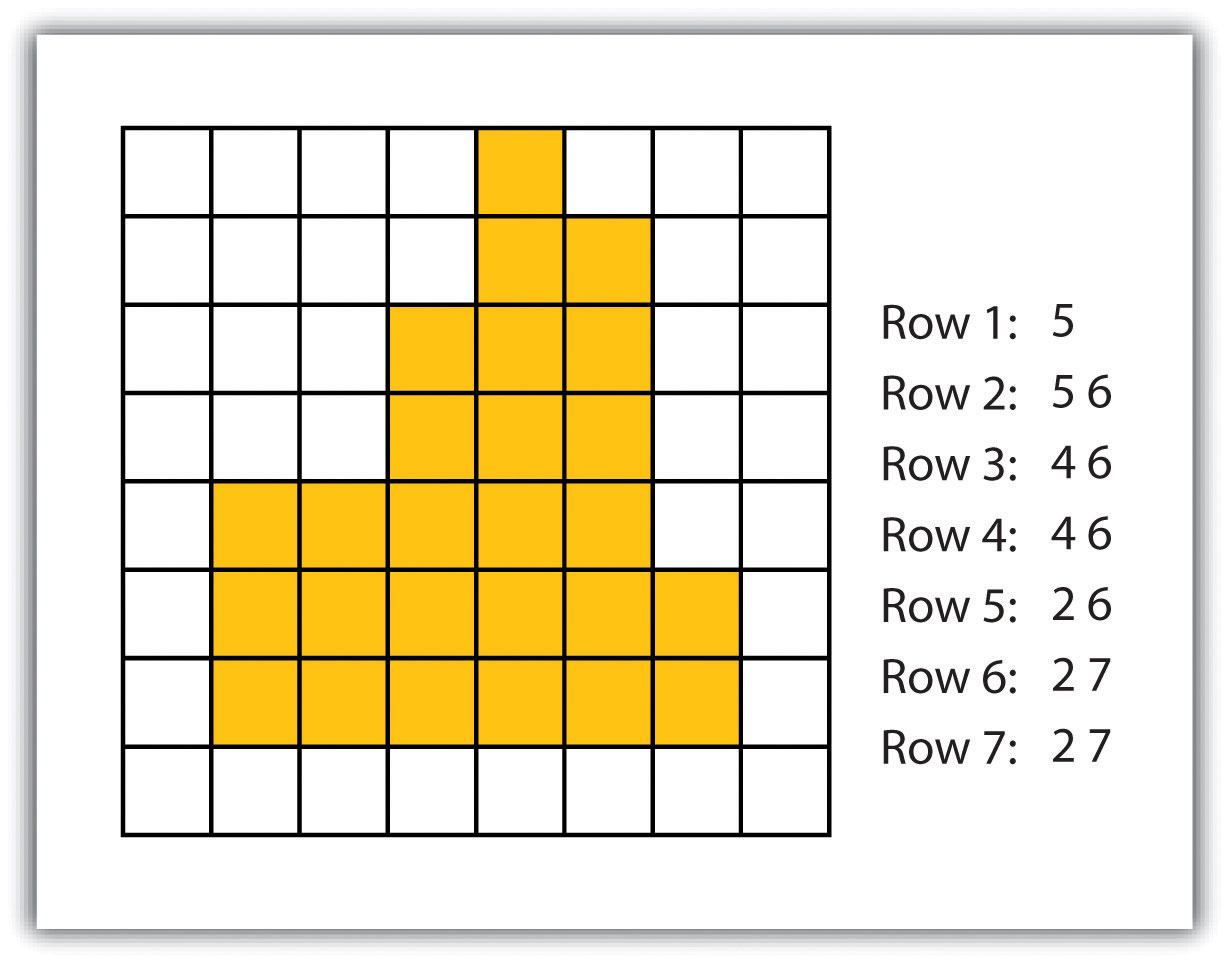
Figure 7 Quad-Tree Encoding of Raster Data
Advantages/Disadvantages of the Raster Model
The use of a raster data model confers many advantages. First, the technology required to create raster graphics is inexpensive and ubiquitous. Nearly everyone currently owns some sort of raster image generator, namely a digital camera, and few cellular phones are sold today that don’t include such functionality. Similarly, a plethora of satellites are constantly beaming up-to-the-minute raster graphics to scientific facilities across the globe. These graphics are often posted online for private and/or public use, occasionally at no cost to the user.
Additional advantages of raster graphics are the relative simplicity of the underlying data structure. Each grid location represented in the raster image correlates to a single value (or series of values if attributes tables are included). This simple data structure may also help explain why it is relatively easy to perform overlay analyses on raster data (for more on overlay analyses, see GIS Analysis chapter ). This simplicity also lends itself to easy interpretation and maintenance of the graphics, relative to its vector counterpart.
Despite the advantages, there are also several disadvantages to using the raster data model. The first disadvantage is that raster files are typically very large. Particularly in the case of raster images built from the cell-by-cell encoding methodology, the sheer number of values stored for a given dataset result in potentially enormous files. Any raster file that covers a large area and has somewhat finely resolved pixels will quickly reach hundreds of megabytes in size or more. These large files are only getting larger as the quantity and quality of raster datasets continues to keep pace with quantity and quality of computer resources and raster data collectors (e.g., digital cameras, satellites).
A second disadvantage of the raster model is that the output images are less “pretty” than their vector counterparts. This is particularly noticeable when the raster images are enlarged or zoomed fig. 4.1). Depending on how far one zooms into a raster image, the details and coherence of that image will quickly be lost amid a pixilated sea of seemingly randomly coloured grid cells.
The geometric transformations that arise during map reprojection efforts can cause problems for raster graphics and represent a third disadvantage to using the raster data model. These alterations will result in the perfect square pixels of the input layer taking on some alternate rhomboidal dimensions. However, the problem is larger than a simple reformation of the square pixel. Indeed, the reprojection of a raster image dataset from one projection to another brings change to pixel values that may, in turn, significantly alter the output information (Seong 2003).Seong, J. C. 2003. “Modeling the Accuracy of Image Data Reprojection.” International Journal of Remote Sensing 24 (11): 2309–21.
The final disadvantage of using the raster data model is that it is not suitable for some types of spatial analyses. For example, difficulties arise when attempting to overlay and analyze multiple raster graphics produced at differing scales and pixel resolutions. Combining information from a raster image with 10 m spatial resolution with a raster image with 1 km spatial resolution will most likely produce nonsensical output information as the scales of analysis are far too disparate to result in meaningful and/or interpretable conclusions. In addition, some network and spatial analyses (i.e., determining directionality or geocoding) can be problematic to perform on raster data.
Vector Data Model
In contrast to the raster data model is the vector data model. In this model, space is not quantized into discrete grid cells like the raster model. Vector data models use points and their associated X, Y coordinate pairs to represent the vertices of spatial features, much as if they were being drawn on a map by hand (Aronoff 1989).Aronoff, S. 1989. Geographic Information Systems: A Management Perspective. Ottawa, Canada: WDL Publications. The data attributes of these features are then stored in a separate database management system. The spatial information and the attribute information for these models are linked via a simple identification number that is given to each feature in a map.
Three fundamental vector types exist in geographic information systems (GISs): points, lines, and polygons (fig. 8). Points are zero-dimensional objects that contain only a single coordinate pair. Points are typically used to model singular, discrete features such as buildings, wells, power poles, sample locations, and so forth. Points have only the property of location. Other types of point features include the node and the vertex. Specifically, a point is a stand-alone feature, while a node is a topological junction representing a common X, Y coordinate pair between intersecting lines and/or polygons. Vertices are defined as each bend along a line or polygon feature that is not the intersection of lines or polygons.
Figure 8 Points, Lines, and Polygons
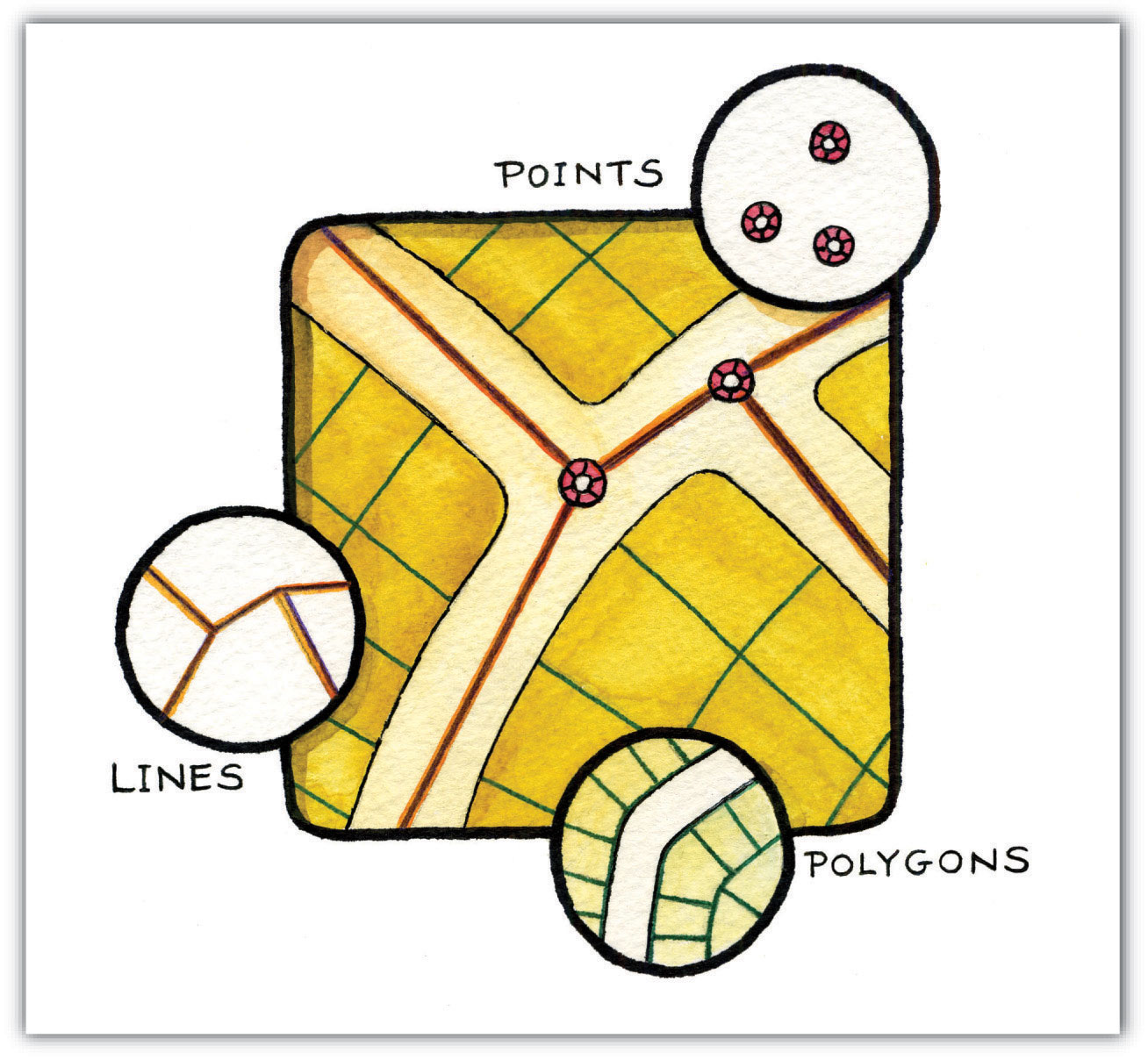
Points can be spatially linked to form more complex features. Lines are one-dimensional features composed of multiple, explicitly connected points. Lines are used to represent linear features such as roads, streams, faults, boundaries, and so forth. Lines have the property of length. Lines that directly connect two nodes are sometimes referred to as chains, edges, segments, or arcs.
Polygons are two-dimensional features created by multiple lines that loop back to create a “closed” feature. In the case of polygons, the first coordinate pair (point) on the first line segment is the same as the last coordinate pair on the last line segment. Polygons are used to represent features such as city boundaries, geologic formations, lakes, soil associations, vegetation communities, and so forth. Polygons have the properties of area and perimeter. Polygons are also called areas.
Vector Data Models Structures
Vector data models can be structured many different ways. We will examine two of the more common data structures here. The simplest vector data structure is called the spaghetti data model(Dangermond 1982).Dangermond, J. 1982. “A Classification of Software Components Commonly Used in Geographic Information Systems.” In Proceedings of the U.S.-Australia Workshop on the Design and Implementation of Computer-Based Geographic Information Systems, 70–91. Honolulu, HI. In the spaghetti model, each point, line, and/or polygon feature is represented as a string of X, Y coordinate pairs (or as a single X, Y coordinate pair in the case of a vector image with a single point) with no inherent structure (fig. 9). One could envision each line in this model to be a single strand of spaghetti that is formed into complex shapes by the addition of more and more strands of spaghetti. It is notable that in this model, any polygons that lie adjacent to each other must be made up of their own lines, or stands of spaghetti. In other words, each polygon must be uniquely defined by its own set of X, Y coordinate pairs, even if the adjacent polygons share the exact same boundary information. This creates some redundancies within the data model and therefore reduces efficiency.
Figure 9 Spaghetti Data Model

Despite the location designations associated with each line, or strand of spaghetti, spatial relationships are not explicitly encoded within the spaghetti model; rather, they are implied by their location. This results in a lack of topological information, which is problematic if the user attempts to make measurements or analysis. The computational requirements, therefore, are very steep if any advanced analytical techniques are employed on vector files structured thusly. Nevertheless, the simple structure of the spaghetti data model allows for efficient reproduction of maps and graphics as this topological information is unnecessary for plotting and printing.
In contrast to the spaghetti data model, the topological data model is characterized by the inclusion of topological information within the dataset, as the name implies. Topology is a set of rules that model the relationships between neighboring points, lines, and polygons and determines how they share geometry. These rules support cartographic transformations and are unchanged by those transformations. For example, consider two adjacent polygons. In the spaghetti model, the shared boundary of two neighboring polygons is defined as two separate, identical lines. The inclusion of topology into the data model allows for a single line to represent this shared boundary with an explicit reference to denote which side of the line belongs with which polygon. Topology is also concerned with preserving spatial properties when the forms are bent, stretched, or placed under similar geometric transformations, which allows for more efficient projection and reprojection of map files.
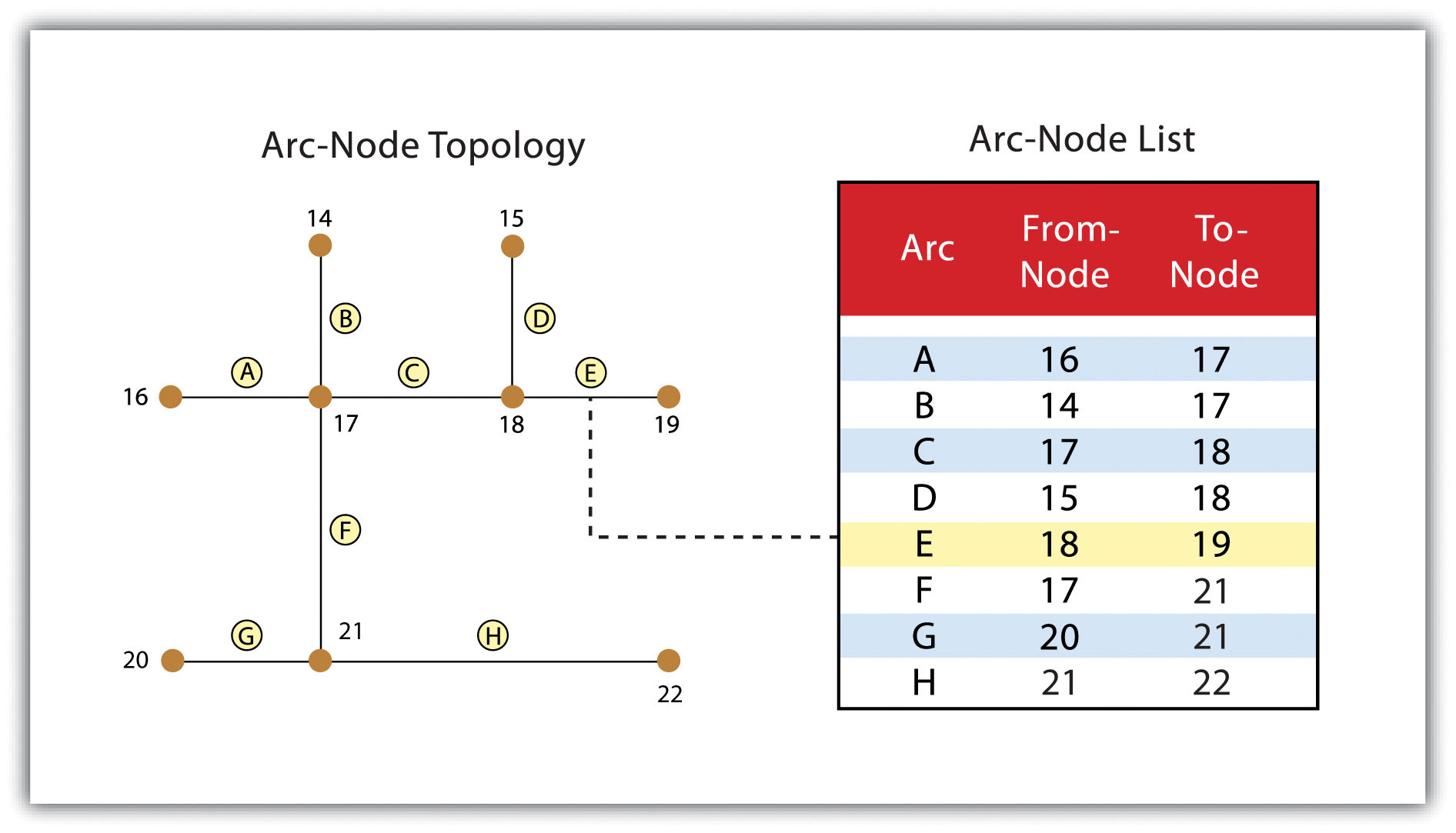
Three basic topological precepts that are necessary to understand the topological data model are outlined here. First, connectivity describes the arc-node topology for the feature dataset. As discussed previously, nodes are more than simple points. In the topological data model, nodes are the intersection points where two or more arcs meet. In the case of arc-node topology, arcs have both a from-node (i.e., starting node) indicating where the arc begins and a to-node (i.e., ending node) indicating where the arc ends (fig 10). In addition, between each node pair is a line segment, sometimes called a link, which has its own identification number and references both its from-node and to-node. In fig. 10, arcs 1, 2, and 3 all intersect because they share node 11. Therefore, the computer can determine that it is possible to move along arc 1 and turn onto arc 3, while it is not possible to move from arc 1 to arc 5, as they do not share a common node.
Figure 10 Arc-Node Topology
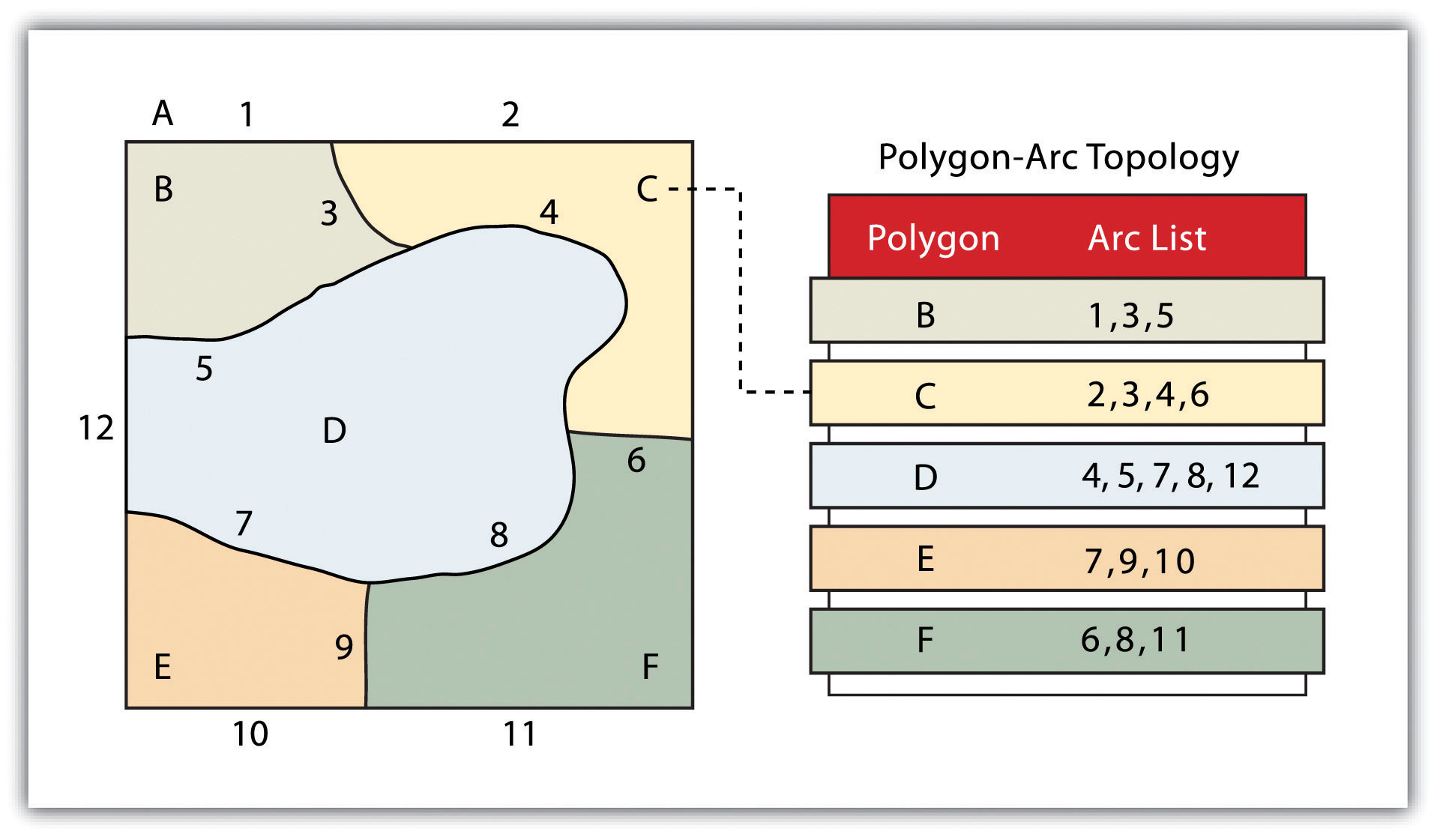
The second basic topological precept is area definition. Area definition states that an arc that connects to surround an area defines a polygon, also called polygon-arc topology. In the case of polygon-arc topology, arcs are used to construct polygons, and each arc is stored only once (fig. 11). This results in a reduction in the amount of data stored and ensures that adjacent polygon boundaries do not overlap. In the fig. 11, the polygon-arc topology makes it clear that polygon F is made up of arcs 8, 9, and 10.
Figure 11 Polygon-Arc Topology
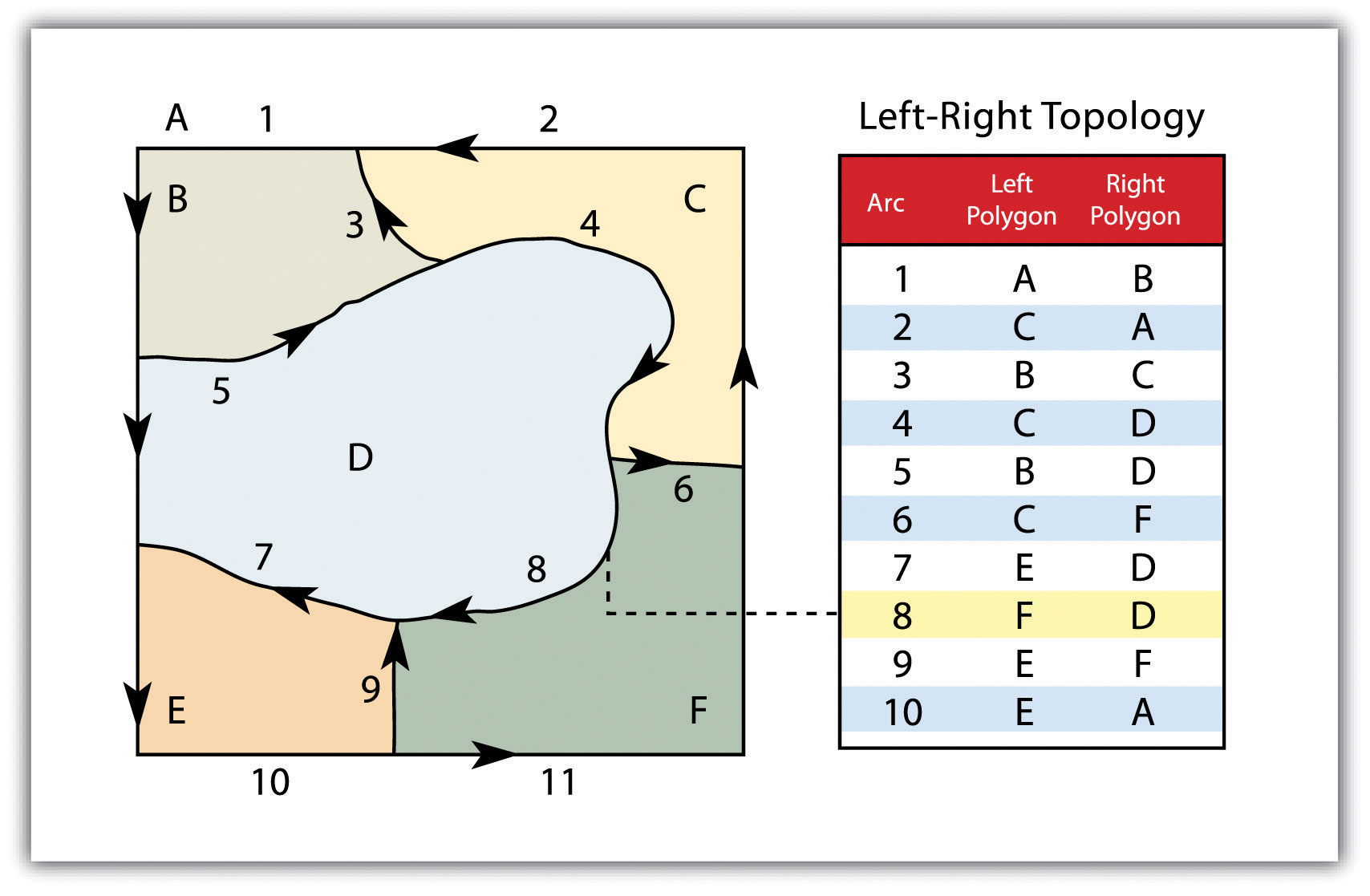
Contiguity, the third topological precept, is based on the concept that polygons that share a boundary are deemed adjacent. Specifically, polygon topology requires that all arcs in a polygon have a direction (a from-node and a to-node), which allows adjacency information to be determined (fig. 12). Polygons that share an arc are deemed adjacent, or contiguous, and therefore the “left” and “right” side of each arc can be defined. This left and right polygon information is stored explicitly within the attribute information of the topological data model. The “universe polygon” is an essential component of polygon topology that represents the external area located outside of the study area. Fig. 12 shows that arc 6 is bound on the left by polygon B and to the right by polygon C. Polygon A, the universe polygon, is to the left of arcs 1, 2, and 3.
Figure 12 Polygon Topology
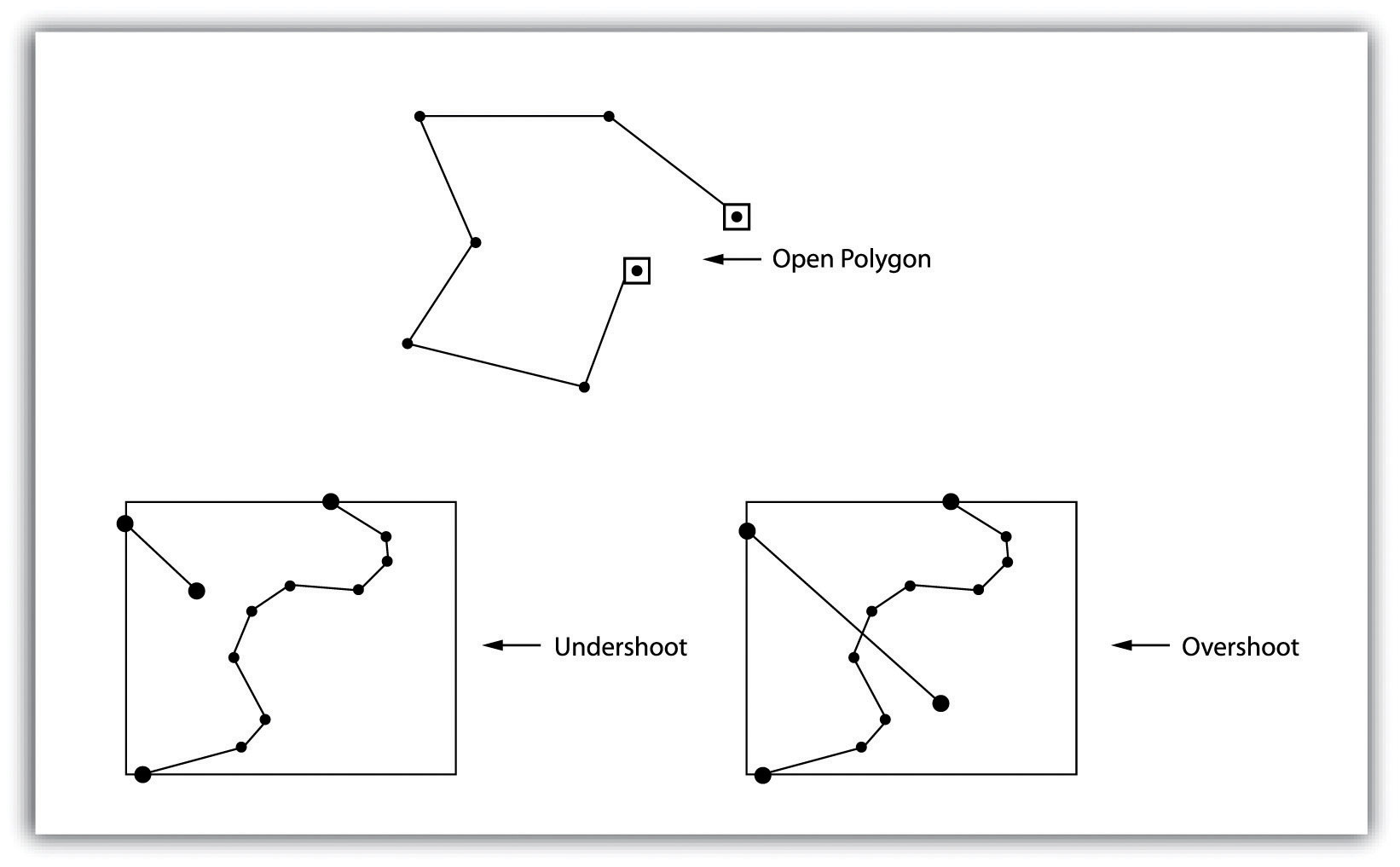
Topology allows the computer to rapidly determine and analyze the spatial relationships of all its included features. It supports cartographic transformation of the spatial information from one coordinate system to another. The coordinate systems can been based on a map projection or the geodetic datum. In addition, topological information is important because it allows for efficient error detection within a vector dataset. In the case of polygon features, open or unclosed polygons, which occur when an arc does not completely loop back upon itself, and unlabeled polygons, which occur when an area does not contain any attribute information, violate polygon-arc topology rules. Another topological error found with polygon features is the sliver. Slivers occur when the shared boundary of two polygons do not meet exactly (fig. 13).
In the case of line features, topological errors occur when two lines do not meet perfectly at a node. This error is called an “undershoot” when the lines do not extend far enough to meet each other and an “overshoot” when the line extends beyond the feature it should connect to (fig. 13). The result of overshoots and undershoots is a “dangling node” at the end of the line. Dangling nodes aren’t always an error, however, as they occur in the case of dead-end streets on a road map.
Figure 13 Common Topological Errors
Many types of spatial analysis require the degree of organization offered by topologically explicit data models. In particular, network analysis (e.g., finding the best route from one location to another) and measurement (e.g., finding the length of a river segment) relies heavily on the concept of to- and from-nodes and uses this information, along with attribute information, to calculate distances, shortest routes, quickest routes, and so forth. Topology also allows for sophisticated neighborhood analysis such as determining adjacency, clustering, nearest neighbors, and so forth.
Now that the basics of the concepts of topology have been outlined, we can begin to better understand the topological data model. In this model, the node acts as more than just a simple point along a line or polygon. The node represents the point of intersection for two or more arcs. Arcs may or may not be looped into polygons. Regardless, all nodes, arcs, and polygons are individually numbered. This numbering allows for quick and easy reference within the data model.
Advantages/Disadvantages of the Vector Model
In comparison with the raster data model, vector data models tend to be better representations of reality due to the accuracy and precision of points, lines, and polygons over the regularly spaced grid cells of the raster model. This results in vector data tending to be more aesthetically pleasing than raster data.
Vector data also provides an increased ability to alter the scale of observation and analysis. As each coordinate pair associated with a point, line, and polygon represents an infinitesimally exact location (albeit limited by the number of significant digits and/or data acquisition methodologies), zooming deep into a vector image does not change the view of a vector graphic in the way that it does a raster graphic (see fig. 1).
Vector data tend to be more compact in data structure, so file sizes are typically much smaller than their raster counterparts. Although the ability of modern computers has minimized the importance of maintaining small file sizes, vector data often require a fraction the computer storage space when compared to raster data.
The final advantage of vector data is that topology is inherent in the vector model. This topological information results in simplified spatial analysis (e.g., error detection, network analysis, proximity analysis, and spatial transformation) when using a vector model.
Alternatively, there are two primary disadvantages of the vector data model. First, the data structure tends to be much more complex than the simple raster data model. As the location of each vertex must be stored explicitly in the model, there are no shortcuts for storing data like there are for raster models (e.g., the run-length and quad-tree encoding methodologies).
Second, the implementation of spatial analysis can also be relatively complicated due to minor differences in accuracy and precision between the input datasets. Similarly, the algorithms for manipulating and analyzing vector data are complex and can lead to intensive processing requirements, particularly when dealing with large datasets.

