12 Cartesian/Projected Coordinate Systems, UTM

Introduction

When we translate the previous topic, coordinate systems of different types and dimensions (polar/cartesian and 2D/3D), to Earth, we need to integrate what we know about Earth’s size and shape. As summarized in this section’s first chapter, Earth is Earth-sized and shaped, but can be simplified to an oblate ellipsoid. An oblate ellipsoid is a 3-dimensional round shape, making its native coordinate system a Polar 3D system.

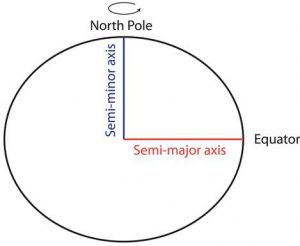
The origin for this system is the centre of the ellipsoid, with the distance unit representing the distance from the origin to the surface of the ellipsoid. This means the distance to the surface changes continuously from the equator to poles. The distance to the surface from the centroid of the geodetic datum (Earth model) is the radius of Earth. For the most part we treat the surface (and corresponding value for the distance to it from the ellipsoid’s centre) as a constant.

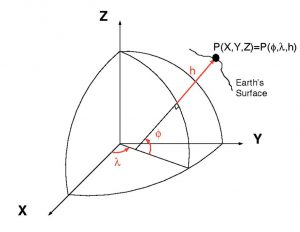
For the two remaining units, each indicating a number of degrees of rotation around the origin, we use Latitude and Longitude. The origin for these values is the intersection of the Equator and the Prime Meridian. The equator is the midpoint between the two poles. The two poles are defined as the points connected by a line perpendicular to Earth’s rotation.The Prime Meridian is an arbitrary, but negotiated, line that passes through Greenwich, England.

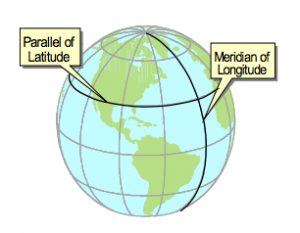
Having a coordinate system that is native to Earth’s shape (or close to it) is intuitive and efficient. In particular, once an origin is specified all locations can be expressed with just two values, Latitude and Longitude, in a common unit, degrees. The challenge is using such values in calculations of area and distance. The math is complicated, to say it simply. If we ask a question from the perspective of calculation complexity, such as “what type of coordinate system supports the most simple distance and area calculations?” The answer is 2-dimensional cartesian, such as Universal Transverse Mercator (UTM)

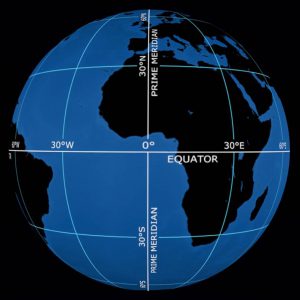
UTM

Universal Transverse Mercator (UTM) is a map projection-based global coordinate system that provides location information using pairs of Cartesian coordinates in metric units (metres). UTM offers location information in a coordinate system (2-D cartesian) that offer a simpler calculation environment than its most popular 3-D polar counterpart (Latitude and Longitude). As you have learned, Earth is a 3-D ellipsoid, making its native coordinate system 3-D polar.

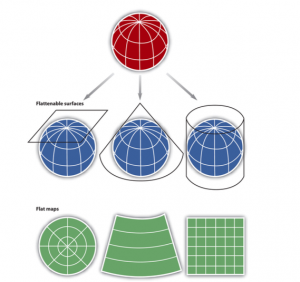
Conversions from one coordinate system to another requires a mathematical process called projection. In this textbook and the accompanying course, this process was initially introduced as a process that uses the term “projected” in a colloquial sense; the surface of Earth was projected onto a paper surface using a light source casting shadows onto a piece of paper. This simultaneously relies on the complexity of systematically converting coordinates in one system to another system. The mathematics aren’t trivial, but by initiating the process with shadows, light, and piece of paper does offer a tantalizing means to “get the idea” of what is happening.

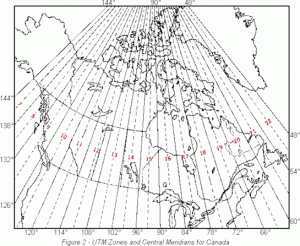
Coordinates in UTM are specified by a Zone (1-60), a hemisphere (N or S), and a Northing (in metres), and Eastings (also in metres). Let’s figure those out.

First Conversion

Actually 60 of them. As we have learned, the amount of error, or uncertainty, on a map projection increases as distance from the standard point, line, or lines increases. Close to a standard line we have less to worry about. UTM is composed of 60 separate zones, each a small sliver of Earth centred on a line of longitude. The name of the projection and its orientation is hidden in plain sight (in the name of the coordinate system). The projection is the Mercator and its orientation is transverse. In this situation transverse means rotated 90 degrees from Mercator projection’s normal orientation. The Mercator projection’s normal orientation is with the standard line at the equator. Lines of longitude run at a 90 degree angle to the equator.

BUT, why 60? As noted, increasing distance from the standard line increases error. Therefore, the UTM system uses a single projection for just a 6 degree swath of Earth. As an ellipsoid, the circumference of Earth is 360 degrees (360/6 = 60 zones!). Each zone has a name, starting with the line opposite the Prime Meridian (180 degrees, east or west), and moving east. The first zone is zone 1, the final zone is zone 60. Saskatchewan is covered by Zone 13.

Coordinates in UTM start with the zone, then the hemisphere: North (N) or South (S). Dividing the system into N and S allows the system to use the equator and its fictional, but parallel equivalent as the baselines for one of the coordinate pairs. This is elegant (it really struck me at learning it, a simple insight, but one that supports an intuitive conversion from polar to Cartesian coordinates). When observing Earth with lines of latitude and longitude depicted and making the centre of the “picture” the intersection of the equator and a line of longitude (like 105 degrees W) looks just like the intersection of two lines in a 2-D cartesian coordinate system. What we AREN’T seeing though, is that each line (0 degrees latitude and 105 degrees west) is receding away from us (the viewer) along the surface of the ellipsoid.