Chapter 9 Review

Samuel J. Ling; Jeff Sanny; William Moebs; Daryl Janzen

Chapter 9 Review

Key Terms

Ampère’s law
physical law that states that the line integral of the magnetic field around an electric current is proportional to the current

Biot-Savart law
an equation giving the magnetic field at a point produced by a current-carrying wire

diamagnetic materials
their magnetic dipoles align oppositely to an applied magnetic field; when the field is removed, the material is unmagnetized

ferromagnetic materials
contain groups of dipoles, called domains, that align with the applied magnetic field; when this field is removed, the material is still magnetized

hysteresis
property of ferromagnets that is seen when a material’s magnetic field is examined versus the applied magnetic field; a loop is created resulting from sweeping the applied field forward and reverse

magnetic domains
groups of magnetic dipoles that are all aligned in the same direction and are coupled together quantum mechanically

magnetic susceptibility
ratio of the magnetic field in the material over the applied field at that time; positive susceptibilities are either paramagnetic or ferromagnetic (aligned with the field) and negative susceptibilities are diamagnetic (aligned oppositely with the field)

paramagnetic materials
their magnetic dipoles align partially in the same direction as the applied magnetic field; when this field is removed, the material is unmagnetized

permeability of free space
$\mu_0,$ measure of the ability of a material, in this case free space, to support a magnetic field

solenoid
thin wire wound into a coil that produces a magnetic field when an electric current is passed through it

toroid
donut-shaped coil closely wound around that is one continuous wire

Key Equations

Permeability of free space	$\mu_0=4\pi\times10^{-7}~\mathrm{T}\cdot\mathrm{m/A}$
Contribution to magnetic field from a current element	$dB=\frac{\mu_0}{4\pi}\frac{Idlsin\theta}{r^2}$
Biot–Savart law	$\vec{\mathbf{B}}=\frac{\mu_0}{4\pi}\int_{\mathrm{wire}}\frac{Id\vec{\mathbf{l}}\times\hat{\mathbf{r}}}{r^2}$
Magnetic field due to a long straight wire	$B=\frac{\mu_0I}{2\pi R}$
Force between two parallel currents	$\frac{F}{l}=\frac{\mu_0I_1I_2}{2\pi r}$
Magnetic field of a current loop	$B=\frac{\mu_0I}{2R}$ (at Center of loop)
Ampère’s law	$\oint\vec{\mathbf{B}}\cdot\vec{\mathbf{dl}}=\mu_0I$
Magnetic field strength inside a solenoid	$B=\mu_0nI$
Magnetic field strength inside a toroid	$B=\frac{\mu_0NI}{2\pi r}$
Magnetic permeability	$\mu=(1+\chi)\mu_0$
Magnetic field of a solenoid filled with paramagnetic material	$B=\mu nI$

Magnetic field due to a

Summary

9.1 The Biot-Savart Law

The magnetic field created by a current-carrying wire is found by the Biot-Savart law.
The current element 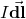$I\vec{\mathbf{dl}}$ produces a magnetic field a distance $r$ away.

9.2 Magnetic Field Due to a Thin Straight Wire

The strength of the magnetic field created by current in a long straight wire is given by 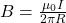$B=\frac{\mu_0I}{2\pi R}$ (long straight wire) where 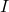$I$ is the current, 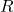$R$ is the shortest distance to the wire, and the constant 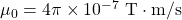$\mu_0=4\pi\times10^{-7}~\mathrm{T}\cdot\mathrm{m/s}$ is the permeability of free space.
The direction of the magnetic field created by a long straight wire is given by right-hand rule $2$ (RHR $2$ ): Point the thumb of the right hand in the direction of current, and the fingers curl in the direction of the magnetic field loops created by it.

9.3 Magnetic Force between Two Parallel Currents

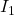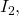The force between two parallel currents $I_1$ and $I_2,$ separated by a distance 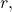$r,$ has a magnitude per unit length given by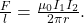 $\frac{F}{l}=\frac{\mu_0I_1I_2}{2\pi r}.$
The force is attractive if the currents are in the same direction, repulsive if they are in opposite directions.

9.4 Magnetic Field of a Current Loop

The magnetic field strength at the center of a circular loop is given by 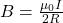$B=\frac{\mu_0I}{2R}$ (at center of loop), where 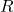$R$ is the radius of the loop. RHR-2 gives the direction of the field about the loop.

9.5 Ampère’s Law

The magnetic field created by current following any path is the sum (or integral) of the fields due to segments along the path (magnitude and direction as for a straight wire), resulting in a general relationship between current and field known as Ampère’s law.
Ampère’s law can be used to determine the magnetic field from a thin wire or thick wire by a geometrically convenient path of integration. The results are consistent with the Biot-Savart law.

9.6 Solenoids and Toroids

The magnetic field strength inside a solenoid is

$B=\mu_0nI$

(inside a solenoid)

where $n$ is the number of loops per unit length of the solenoid. The field inside is very uniform in magnitude and direction.

The magnetic field strength inside a toroid is

$B=\frac{\mu_0NI}{2\pi r}$

(within the toroid)

where $N$ is the number of windings. The field inside a toroid is not uniform and varies with the distance as $1/r.$

9.7 Magnetism in Matter

Materials are classified as paramagnetic, diamagnetic, or ferromagnetic, depending on how they behave in an applied magnetic field.
Paramagnetic materials have partial alignment of their magnetic dipoles with an applied magnetic field. This is a positive magnetic susceptibility. Only a surface current remains, creating a solenoid-like magnetic field.
Diamagnetic materials exhibit induced dipoles opposite to an applied magnetic field. This is a negative magnetic susceptibility.
Ferromagnetic materials have groups of dipoles, called domains, which align with the applied magnetic field. However, when the field is removed, the ferromagnetic material remains magnetized, unlike paramagnetic materials. This magnetization of the material versus the applied field effect is called hysteresis.

Answers to Check Your Understanding

9.1 $1.41~\mathrm{m}$

9.2 $\frac{\mu_0I}{2R}$

9.3 4 amps flowing out of the page

9.4 Both have a force per unit length of $9.23\times10^{-12}~\mathrm{N/m}$

9.5 $0.608~\mathrm{m}$

9.6 In these cases the integrals around the Ampèrian loop are very difficult because there is no symmetry, so this method would not be useful.

9.7 a. $1.00382;$ b. $1.00015$

9.8 a. $1.0\times10^{-4}~\mathrm{T};$ b. $0.60~\mathrm{T};$ c. $6.0\times10^3$

Conceptual Questions

9.1 The Biot-Savart Law

1. For calculating magnetic fields, what are the advantages and disadvantages of the Biot-Savart law?

2. Describe the magnetic field due to the current in two wires connected to the two terminals of a source of emf and twisted tightly around each other.

3. How can you decide if a wire is infinite?

4. Identical currents are carried in two circular loops; however, one loop has twice the diameter as the other loop. Compare the magnetic fields created by the loops at the center of each loop.

9.2 Magnetic Field Due to a Thin Straight Wire

5. How would you orient two long, straight, current-carrying wires so that there is no net magnetic force between them? (Hint: What orientation would lead to one wire not experiencing a magnetic field from the other?)

9.3 Magnetic Force between Two Parallel Currents

6. Compare and contrast the electric field of an infinite line of charge and the magnetic field of an infinite line of current.

7. Is $\vec{\mathbf{B}}$ constant in magnitude for points that lie on a magnetic field line?

9.4 Magnetic Field of a Current Loop

8. Is the magnetic field of a current loop uniform?

9. What happens to the length of a suspended spring when a current passes through it?

10. Two concentric circular wires with different diameters carry currents in the same direction. Describe the force on the inner wire.

9.5 Ampère’s Law

11. Is Ampère’s law valid for all closed paths? Why isn’t it normally useful for calculating a magnetic field?

9.6 Solenoids and Toroids

12. Is the magnetic field inside a toroid completely uniform? Almost uniform?

13. Explain why $\vec{\mathbf{B}}=0$ inside a long, hollow copper pipe that is carrying an electric current parallel to the axis. Is $\vec{\mathbf{B}}=0$ outside the pipe?

9.7 Magnetism in Matter

14. A diamagnetic material is brought close to a permanent magnet. What happens to the material?

15. If you cut a bar magnet into two pieces, will you end up with one magnet with an isolated north pole and another magnet with an isolated south pole? Explain your answer.

Problems

9.1 The Biot-Savart Law

16. A $10{\text -}\mathrm{A}$ current flows through the wire shown. What is the magnitude of the magnetic field due to a $0.5{\text -}\mathrm{mm}$ segment of wire as measured at (a) point A and (b) point B?

This figure shows a piece of wire. Point A is located 3 centimeters above the 0.5 mm segment of wire. Point B is located 4 centimeters to the right of point A.

17. Ten amps flow through a square loop where each side is $20~\mathrm{cm}$ in length. At each corner of the loop is a $0.01{\text -}\mathrm{cm}$ segment that connects the longer wires as shown. Calculate the magnitude of the magnetic field at the center of the loop.

A square loop is shown with rounded corners. There are no markings.

18. What is the magnetic field at P due to the current $I$ in the wire shown?

This figure shows a current loop consisting of two concentric circular arcs and two parallel radial lines. Outer arc is located at the distance b from the center; inner arc is located at the distance a from the center.

19. The accompanying figure shows a current loop consisting of two concentric circular arcs and two perpendicular radial lines. Determine the magnetic field at point P.

This figure shows a current loop consisting of two concentric circular arcs and two perpendicular radial lines. Outer arc is located at the distance b from the center; inner arc is located at the distance a from the center.

20. Find the magnetic field at the center C of the rectangular loop of wire shown in the accompanying figure.

This figure shows a rectangular current loop. The length of the short side is b; the length of the long side is a. Point C is a center of the loop.

21. Two long wires, one of which has a semicircular bend of radius $R,$ are positioned as shown in the accompanying figure. If both wires carry a current $I,$ how far apart must their parallel sections be so that the net magnetic field at P is zero? Does the current in the straight wire flow up or down?

This figure shows two parallel long wires located at a distance a from each other. One of the wires has a semicircular bend of radius R.

9.2 Magnetic Field Due to a Thin Straight Wire

22. A typical current in a lightning bolt is $10^4~\mathrum{A}.$ Estimate the magnetic field $1~\mathrm{m}$ from the bolt.

23. The magnitude of the magnetic field $50~\mathrm{cm}$ from a long, thin, straight wire is $8.0~\mu\mathrm{T}.$ What is the current through the long wire?

24. A transmission line strung $7.0~\mathrm{m}$ above the ground carries a current of $500~\mathrm{A}.$ What is the magnetic field on the ground directly below the wire? Compare your answer with the magnetic field of Earth.

25. A long, straight, horizontal wire carries a left-to-right current of $20~\mathrm{A}.$ If the wire is placed in a uniform magnetic field of magnitude $4.0\times10^{-5}~\mathrm{T}$ that is directed vertically downward, what is the resultant magnitude of the magnetic field $20~\mathrm{cm}$ above the wire? $20~\mathrm{cm}$ below the wire?

26. The two long, parallel wires shown in the accompanying figure carry currents in the same direction. If $I_1=10~\mathrm{A}$ and $I_2=20~\mathrm{A},$ what is the magnetic field at point P?

27. The accompanying figure shows two long, straight, horizontal wires that are parallel and a distance $2a$ apart. If both wires carry current $I$ in the same direction, (a) what is the magnetic field at $P_1$ ? (b) $P_2$ ?

Figure shows two long parallel wires that are distance 2a apart. Current flows through the wires in the same direction. Point P1 is located between the wires at a distance a from each. Point P2 is located at a distance 2 a outside the wires.

28. Repeat the calculations of the preceding problem with the direction of the current in the lower wire reversed.

29. Consider the area between the wires of the preceding problem. At what distance from the top wire is the net magnetic field a minimum? Assume that the currents are equal and flow in opposite directions.

9.3 Magnetic Force between Two Parallel Currents

30. Two long, straight wires are parallel and $25~\mathrm{cm}$ apart. (a) If each wire carries a current of $50~\mathrm{A}$ in the same direction, what is the magnetic force per meter exerted on each wire? (b) Does the force pull the wires together or push them apart? (c) What happens if the currents flow in opposite directions?

31. Two long, straight wires are parallel and $10~\mathrm{cm}$ apart. One carries a current of $2.0~\mathrm{A},$ the other a current of $5.0~\mathrm{A}.$ (a) If the two currents flow in opposite directions, what is the magnitude and direction of the force per unit length of one wire on the other? (b) What is the magnitude and direction of the force per unit length if the currents flow in the same direction?

32. Two long, parallel wires are hung by cords of length $5.0~\mathrm{cm},$ as shown in the accompanying figure. Each wire has a mass per unit length of $30~\mathrm{g/m},$ and they carry the same current in opposite directions. What is the current if the cords hang at $6.0^{\circ}$ with respect to the vertical?

Figure shows two parallel wires with current flowing in opposite directions that are hung by cords suspended from hooks.

33. A circuit with current $I$ has two long parallel wire sections that carry current in opposite directions. Find magnetic field at a point P near these wires that is a distance $a$ from one wire and $b$ from the other wire as shown in the figure.

Figure shows two current carrying wires. One carries current out of the page; another carries current into the page. Wires form vertices of a right triangle. Point P is the third vertex and is located at a distance b from one wire and distance a from another wire. Distance b is a leg; distance a is a hypotenuse.

34. The infinite, straight wire shown in the accompanying figure carries a current $I_1.$ The rectangular loop, whose long sides are parallel to the wire, carries a current $I_2.$ What are the magnitude and direction of the force on the rectangular loop due to the magnetic field of the wire?

Figure shows a wire that carries the current I1 and a rectangular loop with long sides that are parallel to the wire and carry a current I2. Distance between the wire and the loop is b. Length of the side of the long side of the loop is a, distance of the short side of the loop is b.

9.4 Magnetic Field of a Current Loop

35. When the current through a circular loop is $6.0~\mathrm{A},$ the magnetic field at its center is $2.0\times10^{-4}~\mathrm{T}.$ What is the radius of the loop?

36. How many turns must be wound on a flat, circular coil of radius $20~\mathrm{cm}$ in order to produce a magnetic field of magnitude $4.0\times10^{-5}~\mathrm{T}$ at the center of the coil when the current through it is $0.85~\mathrm{A}$ ?

37. A flat, circular loop has $20$ turns. The radius of the loop is $10.0~\mathrm{cm}$ and the current through the wire is $0.50~\mathrm{A}.$ Determine the magnitude of the magnetic field at the center of the loop.

38. A circular loop of radius $R$ carries a current $I.$ At what distance along the axis of the loop is the magnetic field one-half its value at the center of the loop?

39. Two flat, circular coils, each with a radius $R$ and wound with $N$ turns, are mounted along the same axis so that they are parallel a distance $d$ apart. What is the magnetic field at the midpoint of the common axis if a current $I$ flows in the same direction through each coil?

40. For the coils in the preceding problem, what is the magnetic field at the center of either coil?

9.5 Ampère’s Law

41. A current $I$ flows around the rectangular loop shown in the accompanying figure. Evaluate $\oint\vec{\mathbf{B}}\cdot\vec{\mathbf{dl}}$ for the paths $A,$ $B,$ $C,$ and $D.$

Figure shows rectangular loop carrying current I. Paths A and C intersect with the short sides of the loop. Path B intersects with the two long sides of the loop. Path D intersects both with the short and the long sides of the loop.

42. Evaluate $\oint\vec{\mathbf{B}}\cdot\vec{\mathbf{dl}}$ for each of the cases shown in the accompanying figure.

43. The coil whose lengthwise cross section is shown in the accompanying figure carries a current $I$ and has $N$ evenly spaced turns distributed along the length $l.$ Evaluate $\oint\vec{\mathbf{B}}\cdot\vec{\mathbf{dl}}$ for the paths indicated.

44. A superconducting wire of diameter $0.25~\mathrm{cm}$ carries a current of $1000~\mathrm{A}.$ What is the magnetic field just outside the wire?

45. A long, straight wire of radius $R$ carries a current $I$ that is distributed uniformly over the cross-section of the wire. At what distance from the axis of the wire is the magnitude of the magnetic field a maximum?

46. The accompanying figure shows a cross-section of a long, hollow, cylindrical conductor of inner radius $r_1=3.0~\mathrm{cm}$ and outer radius $r_2=5.0~\mathrm{cm}.$ A $50{\text -}\mathrm{A}$ current distributed uniformly over the cross-section flows into the page. Calculate the magnetic field at $r=2.0~\mathrm{cm},$ $r=4.0~\mathrm{cm},$ and $r=6.0~\mathrm{cm}.$

Figure shows a cross-section of a long, hollow, cylindrical conductor with an inner radius of three centimeters and an outer radius of five centimeters.

47. A long, solid, cylindrical conductor of radius $3.0~\mathrm{cm}$ carries a current of $50~\mathrm{A}$ distributed uniformly over its cross-section. Plot the magnetic field as a function of the radial distance $r$ from the center of the conductor.

48. A portion of a long, cylindrical coaxial cable is shown in the accompanying figure. A current $I$ flows down the center conductor, and this current is returned in the outer conductor. Determine the magnetic field in the regions (a) $r\leqr_1,$ (b) $r_2\geqr\geqr_1,$ (c) $r_3\geqr\geqr_2,$ and (d) $r\geqr_3.$ Assume that the current is distributed uniformly over the cross sections of the two parts of the cable.

Figure shows a long, cylindrical coaxial cable. Radius of the inner center conductor is r1. Distance from the center to the inner side of the shield is r2. Distance from the center to the outer side of the shield is r3.

9.6 Solenoids and Toroids

49. A solenoid is wound with $200$ turns per meter. When the current is $5.2~\mathrm{A},$ what is the magnetic field within the solenoid?

50. A solenoid has $12$ turns per centimeter. What current will produce a magnetic field of $2.0\times10^{-2}~\mathrm{T}$ within the solenoid?

51. If a current is $2.0~\mathrm{A},$ how many turns per centimeter must be wound on a solenoid in order to produce a magnetic field of $2.0\times10^{-3}~\mathrm{T}$ within it?

52. A solenoid is $40~\mathrm{cm}$ long, has a diameter of $3.0~\mathrm{cm},$ and is wound with $500$ turns. If the current through the windings is $4.0~\mathrm{A},$ what is the magnetic field at a point on the axis of the solenoid that is (a) at the center of the solenoid, (b) $10.0~\mathrm{cm}$ from one end of the solenoid, and (c) $5.0~\mathrm{cm}$ from one end of the solenoid? (d) Compare these answers with the infinite-solenoid case.

53. Determine the magnetic field on the central axis at the opening of a semi-infinite solenoid. (That is, take the opening to be at $x=0$ and the other end to be at

$x=\infty.)$

54. By how much is the approximation $B=\mu_0nI$ in error at the center of a solenoid that is $15.0~\mathrm{cm}$ long, has a diameter of $4.0~\mathrm{cm},$ is wrapped with $n$ turns per meter, and carries a current $I$ ?

55. A solenoid with $25$ turns per centimeter carries a current $I.$ An electron moves within the solenoid in a circle that has a radius of $2.0~\mathrm{cm}$ and is perpendicular to the axis of the solenoid. If the speed of the electron is $2.0\times10^5~\mathrm{m/s},$ what is $I$ ?

56. A toroid has $250$ turns of wire and carries a current of $20~\mathrm{A}.$ Its inner and outer radii are $8.0$ and $9.0~\mathrm{cm}.$ What are the values of its magnetic field at $r=8.1,8.5,$ and $8.9~\mathrm{cm}$ ?

57. A toroid with a square cross section $3.0~\mathrm{cm}\times3.0~\mathrm{cm}$ has an inner radius of $25.0~\mathrm{cm}.$ It is wound with $500$ turns of wire, and it carries a current of $2.0~\mathrm{A}.$ What is the strength of the magnetic field at the center of the square cross section?

9.7 Magnetism in Matter

58. The magnetic field in the core of an air-filled solenoid is $1.50~\mathrm{T}.$ By how much will this magnetic field decrease if the air is pumped out of the core while the current is held constant?

59. A solenoid has a ferromagnetic core, $n=100$ turns per metre, and $I=5.0~\mathrm{A}.$ If $B$ inside the solenoid is $2.0~\mathrm{T},$ what is $\chi$ for the core material?

60. A $20{\text -}\mathrm{A}$ current flows through a solenoid with $200$ turns per meter. What is the magnetic field inside the solenoid if its core is (a) a vacuum and (b) filled with liquid oxygen at $90~\mathrm{K}$ ?

61. The magnetic dipole moment of the iron atom is about $2.1\times10^{-23}~\mathrm{A}\cdot\mathrm{m^2}.$ (a) Calculate the maximum magnetic dipole moment of a domain consisting of $10^{19}$ iron atoms. (b) What current would have to flow through a single circular loop of wire of diameter $1.0~\mathrm{cm}$ to produce this magnetic dipole moment?

62. Suppose you wish to produce a $1.2{\text -}\mathrm{T}$ magnetic field in a toroid with an iron core for which $\chi=4.0\times10^3.$ The toroid has a mean radius of $15~\mathrm{cm}$ and is wound with $500$ turns. What current is required?

63. A current of $1.5~\mathrm{A}$ flows through the windings of a large, thin toroid with $200$ turns per meter. If the toroid is filled with iron for which $\chi=3.0\times10^3,$ what is the magnetic field within it?

64. A solenoid with an iron core is $25~\mathrm{cm}$ long and is wrapped with $100$ turns of wire. When the current through the solenoid is $10~\mathrm{A},$ the magnetic field inside it is $2.0~\mathrm{T}.$ For this current, what is the permeability of the iron? If the current is turned off and then restored to $10~\mathrm{A},$ will the magnetic field necessarily return to $2.0~\mathrm{T}$ ?

Additional Problems

65. Three long, straight, parallel wires, all carrying $20~\mathrm{A},$ are positioned as shown in the accompanying figure. What is the magnitude of the magnetic field at the point $P$ ?

This figure shows three long, straight, parallel wires. Each wire forms a vertex of an equilateral triangle with 10 centimeter sides. Point P is the center of a triangle.

66. A current $I$ flows around a wire bent into the shape of a square of side $a.$ What is the magnetic field at the point P that is a distance $z$ above the center of the square (see the accompanying figure)?

This figure shows a wire bent into the shape of a rhombus of side a. Point P that is a distance z above the center of the rhombus.

67. The accompanying figure shows a long, straight wire carrying a current of $10~\mathrm{A}.$ What is the magnetic force on an electron at the instant it is $20~\mathrm{cm}$ from the wire, traveling parallel to the wire with a speed of $2.0\times10^5~\mathrm{m/s}$ ? Describe qualitatively the subsequent motion of the electron.

Figure shows a long, straight wire carrying a current. An electron is located 20 cm from the wire and travels parallel to it.

68. Current flows along a thin, infinite sheet as shown in the accompanying figure. The current per unit length along the sheet is $J$ in amperes per meter. (a) Use the Biot-Savart law to show that $B=\mu_0J/2$ on either side of the sheet. What is the direction of $\vec{\mathbf{B}}$ on each side? (b) Now use Ampère’s law to calculate the field.

Figure shows current flowing along a thin, infinite sheet.

69. (a) Use the result of the previous problem to calculate the magnetic field between, above, and below the pair of infinite sheets shown in the accompanying figure. (b) Repeat your calculations if the direction of the current in the lower sheet is reversed.

Figure shows currents flowing along two thin, infinite sheets. Sheets are located in the parallel planes and current flows in the same direction.

70. We often assume that the magnetic field is uniform in a region and zero everywhere else. Show that in reality it is impossible for a magnetic field to drop abruptly to zero, as illustrated in the accompanying figure. (Hint: Apply Ampère’s law over the path shown.)

Figure shows the magnetic field that is perpendicular to the rectangular current path and intersects it.

71. How is the percentage change in the strength of the magnetic field across the face of the toroid related to the percentage change in the radial distance from the axis of the toroid?

72. Show that the expression for the magnetic field of a toroid reduces to that for the field of an infinite solenoid in the limit that the central radius goes to infinity.

73. A toroid with an inner radius of $20~\mathrm{cm}$ and an outer radius of $22~\mathrm{cm}$ is tightly wound with one layer of wire that has a diameter of $0.25~\mathrm{mm}.$ (a) How many turns are there on the toroid? (b) If the current through the toroid windings is $2.0~\mathrm{A},$ what is the strength of the magnetic field at the center of the toroid?

74. A wire element has $d\vec{\mathbf{l}},$ $Id\vec{\mathbf{l}}=\vec{\mathbf{J}}Adl=\vec{\mathbf{J}}dv,$ where $A$ and $dv$ are the cross-sectional area and volume of the element, respectively. Use this, the Biot-Savart law, and $\vec{\mathbf{J}}=ne\vec{\mathbf{v}}$ to show that the magnetic field of a moving point charge $q$ is given by:

$\vec{\mathbf{B}}=\frac{\mu_0}{4\pi}\frac{q\vec{\mathbf{v}}\times\hat{\mathbf{r}}}{r^2}$

75. A reasonably uniform magnetic field over a limited region of space can be produced with the Helmholtz coil, which consists of two parallel coils centered on the same axis. The coils are connected so that they carry the same current $I.$ Each coil has $N$ turns and radius $R,$ which is also the distance between the coils. (a) Find the magnetic field at any point on the $z$ -axis shown in the accompanying figure. (b) Show that $dB/dz$ and $d^2B/dz^2$ are both zero at $z=0.$ (These vanishing derivatives demonstrate that the magnetic field varies only slightly near $z=0.$ )

This picture shows two parallel coils centered on the same axis that carry the same current I. Each coil has radius R, which is also the distance between the coils.

76. A charge of $4.0~\mu\mathrm{C}$ is distributed uniformly around a thin ring of insulating material. The ring has a radius of $0.20~\mathrm{m}$ and rotates at $2.0\times10^4~\mathrm{rev/min}$ around the axis that passes through its center and is perpendicular to the plane of the ring. What is the magnetic field at the center of the ring?

77. A thin, nonconducting disk of radius $R$ is free to rotate around the axis that passes through its center and is perpendicular to the face of the disk. The disk is charged uniformly with a total charge $q.$ If the disk rotates at a constant angular velocity $\omega},$ what is the magnetic field at its center?

78. Consider the disk in the previous problem. Calculate the magnetic field at a point on its central axis that is a distance $y$ above the disk.

79. Consider the axial magnetic field $B_v=\mu_0IR^2/2(y^2+R^2)^{3/2}$ of the circular current loop shown below. (a) Evaluate $\int_{-a}^aB_ydy.$ Also show that $\lim_{a\rightarrow\infty}\int_{-a}^aBydy=\mu_0I.$ (b) Can you deduce this limit without evaluating the integral? (Hint: See the accompanying figure.)

This picture shows the circular current loop I with the magnetic field B perpendicular to the plane of the loop.

80. The current density in the long, cylindrical wire shown in the accompanying figure varies with distance $r$ from the center of the wire according to $J=cr,$ where $c$ is a constant. (a) What is the current through the wire? (b) What is the magnetic field produced by this current for $r\leq R$ ? For $r\geq R$ ?

This figure shows a long, straight, cylindrical wire with a radius R that has current I flowing through it.

81. A long, straight, cylindrical conductor contains a cylindrical cavity whose axis is displaced by a from the axis of the conductor, as shown in the accompanying figure. The current density in the conductor is given by $\vec{\mathbf{J}}=J_0\hat{\mathbf{k}},$ where $J_0$ is a constant and $\hat{\mathbf{k}}$ is along the axis of the conductor. Calculate the magnetic field at an arbitrary point $\mathrm{P}$ in the cavity by superimposing the field of a solid cylindrical conductor with radius $R_1$ and current density $\vec{\mathbf{J}}.$ onto the field of a solid cylindrical conductor with radius $R_2$ and current density $-\vec{\mathbf{J}}.$ Then use the fact that the appropriate azimuthal unit vectors can be expressed as $\hat{\pmb{\uptheta}}_1=\hat{\mathbf{k}}\times\hat{\mathbf{r}}_1$ and $\hat{\pmb{\uptheta}}_2=\hat{\mathbf{k}}\times\hat{\mathbf{r}}_2$ to show that everywhere inside the cavity the magnetic field is given by the constant $\vec{\mathbf{B}}=\frac{1}{2}\mu_0J_0\hat{\mathbf{k}}\times\vec{\mathbf{a}},$ where $\vec{\mathbf{a}}=\vec{\mathbf{r}}_1-\vec{\mathbf{r}}_2$ and $\vec{\mathbf{r}}_1=r_1\hat{\mathbf{r}}_1$ is the position of $\mathrm{P}$ relative to the centre of the conductor and $\vec{\mathbf{r}}_2=r_2\hat{\mathbf{r}}_2$ is the position of $\mathrm{P}$ relative to the centre of the cavity.

This figure shows a large circle with a radius R1 that has a circular hole of radius R2 in it at a distance a from the center. Point P is located in a hole at the distance r2 from the center of a hole and at a distance r1 from the center of a large circle.

82. Between the two ends of a horseshoe magnet the field is uniform as shown in the diagram. As you move out to outside edges, the field bends. Show by Ampère’s law that the field must bend and thereby the field weakens due to these bends.

This figure shows a horse shoe magnet with the magnetic lines going from the North end to the South end.

83. Show that the magnetic field of a thin wire and that of a current loop are zero if you are infinitely far away.

84. An Ampère loop is chosen as shown by dashed lines for a parallel constant magnetic field as shown by solid arrows. Calculate $\vec{\mathbf{B}}\cdot\vec{d\mathbf{l}}$ for each side of the loop then find the entire $\oint\vec{\mathbf{B}}\cdot\vec{d\mathbf{l}}.$ Can you think of an Ampère loop that would make the problem easier? Do those results match these?

This figure shows an Ampere loop that is located in the constant magnetic field. One of the sides of the loop forms an angle theta with the magnetic line.

85. A very long, thick cylindrical wire of radius $R$ carries a current density $J$ that varies across its cross-section. The magnitude of the current density at a point a distance $r$ from the center of the wire is given by $J=J_0\frac{r}{R},$ where $J_0$ is a constant. Find the magnetic field (a) at a point outside the wire and (b) at a point inside the wire. Write your answer in terms of the net current $I$ through the wire.

86. A very long, cylindrical wire of radius $a$ has a circular hole of radius $b$ in it at a distance $d$ from the center. The wire carries a uniform current of magnitude $I$ through it. The direction of the current in the figure is out of the paper. Find the magnetic field (a) at a point at the edge of the hole closest to the center of the thick wire, (b) at an arbitrary point inside the hole, and (c) at an arbitrary point outside the wire. (Hint: Think of the hole as a sum of two wires carrying current in the opposite directions.)

This figure shows a circle with a radius a that has a circular hole of radius b in it at a distance d from the center.

87. Magnetic field inside a torus. Consider a torus of rectangular cross-section with inner radius $a$ and outer radius $b.$ $N$ turns of an insulated thin wire are wound evenly on the torus tightly all around the torus and connected to a battery producing a steady current $I$ in the wire. Assume that the current on the top and bottom surfaces in the figure is radial, and the current on the inner and outer radii surfaces is vertical. Find the magnetic field inside the torus as a function of radial distance $r$ from the axis.

88. Two long coaxial copper tubes, each of length $L,$ are connected to a battery of voltage $V.$ The inner tube has inner radius $a$ and outer radius $b,$ and the outer tube has inner radius $c$ and outer radius $d.$ The tubes are then disconnected from the battery and rotated in the same direction at angular speed of $\omega$ radians per second about their common axis. Find the magnetic field (a) at a point inside the space enclosed by the inner tube $r<a,$ and (b) at a point between the tubes $b<r<c,$ and (c) at a point outside the tubes $r>d.$ (Hint: Think of copper tubes as a capacitor and find the charge density based on the voltage applied, $Q=VC,~C=\frac{2\pi\epsilon_0L}{\mathrm{ln}(c/b)}.)$

Challenge Problems

89. The accompanying figure shows a flat, infinitely long sheet of width $a$ that carries a current $I$ uniformly distributed across it. Find the magnetic field at the point P, which is in the plane of the sheet and at a distance $x$ from one edge. Test your result for the limit $a\rightarrow0.$

This picture shows a flat, infinitely long sheet of width a that carries a current I uniformly distributed across it. Point P is in the plane of the sheet and at a distance x from one edge.

90. A hypothetical current flowing in the $z$ -direction creates the field $\vec{\mathbf{B}}=C\left[\left(x/y^2\right)\hat{\mathbf{i}}+\left(1/y\right)\hat{\mathbf{j}}\right]$ in the rectangular region of the $xy$ -plane shown in the accompanying figure. Use Ampère’s law to find the current through the rectangle.

This figure shows the rectangular region of the xy-plane; z axis is perpendicular to the plane. Points a1 and a2 are located at the x axis. Points b1 and b2 are located at the y axis. There is an equal distance between all points.

91. A nonconducting hard rubber circular disk of radius $R$ is painted with a uniform surface charge density $\sigma.$ It is rotated about its axis with angular speed $\omega.$ (a) Find the magnetic field produced at a point on the axis a distance $h$ meters from the center of the disk. (b) Find the numerical value of magnitude of the magnetic field when $\sigma=1~\mathrm{C/m^2},$ $R=20~\mathrm{cm},$ $h=2~\mathrm{cm},$ and $\omega=400~\mathrm{rad/sec},$ and compare it with the magnitude of magnetic field of Earth, which is about $1/2~\mathrm{Gauss}.$