Chapter 13 Review

Samuel J. Ling; Jeff Sanny; William Moebs; Daryl Janzen

Chapter 13 Review

Key Terms

displacement current
extra term in Maxwell’s equations that is analogous to a real current but accounts for a changing electric field producing a magnetic field, even when the real current is present

gamma ray ( $\gamma$ ray)
extremely high frequency electromagnetic radiation emitted by the nucleus of an atom, either from natural nuclear decay or induced nuclear processes in nuclear reactors and weapons; the lower end of the $\gamma$ ray frequency range overlaps the upper end of the X-ray range, but $\gamma$ rays can have the highest frequency of any electromagnetic radiation

infrared radiation
region of the electromagnetic spectrum with a frequency range that extends from just below the red region of the visible light spectrum up to the microwave region, or from $0.74~\mu\mathrm{m}$ to $300~\mu\mathrm{m}$

Maxwell’s equations
set of four equations that comprise a complete, overarching theory of electromagnetism

microwaves
electromagnetic waves with wavelengths in the range from $1~\mathrm{mm}$ to $1~\mathrm{m}$ ; they can be produced by currents in macroscopic circuits and devices

Poynting vector
vector equal to the cross product of the electric-and magnetic fields, that describes the flow of electromagnetic energy through a surface

radar
common application of microwaves; radar can determine the distance to objects as diverse as clouds and aircraft, as well as determine the speed of a car or the intensity of a rainstorm

radiation pressure
force divided by area applied by an electromagnetic wave on a surface

radio waves
electromagnetic waves with wavelengths in the range from $1~\mathrm{mm}$ to $100~\mathrm{km}$ ; they are produced by currents in wires and circuits and by astronomical phenomena

thermal agitation
thermal motion of atoms and molecules in any object at a temperature above absolute zero, which causes them to emit and absorb radiation

ultraviolet radiation
electromagnetic radiation in the range extending upward in frequency from violet light and overlapping with the lowest X-ray frequencies, with wavelengths from $400~\mathrm{nm}$ down to about $10~\mathrm{nm}$

visible light
narrow segment of the electromagnetic spectrum to which the normal human eye responds, from about $400$ to $750~\mathrm{nm}$

X-ray
invisible, penetrating form of very high frequency electromagnetic radiation, overlapping both the ultraviolet range and the $\gamma$ -ray range

Key Equations

Displacement current	$I_{\mathrm{d}}=\epsilon_0\frac{d\Phi_{\mathrm{E}}}{dt}}$
Gauss’s law	$\oint\vec{\mathbf{E}}\cdot d\vec{\mathbf{A}}=\frac{Q_{\mathrm{in}}}{\epsilon_0}$
Gauss’s law for magnetism	$\oint\vec{\mathbf{B}}\cdot d\vec{\mathbf{A}}=0$
Faraday’s law	$\oint\vec{\mathbf{E}}\cdot d\vec{\mathbf{s}}=-\frac{d\Phi_{\mathrm{in}}}{dt}$
Ampère-Maxwell law	$\oint\vec{\mathbf{B}}\cdot d\vec{\mathbf{s}}=\mu_0I+\epsilon_0\mu_0\frac{d\Phi_{\mathrm{E}}}{dt}$
Wave equation for plane EM wave	$\frac{\partial^2E_y}{\partial x^2}=\epsilon_0\mu_0\frac{\partial^2E_y}{\partial t^2}$
Speed of EM waves	$c=\frac{1}{\sqrt{\epsilon_0\mu_0}}$
Ratio of $E$ field to $B$ field in electromagnetic wave	$c=\frac{E}{B}$
Energy flux (Poynting) vector	$\vec{\mathbf{S}}=\frac{1}{\mu_0}\vec{\mathbf{E}}\times\vec{\mathbf{B}}$
Average intensity of an electromagnetic wave	$I=S_{\mathrm{avg}}=\frac{c\epsilon_0E_0^2}{2}=\frac{cB_0^2}{2\mu_0}=\frac{E_0B_0}{2\mu_0}$
Radiation pressure	$p=\left\{\begin{array}{ll}I/c&\mathrm{Perfect~absorber}\\2I/c&\mathrm{Perfect~reflector}\end{array}\right.$

Summary

13.1 Maxwell’s Equations and Electromagnetic Waves

Maxwell’s prediction of electromagnetic waves resulted from his formulation of a complete and symmetric theory of electricity and magnetism, known as Maxwell’s equations.
The four Maxwell’s equations together with the Lorentz force law encompass the major laws of electricity and magnetism. The first of these is Gauss’s law for electricity; the second is Gauss’s law for magnetism; the third is Faraday’s law of induction (including Lenz’s law); and the fourth is Ampère’s law in a symmetric formulation that adds another source of magnetism, namely changing electric fields.
The symmetry introduced between electric and magnetic fields through Maxwell’s displacement current explains the mechanism of electromagnetic wave propagation, in which changing magnetic fields produce changing electric fields and vice versa.
Although light was already known to be a wave, the nature of the wave was not understood before Maxwell. Maxwell’s equations also predicted electromagnetic waves with wavelengths and frequencies outside the range of light. These theoretical predictions were first confirmed experimentally by Heinrich Hertz.

13.2 Plane Electromagnetic Waves

Maxwell’s equations predict that the directions of the electric and magnetic fields of the wave, and the wave’s direction of propagation, are all mutually perpendicular. The electromagnetic wave is a transverse wave.
The strengths of the electric and magnetic parts of the wave are related by 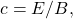$c=E/B,$ which implies that the magnetic field 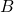$B$ is very weak relative to the electric field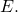 $E.$
Accelerating charges create electromagnetic waves (for example, an oscillating current in a wire produces electromagnetic waves with the same frequency as the oscillation).

13.3 Energy Carried by Electromagnetic Waves

The energy carried by any wave is proportional to its amplitude squared. For electromagnetic waves, this means intensity can be expressed as
$I=\frac{c\epsilon_0E_0^2}{2}$

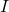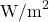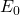where $I$ is the average intensity in $\mathrm{W/m}^2$ and $E_0$ is the maximum electric field strength of a continuous sinusoidal wave. This can also be expressed in terms of the maximum magnetic field strength 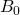$B_0$ as
$I=\frac{cB_0^2}{2\mu_0}$
and in terms of both electric and magnetic fields as

$I=\frac{E_0B_0}{2\mu_0}.$

The three expressions for 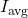$I_{\mathrm{avg}}$ are all equivalent.

13.4 Momentum and Radiation Pressure

Electromagnetic waves carry momentum and exert radiation pressure.
The radiation pressure of an electromagnetic wave is directly proportional to its energy density.
The pressure is equal to twice the electromagnetic energy intensity if the wave is reflected and equal to the incident energy intensity if the wave is absorbed.

13.5 The Electromagnetic Spectrum

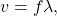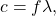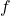The relationship among the speed of propagation, wavelength, and frequency for any wave is given by $v=f\lambda,$ so that for electromagnetic waves, $c=f\lambda,$ where $f$ is the frequency, 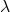$\lambda$ is the wavelength, and $c$ is the speed of light.
The electromagnetic spectrum is separated into many categories and subcategories, based on the frequency and wavelength, source, and uses of the electromagnetic waves.

Answers to Check Your Understanding

13.1 It is greatest immediately after the current is switched on. The displacement current and the magnetic field from it are proportional to the rate of change of electric field between the plates, which is greatest when the plates first begin to charge.

13.2 No. The changing electric field according to the modified version of Ampère’s law would necessarily induce a changing magnetic field.

13.3 (1) Faraday’s law, (2) the Ampère-Maxwell law

13.4 a. The directions of wave propagation, of the $E$ field, and of $B$ field are all mutually perpendicular. b. The speed of the electromagnetic wave is the speed of light $c=1/\sqrt{\epsilon_0\mu_0}$ independent of frequency. c. The ratio of electric and magnetic field amplitudes is $E/B=c.$

13.5 Its acceleration would decrease because the radiation force is proportional to the intensity of light from the Sun, which decreases with distance. Its speed, however, would not change except for the effects of gravity from the Sun and planets.

13.6 They fall into different ranges of wavelength, and therefore also different corresponding ranges of frequency.

Conceptual Questions

13.1 Maxwell’s Equations and Electromagnetic Waves

1. Explain how the displacement current maintains the continuity of current in a circuit containing a capacitor.

2. Describe the field lines of the induced magnetic field along the edge of the imaginary horizontal cylinder shown below if the cylinder is in a spatially uniform electric field that is horizontal, pointing to the right, and increasing in magnitude.

Figure shows a cylinder placed horizontally. There are three columns of arrows labeled vector E across the cylinder. The arrows point right. The column to the left has the shortest arrows and that to the right has the longest.

3. Why is it much easier to demonstrate in a student lab that a changing magnetic field induces an electric field than it is to demonstrate that a changing electric field produces a magnetic field?

13.2 Plane Electromagnetic Waves

4. If the electric field of an electromagnetic wave is oscillating along the $z$ -axis and the magnetic field is oscillating along the $x$ -axis, in what possible direction is the wave traveling?

5. In which situation shown below will the electromagnetic wave be more successful in inducing a current in the wire? Explain.

Figures a and b show electromagnetic waves with both electic and magnetic components. In figure a, the electric field is parallel to the wire and the magnetic field is perpendicular. In figure b, the magnetic field is parallel to the wire and the electric field is perpendicular.

6. In which situation shown below will the electromagnetic wave be more successful in inducing a current in the loop? Explain.

Figures a and b show electromagnetic waves with both electic and magnetic components going through a loop connected to a tuner. In figure a, the electric field is parallel to the loop and the magnetic field is perpendicular. In figure b, the magnetic field is parallel to the loop and the electric field is perpendicular.

7. Under what conditions might wires in a circuit where the current flows in only one direction emit electromagnetic waves?

8. Shown below is the interference pattern of two radio antennas broadcasting the same signal. Explain how this is analogous to the interference pattern for sound produced by two speakers. Could this be used to make a directional antenna system that broadcasts preferentially in certain directions? Explain.

Figure shows waves as circles radiating from two points lying side by side. The points where the circles intersect are higlighted and labeled constructive interference. Arrows connecting the points of constructive interference radiate outwards. These are labeled direction of constructive interference.

13.3 Energy Carried by Electromagnetic Waves

9. When you stand outdoors in the sunlight, why can you feel the energy that the sunlight carries, but not the momentum it carries?

10. How does the intensity of an electromagnetic wave depend on its electric field? How does it depend on its magnetic field?

11. What is the physical significance of the Poynting vector?

12. A $2.0{\text -}\mathrm{mW}$ helium-neon laser transmits a continuous beam of red light of cross-sectional area $0.25~\mathrm{cm}^2.$ If the beam does not diverge appreciably, how would its rms electric field vary with distance from the laser? Explain.

13.4 Momentum and Radiation Pressure

13. Why is the radiation pressure of an electromagnetic wave on a perfectly reflecting surface twice as large as the pressure on a perfectly absorbing surface?

14. Why did the early Hubble Telescope photos of Comet Ison approaching Earth show it to have merely a fuzzy coma around it, and not the pronounced double tail that developed later (see below)?

(Figure 13.6.1) $\begin{gather*}.\end{gather*}$

A Hubble Telescope photo of a comet. It appears as a bright dot with fuzzy light around it. — **Figure 13.6.1** (credit: ESA, Hubble)

15. (a) If the electric field and magnetic field in a sinusoidal plane wave were interchanged, in which direction relative to before would the energy propagate?

(b) What if the electric and the magnetic fields were both changed to their negatives?

13.5 The Electromagnetic Spectrum

16. Compare the speed, wavelength, and frequency of radio waves and X-rays traveling in a vacuum.

17. Accelerating electric charge emits electromagnetic radiation. How does this apply in each case: (a) radio waves, (b) infrared radiation.

18. Compare and contrast the meaning of the prefix “micro” in the names of SI units in the term microwaves.

19. Part of the light passing through the air is scattered in all directions by the molecules comprising the atmosphere. The wavelengths of visible light are larger than molecular sizes, and the scattering is strongest for wavelengths of light closest to sizes of molecules.

(a) Which of the main colors of light is scattered the most? (b) Explain why this would give the sky its familiar background color at midday.

20. When a bowl of soup is removed from a microwave oven, the soup is found to be steaming hot, whereas the bowl is only warm to the touch. Discuss the temperature changes that have occurred in terms of energy transfer.

21. Certain orientations of a broadcast television antenna give better reception than others for a particular station. Explain.

22. What property of light corresponds to loudness in sound?

23. Is the visible region a major portion of the electromagnetic spectrum?

24. Can the human body detect electromagnetic radiation that is outside the visible region of the spectrum?

25. Radio waves normally have their $E$ and $B$ fields in specific directions, whereas visible light usually has its $E$ and $B$ fields in random and rapidly changing directions that are perpendicular to each other and to the propagation direction. Can you explain why?

26. Give an example of resonance in the reception of electromagnetic waves.

27. Illustrate that the size of details of an object that can be detected with electromagnetic waves is related to their wavelength, by comparing details observable with two different types (for example, radar and visible light).

28. In which part of the electromagnetic spectrum are each of these waves:

(a) $f =10.0~\mathrm{kHz},$ (b) $\lambda=750~\mathrm{nm},$

(c) $f=1.25\times10^8~\mathrm{Hz},$ (d) $0.30~\mathrm{nm}$

29. In what range of electromagnetic radiation are the electromagnetic waves emitted by power lines in a country that uses $50{\text -}\mathrm{Hz}$ ac current?

30. If a microwave oven could be modified to merely tune the waves generated to be in the infrared range instead of using microwaves, how would this affect the uneven heating of the oven?

31. A leaky microwave oven in a home can sometimes cause interference with the homeowner’s WiFi system. Why?

32. When a television news anchor in a studio speaks to a reporter in a distant country, there is sometimes a noticeable lag between when the anchor speaks in the studio and when the remote reporter hears it and replies. Explain what causes this delay.

Problems

13.1 Maxwell’s Equations and Electromagnetic Waves

33. Show that the magnetic field at a distance r from the axis of two circular parallel plates, produced by placing charge $Q(t)$ on the plates is

$B_{\mathrm{ind}}=\frac{\mu_0}{2\pi r}\frac{dQ(t)}{dt}.$

34. Express the displacement current in a capacitor in terms of the capacitance and the rate of change of the voltage across the capacitor.

35. A potential difference $V(t)=V_0\sin\omega t$ is maintained across a parallel-plate capacitor with capacitance $C$ consisting of two circular parallel plates. A thin wire with resistance $R$ connects the centres of the two plates, allowing charge to leak between plates while they are charging.

(a) Obtain expressions for the leakage current $I_{\mathrm{res}}(t)$ in the thin wire. Use these results to obtain an expression for the current $I_{\mathrm{real}}(t)$ in the wires connected to the capacitor.

(b) Find the displacement current in the space between the plates from the changing electric field between the plates.

(c) Compare $I_{\mathrm{real}}(t)$ with the sum of the displacement current $I_{\mathrm{d}}(t)$ and resistor current $I_{\mathrm{res}}(t)$ between the plates, and explain why the relationship you observe would be expected.

36. Suppose the parallel-plate capacitor shown below is accumulating charge at a rate of $0.010~\mathrm{C/s}.$ What is the induced magnetic field at a distance of $10~\mathrm{cm}$ from the capacitor?

Figure shows a capacitor with two circular parallel plates. A wire is connected to each plate. A current I flows through the wire. A point below the capacitor is highlighted. This is 10 cm from the centre of the plates.

37. The potential difference $V(t)$ between parallel plates shown above is instantaneously increasing at a rate of $10&7~\mathrm{V/s}.$ What is the displacement current between the plates if the separation of the plates is $1.00~\mathrm{cm}$ and they have an area of $0.200~\mathrm{m}^2$ ?

38. A parallel-plate capacitor has a plate area of $A=0.250~\mathrm{m}^2$ and a separation of $0.0100\mathrm{m}.$ What must be must be the angular frequency $\omega$ for a voltage $V(t)=V_0\sin\omega t$ with $V_0=100~\mathrm{V}$ to produce a maximum displacement induced current of $1.00~\mathrm{A}$ between the plates?

39. The voltage across a parallel-plate capacitor with area $A=800~\mathrm{cm}^2$ and separation $d=2~\mathrm{mm}$ varies sinusoidally as $V=(15~\mathrm{mV})\cos(150t),$ where $t$ is in seconds. Find the displacement current between the plates.

40. The voltage across a parallel-plate capacitor with area $A$ and separation $d$ varies with time $t$ as $V=at^2,$ where $a$ is a constant. Find the displacement current between the plates.

16.2 Plane Electromagnetic Waves

41. If the Sun suddenly turned off, we would not know it until its light stopped coming. How long would that be, given that the Sun is $1.496\times10^{11}~\mathrm{m}$ away?

42. What is the maximum electric field strength in an electromagnetic wave that has a maximum magnetic field strength of $5.00\times10^{-4}~\mathrm{T}$ (about $10$ times Earth’s magnetic field)?

43. An electromagnetic wave has a frequency of $12~\mathrm{MHz}.$ What is its wavelength in vacuum?

44. If electric and magnetic field strengths vary sinusoidally in time at frequency $1.00~\mathrm{GHz},$ being zero at $t=0,$ then $E=E_0\sin2\pi ft$ and $B=B_0\sin2\pi ft.$ (a) When are the field strengths next equal to zero? (b) When do they reach their most negative value? (c) How much time is needed for them to complete one cycle?

45. The electric field of an electromagnetic wave traveling in vacuum is described by the following wave function:

$\vec{\mathbf{E}}=(5.00~\mathrm{V/m})\cos\left[kx-\left(6.00\times10^9~\mathrm{s}^{-1}\right)t+0.40\right]\hat{\mathbf{j}}$

where $k$ is the wavenumber in $\mathrm{rad/m},$ $x$ is in $\mathrm{m},$ $t$ is in $s.$

Find the following quantities:

(a) amplitude

(b) frequency

(c) wavelength

(d) the direction of the travel of the wave

(e) the associated magnetic field wave

46. A plane electromagnetic wave of frequency $20~\mathrm{GHz}$ moves in the positive $y$ -axis direction such that its electric field is pointed along the $z$ -axis. The amplitude of the electric field is $10~\mathrm{V/m}.$ The start of time is chosen so that at $t=0,$ the electric field has a value $10~\mathrm{V/m}$ at the origin. (a) Write the wave function that will describe the electric field wave. (b) Find the wave function that will describe the associated magnetic field wave.

47. The following represents an electromagnetic wave traveling in the direction of the positive $y$ -axis:

$E_x=0;~E_y=E_0\cos(kx-\omega t);~E_z=0,$

$B_x=0;~B_y=0; B_z=B_0\cos(kx-\omega t).$

The wave is passing through a wide tube of circular cross-section of radius $R$ whose axis is along the $y$ -axis. Find the expression for the displacement current through the tube.

13.3 Energy Carried by Electromagnetic Waves

48. While outdoors on a sunny day, a student holds a large convex lens of radius $4.0~\mathrm{cm}$ above a sheet of paper to produce a bright spot on the paper that is $1.0~\mathrm{cm}$ in radius, rather than a sharp focus. By what factor is the electric field in the bright spot of light related to the electric field of sunlight leaving the side of the lens facing the paper?

49. A plane electromagnetic wave travels northward. At one instant, its electric field has a magnitude of $6.0~\mathrm{V/m}$ and points eastward. What are the magnitude and direction of the magnetic field at this instant?

50. The electric field of an electromagnetic wave is given by

$E=(6.0\times10^{-3}~\mathrm{V/m})\sin\left[2\pi\left(\frac{x}{18~\mathrm{m}}-\frac{t}{6.0\times10^{-8}~\mathrm{s}}\right)\right]\hat{\mathbf{j}}.$

Write the equations for the associated magnetic field and Poynting vector.

51. A radio station broadcasts at a frequency of $760~\mathrm{kHz}.$ At a receiver some distance from the antenna, the maximum magnetic field of the electromagnetic wave detected is $2.15\times10^{-11}~\mathrm{T}.$

(a) What is the maximum electric field? (b) What is the wavelength of the electromagnetic wave?

52. The filament in a clear incandescent light bulb radiates visible light at a power of $5.00~\mathrm{W}.$ Model the glass part of the bulb as a sphere of radius $r_0=3.00~\mathrm{cm}$ and calculate the amount of electromagnetic energy from visible light inside the bulb.

53. At what distance does a $100{\text -}\mathrm{W}$ lightbulb produce the same intensity of light as a $75{\text -}\mathrm{W}$ lightbulb produces $10~\mathrm{m}$ away? (Assume both have the same efficiency for converting electrical energy in the circuit into emitted electromagnetic energy.)

54. An incandescent light bulb emits only $2.6~\mathrm{W}$ of its power as visible light. What is the rms electric field of the emitted light at a distance of $3.0~\mathrm{m}$ from the bulb?

55. A $150{\text -}\mathrm{W}$ lightbulb emits $5\%$ of its energy as electromagnetic radiation. What is the magnitude of the average Poynting vector $10~\mathrm{m}$ from the bulb?

56. A small helium-neon laser has a power output of $2.5~\mathrm{mW}.$ What is the electromagnetic energy in a $1.0{\text -}\mathrm{m}$ length of the beam?

57. At the top of Earth’s atmosphere, the time-averaged Poynting vector associated with sunlight has a magnitude of about $1.4~\mathrm{kW/m}^2.$

(a) What are the maximum values of the electric and magnetic fields for a wave of this intensity? (b) What is the total power radiated by the sun? Assume that the Earth is $1.5\times10^{11}~\mathrm{m}$ from the Sun and that sunlight is composed of electromagnetic plane waves.

58. The magnetic field of a plane electromagnetic wave moving along the $z$ -axis is given by $\vec{\mathbf{B}}=B_0\cos(kz+\omega t)\hat{\mathbf{j}}$ where $B_0=5.00\times10^{-10}~\mathrm{T}$ and $k=3.14\times10^{-2}~\mathrm{m}^{-1}.$

(a) Write an expression for the electric field associated with the wave. (b) What are the frequency and the wavelength of the wave? (c) What is its average Poynting vector?

59. What is the intensity of an electromagnetic wave with a peak electric field strength of $125~\mathrm{V/m}$ ?

60. Assume the helium-neon lasers commonly used in student physics laboratories have power outputs of $0.500~\mathrm{mW}.$ (a) If such a laser beam is projected onto a circular spot $1.00~\mathrm{mm}$ in diameter, what is its intensity? (b) Find the peak magnetic field strength. (c) Find the peak electric field strength.

61. An AM radio transmitter broadcasts $50.0~\mathrm{kW}$ of power uniformly in all directions. (a) Assuming all of the radio waves that strike the ground are completely absorbed, and that there is no absorption by the atmosphere or other objects, what is the intensity $30.0~\mathrm{km}$ away? (Hint: Half the power will be spread over the area of a hemisphere.) (b) What is the maximum electric field strength at this distance?

62. Suppose the maximum safe intensity of microwaves for human exposure is taken to be $1.00~\mathrm{W/m}^2.$ (a) If a radar unit leaks $10.0~\mathrm{W}$ of microwaves (other than those sent by its antenna) uniformly in all directions, how far away must you be to be exposed to an intensity considered to be safe? Assume that the power spreads uniformly over the area of a sphere with no complications from absorption or reflection. (b) What is the maximum electric field strength at the safe intensity? (Note that early radar units leaked more than modern ones do. This caused identifiable health problems, such as cataracts, for people who worked near them.)

63. A $2.50{\text -}\mathrm{m}$ -diameter university communications satellite dish receives TV signals that have a maximum electric field strength (for one channel) of $7.50~\mu\mathrm{V/m}$ (see below). (a) What is the intensity of this wave? (b) What is the power received by the antenna? (c) If the orbiting satellite broadcasts uniformly over an area of $1.50\times10^{13}~\mathrm{m}^2$ (a large fraction of North America), how much power does it radiate?

Figure shows waves incident on a dish antenna.

64. Lasers can be constructed that produce an extremely high intensity electromagnetic wave for a brief time—called pulsed lasers. They are used to initiate nuclear fusion, for example. Such a laser may produce an electromagnetic wave with a maximum electric field strength of $1.00\times10^{11}~\mathrm{V/m}$ for a time of $1.00~\mathrm{ns}.$ (a) What is the maximum magnetic field strength in the wave? (b) What is the intensity of the beam? (c) What energy does it deliver on an $1.00{\text -}\mathrm{mm}^2$ area?

13.4 Momentum and Radiation Pressure

65. A $150{\text -}\mathrm{W}$ lightbulb emits $5\%$ of its energy as electromagnetic radiation. What is the radiation pressure on an absorbing sphere of radius $10~\mathrm{m}$ that surrounds the bulb?

66. What pressure does light emitted uniformly in all directions from a $100{\text -}\mathrm{W}$ incandescent light bulb exert on a mirror at a distance of $3.0~\mathrm{m},$ if $2.6~\mathrm{W}$ of the power is emitted as visible light?

67. A microscopic spherical dust particle of radius $2~\mu\mathrm{m}$ and mass $10~\mu\mathrm{g}$ is moving in outer space at a constant speed of $30~\mathrm{cm/sec}.$ A wave of light strikes it from the opposite direction of its motion and gets absorbed. Assuming the particle decelerates uniformly to zero speed in one second, what is the average electric field amplitude in the light?

68. A Styrofoam spherical ball of radius $2~\mathrm{mm}$ and mass $20~\mu\mathrm{g}$ is to be suspended by the radiation pressure in a vacuum tube in a lab. How much intensity will be required if the light is completely absorbed the ball?

69. Suppose that $\vec{\mathbf{S}}_{\mathrm{avg}}$ for sunlight at a point on the surface of Earth is $900~\mathrm{W/m}^2.$ (a) If sunlight falls perpendicularly on a kite with a reflecting surface of area $0.75~\mathrm{m}^2,$ what is the average force on the kite due to radiation pressure? (b) How is your answer affected if the kite material is black and absorbs all sunlight?

70. Sunlight reaches the ground with an intensity of about $1.0~\mathrm{kW/m}^2.$ A sunbather has a body surface area of $0.8~\mathrm{m}^2$ facing the sun while reclining on a beach chair on a clear day. (a) How much energy from direct sunlight reaches the sunbather’s skin per second? (b) What pressure does the sunlight exert if it is absorbed?

71. Suppose a spherical particle of mass $m$ and radius $R$ in space absorbs light of intensity $I$ for time $t.$ (a) How much work does the radiation pressure do to accelerate the particle from rest in the given time it absorbs the light? (b) How much energy carried by the electromagnetic waves is absorbed by the particle over this time based on the radiant energy incident on the particle?

13.5 The Electromagnetic Spectrum

72. How many helium atoms, each with a radius of about 31 pm, must be placed end to end to have a length equal to one wavelength of $470~\mathrm{nm}$ blue light?

73. If you wish to detect details of the size of atoms (about $0.2~\mathrm{nm}$ ) with electromagnetic radiation, it must have a wavelength of about this size. (a) What is its frequency? (b) What type of electromagnetic radiation might this be?

74. Find the frequency range of visible light, given that it encompasses wavelengths from $380$ to $760~\mathrm{nm}.$

75. (a) Calculate the wavelength range for AM radio given its frequency range is $540$ to $1600~\mathrm{kHz}.$ (b) Do the same for the FM frequency range of $88.0$ to $108~\mathrm{MHz}.$

76. Radio station WWVB, operated by the National Institute of Standards and Technology (NIST) from Fort Collins, Colorado, at a low frequency of $60~\mathrm{kHz},$ broadcasts a time synchronization signal whose range covers the entire continental US. The timing of the synchronization signal is controlled by a set of atomic clocks to an accuracy of $1\times10^{-12}~\mathrm{s},$ and repeats every $1$ minute. The signal is used for devices, such as radio-controlled watches, that automatically synchronize with it at preset local times. WWVB’s long wavelength signal tends to propagate close to the ground.

(a) Calculate the wavelength of the radio waves from WWVB.

(b) Estimate the error that the travel time of the signal causes in synchronizing a radio controlled watch in Norfolk, Virginia, which is $1570~\mathrm{mi}$ ( $2527~\mathrm{km}$ ) from Fort Collins, Colorado.

77. An outdoor WiFi unit for a picnic area has a $100{\text -}\mathrm{mW}$ output and a range of about $30~\mathrm{m}.$ What output power would reduce its range to $12~\mathrm{m}$ for use with the same devices as before? Assume there are no obstacles in the way and that microwaves into the ground are simply absorbed.

78. The prefix “mega” ( $\mathrm{M}$ ) and “kilo” ( $\mathrm{k}$ ), when referring to amounts of computer data, refer to factors of $1024$ or $2^{10}$ rather than $1000$ for the prefix kilo, and $1024^2=2^{20}$ rather than $1,000,000$ for the prefix mega. If a wireless (WiFi) router transfers $150~\mathrm{Mbps}$ of data, how many bits per second is that in decimal arithmetic?

79. A computer user finds that his wireless router transmits data at a rate of $75~\mathrm{Mbps}$ (megabits per second). Compare the average time to transmit one bit of data with the time difference between the wifi signal reaching an observer’s cell phone directly and by bouncing back to the observer from a wall $8.00~\mathrm{m}$ past the observer.

80. (a) The ideal size (most efficient) for a broadcast antenna with one end on the ground is one-fourth the wavelength ( $\lambda/4$ ) of the electromagnetic radiation being sent out. If a new radio station has such an antenna that is $50.0~\mathrm{m}$ high, what frequency does it broadcast most efficiently? Is this in the AM or FM band? (b) Discuss the analogy of the fundamental resonant mode of an air column closed at one end to the resonance of currents on an antenna that is one-fourth their wavelength.

81. What are the wavelengths of (a) X-rays of frequency $2.0\times10^{17}~\mathrm{Hz}$ ? (b) Yellow light of frequency $5.1\times10^{14}~\mathrm{Hz}$ ? (c) Gamma rays of frequency $1.0\times10^{23}~\mathrm{Hz}$ ?

82. For red light of $\lambda=660~\mathrm{nm},$ what are $f,$ $\omega,$ and $k$ ?

83. A radio transmitter broadcasts plane electromagnetic waves whose maximum electric field at a particular location is $1.55\times10^{-3}~\mathrm{V/m}.$ What is the maximum magnitude of the oscillating magnetic field at that location? How does it compare with Earth’s magnetic field?

84. (a) Two microwave frequencies authorized for use in microwave ovens are: $915$ and $2450~\mathrm{MHz}.$ Calculate the wavelength of each. (b) Which frequency would produce smaller hot spots in foods due to interference effects?

85. During normal beating, the heart creates a maximum $4.00{\text -}\mathrm{mV}$ potential across $0.300~\mathrm{m}$ of a person’s chest, creating a $1.00{\text -}\mathrm{Hz}$ electromagnetic wave. (a) What is the maximum electric field strength created? (b) What is the corresponding maximum magnetic field strength in the electromagnetic wave? (c) What is the wavelength of the electromagnetic wave?

86. Distances in space are often quoted in units of light-years, the distance light travels in $1$ year. (a) How many meters is a light-year? (b) How many meters is it to Andromeda, the nearest large galaxy, given that it is $2.54\times10^6~\mathrm{ly}$ away? (c) The most distant galaxy yet discovered is $13.4\times10^9~\mathrm{ly}$ away. How far is this in meters?

87. A certain $60.0{\text -}\mathrm{Hz}$ ac power line radiates an electromagnetic wave having a maximum electric field strength of $13.0~\mathrm{kV/m}.$ (a) What is the wavelength of this very-low-frequency electromagnetic wave? (b) What type of electromagnetic radiation is this wave (b) What is its maximum magnetic field strength?

88. (a) What is the frequency of the $193{\text -}\mathrm{nm}$ ultraviolet radiation used in laser eye surgery? (b) Assuming the accuracy with which this electromagnetic radiation can ablate (reshape) the cornea is directly proportional to wavelength, how much more accurate can this UV radiation be than the shortest visible wavelength of light?

Additional Problems

89. In a region of space, the electric field is pointed along the $x$ -axis, but its magnitude changes as described by

$E-x=(10~\mathrm{N/C})\sin(20x-500t),~~~E_y=E_z=0,$

where $t$ is in nanoseconds and $x$ is in $\mathrm{cm}.$ Find the displacement current through a circle of radius $3~\mathrm{cm}$ in the $x=0$ plane at $t=0.$

90. A microwave oven uses electromagnetic waves of frequency $f=2.45\times10^9~\mathrm{Hz}$ to heat foods. The waves reflect from the inside walls of the oven to produce an interference pattern of standing waves whose antinodes are hot spots that can leave observable pit marks in some foods. The pit marks are measured to be $6.0~\mathrm{cm}$ apart. Use the method employed by Heinrich Hertz to calculate the speed of electromagnetic waves this implies.

Use the Appendix D for the next two exercises

91. Galileo proposed measuring the speed of light by uncovering a lantern and having an assistant a known distance away uncover his lantern when he saw the light from Galileo’s lantern, and timing the delay. How far away must the assistant be for the delay to equal the human reaction time of about $0.25~\mathrm{s}$ ?

92. Show that the wave equation in one dimension

$\frac{\partial^2f}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2f}{\partial t^2}$

is satisfied by any doubly differentiable function of either the form $f(x-vt)$ or $f(x+vt).$

93. On its highest power setting, a microwave oven increases the temperature of $0.400~\mathrm{kg}$ of spaghetti by $45^{\circ}$ in $120~\mathrm{s}.$ (a) What was the rate of energy absorption by the spaghetti, given that its specific heat is $3.76\times10^3~\mathrm{J/kg}\cdot ^{\circ}\mathrm{C}$ ? Assume the spaghetti is perfectly absorbing. (b) Find the average intensity of the microwaves, given that they are absorbed over a circular area $20.0~\mathrm{cm}$ in diameter. (c) What is the peak electric field strength of the microwave? (d) What is its peak magnetic field strength?

94. A certain microwave oven projects $1.00~\mathrm{kW}$ of microwaves onto a $30~\mathrm{cm}\times40~\mathrm{cm}$ area. (a) What is its intensity in $\mathrm{W/m}^2$ ? (b) Calculate the maximum electric field strength $E_0$ in these waves. (c) What is the maximum magnetic field strength $B_0$ ?

95. Electromagnetic radiation from a $5.00{\text -}\mathrm{mW}$ laser is concentrated on a $1.00~\mathrm{mm}^2$ area. (a) What is the intensity in $\mathrm{W/m}^2$ ? (b) Suppose a $2.00{\text -}\mathrm{nC}$ electric charge is in the beam. What is the maximum electric force it experiences? (c) If the electric charge moves at $400~\mathrm{m/s},$ what maximum magnetic force can it feel?

96. A $200{\text -}\mathrm{turn}$ flat coil of wire $30.0~\mathrm{cm}$ in diameter acts as an antenna for FM radio at a frequency of $100~\mathrm{MHz}.$ The magnetic field of the incoming electromagnetic wave is perpendicular to the coil and has a maximum strength of $1.00\times10^{-12}~\mathrm{T}.$ (a) What power is incident on the coil? (b) What average emf is induced in the coil over one-fourth of a cycle? (c) If the radio receiver has an inductance of $2.50~\mu\mathrm{H},$ what capacitance must it have to resonate at $100~\mathrm{MHz}$ ?

97. Suppose a source of electromagnetic waves radiates uniformly in all directions in empty space where there are no absorption or interference effects. (a) Show that the intensity is inversely proportional to $r_2,$ the distance from the source squared. (b) Show that the magnitudes of the electric and magnetic fields are inversely proportional to $r.$

98. A radio station broadcasts its radio waves with a power of $50,000~\mathrm{W}.$ What would be the intensity of this signal if it is received on a planet orbiting Proxima Centuri, the closest star to our Sun, at $4.243~\mathrm{ly}$ away?

99. The Poynting vector describes a flow of energy whenever electric and magnetic fields are present. Consider a long cylindrical wire of radius $r$ with a current $I$ in the wire, with resistance $R$ and voltage $V.$ From the expressions for the electric field along the wire and the magnetic field around the wire, obtain the magnitude and direction of the Poynting vector at the surface. Show that it accounts for an energy flow into the wire from the fields around it that accounts for the Ohmic heating of the wire.

100. The Sun’s energy strikes Earth at an intensity of $1.37~\mathrm{kW/m}^2.$ Assume as a model approximation that all of the light is absorbed. (Actually, about $30\%$ of the light intensity is reflected out into space.)

(a) Calculate the total force that the Sun’s radiation exerts on Earth.

(b) Compare this to the force of gravity between the Sun and Earth.

Earth’s mass is $5.972\times10^{24}~\mathrm{kg}.$

101. If a Lightsail spacecraft were sent on a Mars mission, by what fraction would its propulsion force be reduced when it reached Mars?

102. Lunar astronauts placed a reflector on the Moon’s surface, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. (a) To what accuracy in meters can the distance to the Moon be determined, if this time can be measured to $0.100~\mathrm{ns}$ ? (b) What percent accuracy is this, given the average distance to the Moon is $384,400~\mathrm{km}$ ?

103. Radar is used to determine distances to various objects by measuring the round-trip time for an echo from the object. (a) How far away is the planet Venus if the echo time is $1000~\mathrm{s}$ ? (b) What is the echo time for a car $75.0~\mathrm{m}$ from a highway police radar unit? (c) How accurately (in nanoseconds) must you be able to measure the echo time to an airplane $12.0~\mathrm{km}$ away to determine its distance within $10.0~\mathrm{m}$ ?

104. Calculate the ratio of the highest to lowest frequencies of electromagnetic waves the eye can see, given the wavelength range of visible light is from $380$ to $760~\mathrm{nm}.$ (Note that the ratio of highest to lowest frequencies the ear can hear is $1000.$ )

105. How does the wavelength of radio waves for an AM radio station broadcasting at $1030~\mathrm{kHz}$ compare with the wavelength of the lowest audible sound waves (of $20~\mathrm{Hz}$ ). The speed of sound in air at $20~^{\circ}\mathrm{C}$ is about $343~\mathrm{m/s}.$

Challenge Problems

106. A parallel-plate capacitor with plate separation $d$ is connected to a source of emf that places a time-dependent voltage $V(t)$ across its circular plates of radius $r_0$ and area $A=\pi r^2_0$ (see below).

Figure shows a capacitor with two circular parallel plates. A wire, carrying current I, is connected across it. The radius of the plates is r subscript 0 and the distance between two plates is d.

(a) Write an expression for the time rate of change of energy inside the capacitor in terms of $V(t)$ and $dV(t)/dt.$

(b) Assuming that $V(t)$ is increasing with time, identify the directions of the electric field lines inside the capacitor and of the magnetic field lines at the edge of the region between the plates, and then the direction of the Poynting vector $\vec{\mathbf{S}}$ at this location.

(c) Obtain expressions for the time dependence of $E(t),$ for $B(t)$ from the displacement current, and for the magnitude of the Poynting vector at the edge of the region between the plates.

(d) From $\vec{\mathbf{S}},$ obtain an expression in terms of $V(t)$ and $dV(t)/dt$ for the rate at which electromagnetic field energy enters the region between the plates.

(e) Compare the results of parts (a) and (d) and explain the relationship between them.

107. A particle of cosmic dust has a density $\rho=2.0~\mathrm{g/cm}^3.$ (a) Assuming the dust particles are spherical and light absorbing, and are at the same distance as Earth from the Sun, determine the particle size for which radiation pressure from sunlight is equal to the Sun’s force of gravity on the dust particle. (b) Explain how the forces compare if the particle radius is smaller. (c) Explain what this implies about the sizes of dust particle likely to be present in the inner solar system compared with outside the Oort cloud.

License

Icon for the Creative Commons Attribution 4.0 International License