Chapter 2 Review

Samuel J. Ling; Jeff Sanny; William Moebs; Daryl Janzen

Chapter 2 Review

Key Terms

area vector
vector with magnitude equal to the area of a surface and direction perpendicular to the surface

cylindrical symmetry
system only varies with distance from the axis, not direction

electric flux
dot product of the electric field and the area through which it is passing

flux
quantity of something passing through a given area

free electrons
also called conduction electrons, these are the electrons in a conductor that are not bound to any particular atom, and hence are free to move around

Gaussian surface
any enclosed (usually imaginary) surface

planar symmetry
system only varies with distance from a plane

spherical symmetry
system only varies with the distance from the origin, not in direction

Key Equations

Definition of electric flux, for uniform electric field	$\Phi=\vec{\mathbf{E}}\cdot\vec{\mathbf{A}}\rightarrow EA\cos\theta$
Electric flux through an open surface	$\Phi=\int_S\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA=\int_S\vec{\mathbf{E}}\cdot d\vec{\mathbf{A}}$
Electric flux through a closed surface	$\Phi=\oint_S\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA=\oint_S\vec{\mathbf{E}}\cdot\vec{\mathbf{E}}\cdot d\vec{\mathbf{A}}$
Gauss’s law	$\Phi=\oint_S\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA=\frac{q_{\mathrm{enc}}}{\epsilon_0}$
Gauss’s Law for systems with symmetry	$\Phi=\oint_S\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA=E\oint_SdA=EA=\frac{q_{\mathrm{enc}}}{\epsilon_0}$
The magnitude of the electric field just outside the surface of a conductor	$E=\frac{\sigma}{\epsilon_0}$

Summary

2.1 Electric Flux

The electric flux through a surface is proportional to the number of field lines crossing that surface. Note that this means the magnitude is proportional to the portion of the field perpendicular to the area.
The electric flux is obtained by evaluating the surface integral
$\Phi=\int_S\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA=\int_S\vec{\mathbf{E}}\cdot d\vec{\mathbf{A}}$

where the notation used here is for a closed surface $S$ .

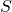2.2 Explaining Gauss’s Law

Gauss’s law relates the electric flux through a closed surface to the net charge within that surface,
$\Phi=\oint_S\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA=\frac{q_{\mathrm{enc}}}{\epsilon_0}$

where qenc is the total charge inside the Gaussian surface $S$ .
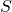All surfaces that include the same amount of charge have the same number of field lines crossing it, regardless of the shape or size of the surface, as long as the surfaces enclose the same amount of charge.

2.3 Applying Gauss’s Law

For a charge distribution with certain spatial symmetries (spherical, cylindrical, and planar), we can find a Gaussian surface over which 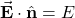$\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}=E$ , where 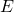$E$ is constant over the surface. The electric field is then determined with Gauss’s law.
For spherical symmetry, the Gaussian surface is also a sphere, and Gauss’s law simplifies to $4\pi r^2E=\frac{q_{\mathrm{enc}}}{\epsilon_0}$ .
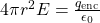For cylindrical symmetry, we use a cylindrical Gaussian surface, and find that Gauss’s law simplifies to $2\pi rLE=\frac{q_{\mathrm{enc}}}{\epsilon_0}$ .
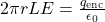For planar symmetry, a convenient Gaussian surface is a box penetrating the plane, with two faces parallel to the plane and the remainder perpendicular, resulting in Gauss’s law being $2AE=\frac{q_{\mathrm{enc}}}{\epsilon_0}$ .

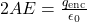2.4 Conductors in Electrostatic Equilibrium

The electric field inside a conductor vanishes.
Any excess charge placed on a conductor resides entirely on the surface of the conductor.
The electric field is perpendicular to the surface of a conductor everywhere on that surface.
The magnitude of the electric field just above the surface of a conductor is given by $E=\frac{\sigma}{\epsilon_0}$ .

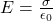Answers to Check Your Understanding

2.1. Place it so that its unit normal is perpendicular to $\vec{\mathbf{E}}$ .

2.2. $mab^2/2$ .

2.3 a. $3.4\times10^5~\mathrm{N}\cdot\mathrm{m}^2/\mathrm{C}$ ; b. $-3.4\times10^5~\mathrm{N}\cdot\mathrm{m}^2/\mathrm{C}$ ; c. $3.4\times10^5~\mathrm{N}\cdot\mathrm{m}^2/\mathrm{C}$ ; d. $0$ .

2.4. In this case, there is only $\vec{\mathbf{E}}_{\mathrm{out}}$ . So, yes.

2.5. $\vec{\mathbf{E}}=\frac{\lambda_0}{2\pi\epsilon_0}\frac{1}{d}\hat{\mathbf{r}}$ ; This agrees with the calculation of Example 1.5.1 where we found the electric field by integrating over the charged wire. Notice how much simpler the calculation of this electric field is with Gauss’s law.

2.6. If there are other charged objects around, then the charges on the surface of the sphere will not necessarily be spherically symmetrical; there will be more in certain direction than in other directions.

Conceptual Questions

2.1 Electric Flux

1. Discuss how would orient a planar surface of area $A$ in a uniform electric field of magnitude $E_0$ to obtain (a) the maximum flux and (b) the minimum flux through the area.

2. What are the maximum and minimum values of the flux in the preceding question?

3. The net electric flux crossing a closed surface is always zero. True or false?

4. The net electric flux crossing an open surface is never zero. True or false?

2.2 Explaining Gauss’s Law

5. Two concentric spherical surfaces enclose a point charge $q$ . The radius of the outer sphere is twice that of the inner one. Compare the electric fluxes crossing the two surfaces.

6. Compare the electric flux through the surface of a cube of side length $a$ that has a charge $q$ at its centre to the flux through a spherical surface of radius a with a charge $q$ at its centre.

7. (a) If the electric flux through a closed surface is zero, is the electric field necessarily zero at all points on the surface? (b) What is the net charge inside the surface?

8. Discuss how Gauss’s law would be affected if the electric field of a point charge did not vary as $1/r^2$ .

9. Discuss the similarities and differences between the gravitational field of a point mass m and the electric field of a point charge $q$ .

10. Discuss whether Gauss’s law can be applied to other forces, and if so, which ones.

11. Is the term $\vec{\mathbf{E}}$ in Gauss’s law the electric field produced by just the charge inside the Gaussian surface?

12. Reformulate Gauss’s law by choosing the unit normal of the Gaussian surface to be the one directed inward.

2.3 Applying Gauss’s Law

13. Would Gauss’s law be helpful for determining the electric field of two equal but opposite charges a fixed distance apart?

14. Discuss the role that symmetry plays in the application of Gauss’s law. Give examples of continuous charge distributions in which Gauss’s law is useful and not useful in determining the electric field.

15. Discuss the restrictions on the Gaussian surface used to discuss planar symmetry. For example, is its length important? Does the cross-section have to be square? Must the end faces be on opposite sides of the sheet?

2.4 Conductors in Electrostatic Equilibrium

16. Is the electric field inside a metal always zero?

17. Under electrostatic conditions, the excess charge on a conductor resides on its surface. Does this mean that all the conduction electrons in a conductor are on the surface?

18. A charge $q$ is placed in the cavity of a conductor as shown below. Will a charge outside the conductor experience an electric field due to the presence of $q$ ?

Figure shows an egg shape with an oval cavity within it. The cavity is surrounded by a dotted line just outside it. This is labeled S. There is a positive charge labeled q within the cavity.

19. The conductor in the preceding figure has an excess charge of $-5.0~\mu\mathrm{C}$ . If a $2.0{\text -}\mu\mathrm{C}$ point charge is placed in the cavity, what is the net charge on the surface of the cavity and on the outer surface of the conductor?

Problems

2.1 Electric Flux

20. A uniform electric field of magnitude $1.1\times10^4~\mathrm{N/C}$ is perpendicular to a square sheet with sides $2.0~\mathrm{m}$ long. What is the electric flux through the sheet?

21. Calculate the flux through the sheet of the previous problem if the plane of the sheet is at an angle of $60^{\circ}$ to the field. Find the flux for both directions of the unit normal to the sheet.

22. Find the electric flux through a rectangular area $3~\mathrm{cm}\times2~\mathrm{cm}$ between two parallel plates where there is a constant electric field of $30~\mathrm{N/C}$ for the following orientations of the area: (a) parallel to the plates, (b) perpendicular to the plates, and (c) the normal to the area making a $30^{\circ}$ angle with the direction of the electric field. Note that this angle can also be given as $180^{\circ}+30^{\circ}$ .

23. The electric flux through a square-shaped area of side $5~\mathrm{cm}$ near a large charged sheet is found to be $3\times10^{-5}~\mathrm{N}\cdot\mathrm{m}^2/\mathrm{C}$ when the area is parallel to the plate. Find the charge density on the sheet.

24. Two large rectangular aluminum plates of area $150~\mathrm{cm}^2$ face each other with a separation of $3~\mathrm{mm}$ between them. The plates are charged with equal amount of opposite charges, $\pm20~\mu\mahtrm{C}$ . The charges on the plates face each other. Find the flux through a circle of radius $3~\mathrm{cm}$ between the plates when the normal to the circle makes an angle of $5^{\circ}$ with a line perpendicular to the plates. Note that this angle can also be given as $180^{\circ}+5^{\circ}$ .

25. A square surface of area $2~\mathrm{cm}^2$ is in a space of uniform electric field of magnitude $10^3~\mathrm{N/C}$ . The amount of flux through it depends on how the square is oriented relative to the direction of the electric field. Find the electric flux through the square, when the normal to it makes the following angles with electric field: (a) $30^{\circ}$ , (b) $90^{\circ}$ and (c) $0^{\circ}$ . Note that these angles can also be given as $180^{\circ}+\theta$ .

26. A vector field is pointed along the $z$ -axis, $\vec{\mathbf{v}}=\frac{\alpha}{x^2+y^2}\hat{\mathbf{z}}$ . (a) Find the flux of the vector field through a rectangle in the $xy$ -plane between $a<x<b$ and $c<y<d$ . (b) Do the same through a rectangle in the $yz$ -plane between $a<z<b$ and $c<y<d$ . (Leave your answer as an integral.)

27. Consider the uniform electric field $\vec{\mathbf{E}}=(4.0\hat{\mathbf{j}}+3.0\hat{\mathbf{k}})\times10^3~\mathrm{N/C}$ . What is its electric flux through a circular area of radius $2.0~\mathrm{m}$ that lies in the $xy$ -plane?

28. Repeat the previous problem, given that the circular area is (a) in the $yz$ -plane and (b) $45^{\circ}$ above the $xy$ –plane.

29. An infinite charged wire with charge per unit length $\lambda$ lies along the central axis of a cylindrical surface of radius $r$ and length $l$ . What is the flux through the surface due to the electric field of the charged wire?

2.2 Explaining Gauss’s Law

30. Determine the electric flux through each surface whose cross-section is shown below.

31. Find the electric flux through the closed surface whose cross-sections are shown below.

32. A point charge $q$ is located at the centre of a cube whose sides are of length $a$ . If there are no other charges in this system, what is the electric flux through one face of the cube?

33. A point charge of $10~\mu\mathrm{C}$ is at an unspecified location inside a cube of side $2~\mathrm{cm}$ . Find the net electric flux though the surfaces of the cube.

34. A net flux of $1.0\times10^4~\mathrm{N}\cdot\mathrm{m}^2/\mathrm{C}$ passes inward through the surface of a sphere of radius $5~\mathrm{cm}$ . (a) How much charge is inside the sphere? (b) How precisely can we determine the location of the charge from this information?

35. A charge $q$ is placed at one of the corners of a cube of side $a$ , as shown below. Find the magnitude of the electric flux through the shaded face due to $q$ . Assume $a>0$ .

Figure shows a cube with length of each side equal to a. The back surface of it is shaded. One front corner has a small circle on it labeled q.

36. The electric flux through a cubical box $8.0~\mathrm{cm}$ on a side is $1.2\times10^3~\mathrm{N}\cdot\mathrm{m}^2/\mathrm{C}$ . What is the total charge enclosed by the box?

37. The electric flux through a spherical surface is $4.0\times10^4~\mathrm{N}\cdot\mathrm{m}^2/\mathrm{C}$ . What is the net charge enclosed by the surface?

38. A cube whose sides are of length $d$ is placed in a uniform electric field of magnitude $E=4.0\times10^3~\mathrm{N/C}$ so that the field is perpendicular to two opposite faces of the cube. What is the net flux through the cube?

39. Repeat the previous problem, assuming that the electric field is directed along a body diagonal of the cube.

40. A total charge $5.0\times10^{6}~\mathrm{C}$ is distributed uniformly throughout a cubical volume whose edges are $8.0~\mathrm{cm}$ long. (a) What is the charge density in the cube? (b) What is the electric flux through a cube with $12.0{\text -}\mathrm{cm}$ edges that is concentric with the charge distribution? (c) Do the same calculation for cubes whose edges are $10.0~\mathrm{cm}$ long and $5.0~\mathrm{cm}$ long. (d) What is the electric flux through a spherical surface of radius $3.0~\mathrm{cm}$ that is also concentric with the charge distribution?

2.3 Applying Gauss’s Law

41. Recall that in the example of a uniform charged sphere, $\rho_0=Q/\left(\frac{4}{3}\pi R^3\right)$ . Rewrite the answers in terms of the total charge $Q$ on the sphere.

42. Suppose that the charge density of the spherical charge distribution shown in Figure 2.3.3 is $\rho(r)=\rho_0r/R$ for $r\leq R$ and zero for $r>R$ . Obtain expressions for the electric field both inside and outside the distribution.

43. A very long, thin wire has a uniform linear charge density of $50~\mu\mathrm{C/m}$ . What is the electric field at a distance $2.0~\mathrm{cm}$ from the wire?

44. A charge of $-30~\mu\mathrm{C}$ is distributed uniformly throughout a spherical volume of radius $10.0~\mathrm{cm}$ . Determine the electric field due to this charge at a distance of (a) $2.0~\mathrm{cm}$ , (b) $5.0~\mathrm{cm}$ , and (c) $20.0~\mathrm{cm}$ from the centre of the sphere.

45. Repeat your calculations for the preceding problem, given that the charge is distributed uniformly over the surface of a spherical conductor of radius $10.0~\mathrm{cm}$ .

46. A total charge $Q$ is distributed uniformly throughout a spherical shell of inner and outer radii $r_1$ and $r_2$ , respectively. Show that the electric field due to the charge is

$\begin{array}{ll}\vec{\mathbf{E}}=\vec{\mathbf{0}}&(r\leqr_1);\\\vec{\mathbf{E}}=\frac{Q}{4\pi\epsilon_0r^2}\left(\frac{r^3-r_1^3}{r_2^3-r_1^3}\right)\hat{\mathbf{r}}&(r_1\leq r\leq r_2);\\\vec{\mathbf{E}}=\frac{Q}{4\pi\epsilon_0r^2}\hat{\mathbf{r}}&(r\geq r_2).\end{array}$

47. When a charge is placed on a metal sphere, it ends up in equilibrium at the outer surface. Use this information to determine the electric field of $+3.0~\mu\mathrm{C}$ charge put on a $5.0{\text -}\mathrm{cm}$ aluminum spherical ball at the following two points in space: (a) a point $1.0~\mathrm{cm}$ from the centre of the ball (an inside point) and (b) a point $10~\mathrm{cm}$ from the centre of the ball (an outside point).

48. A large sheet of charge has a uniform charge density of $10~\mu\mathrm{C/m}^2$ . What is the electric field due to this charge at a point just above the surface of the sheet?

49. Determine if approximate cylindrical symmetry holds for the following situations. State why or why not. (a) A $300{\text -}\mathrm{cm}$ long copper rod of radius $1~\mathrm{cm}$ is charged with $+500~\mathrm{nC}$ of charge and we seek electric field at a point $5~\mathrm{cm}$ from the centre of the rod. (b) A $10{\text -}\mathrm{cm}$ long copper rod of radius $1~\mathrm{cm}$ is charged with $+500~\mathrm{nC}$ of charge and we seek electric field at a point $5~\mathrm{cm}$ from the centre of the rod. (c) A $150{\text -}\mathrm{cm}$ wooden rod is glued to a $150{\text -}\mathrm{cm}$ plastic rod to make a $300{\text -}\mathrm{cm}$ long rod, which is then painted with a charged paint so that one obtains a uniform charge density. The radius of each rod is $1~\mathrm{cm}$ , and we seek an electric field at a point that is $4~\mathrm{cm}$ from the centre of the rod. (d) Same rod as (c), but we seek electric field at a point that is $500~\mathrm{cm}$ from the centre of the rod.

50. A long silver rod of radius $3~\mathrm{cm}$ has a charge of $-5~\mu\mathrm{C/cm}$ on its surface. (a) Find the electric field at a point $5~\mathrm{cm}$ from the centre of the rod (an outside point). (b) Find the electric field at a point $2~\mathrm{cm}$ from the centre of the rod (an inside point).

51. The electric field at $2~\mathrm{cm}$ from the centre of long copper rod of radius $1~\mathrm{cm}$ has a magnitude $3~\mathrm{N/C}$ and directed outward from the axis of the rod. (a) How much charge per unit length exists on the copper rod? (b) What would be the electric flux through a cube of side $5~\mathrm{cm}$ situated such that the rod passes through opposite sides of the cube perpendicularly?

52. A long copper cylindrical shell of inner radius $2~\mathrm{cm}$ and outer radius $3~\mathrm{cm}$ surrounds concentrically a charged long aluminum rod of radius $1~\mathrm{cm}$ with a charge density of $4~\mathrm{pC/m}$ . All charges on the aluminum rod reside at its surface. The inner surface of the copper shell has exactly opposite charge to that of the aluminum rod while the outer surface of the copper shell has the same charge as the aluminum rod. Find the magnitude and direction of the electric field at points that are at the following distances from the centre of the aluminum rod: (a) $0.5~\mathrm{cm}$ , (b) $1.5~\mathrm{cm}$ , (c) $2.5~\mathrm{cm}$ , (d) $3.5~\mathrm{cm}$ , and (e) $7\mathrm{cm}$ .

53. Charge is distributed uniformly with a density $\rho$ throughout an infinitely long cylindrical volume of radius $R$ . Show that the field of this charge distribution is directed radially with respect to the cylinder and that

$\begin{array}{ll}E=\frac{\rho r}{2\epsilon_0}&(r\leq R);\\~&~\\E=\frac{\rho R^2}{2\epsilon_0r}&(r\geq R).\end{array}$

54. Charge is distributed throughout a very long cylindrical volume of radius $R$ such that the charge density increases with the distance $r$ from the central axis of the cylinder according to $\rho=\alpha r$ , where $\alpha$ is a constant. Show that the field of this charge distribution is directed radially with respect to the cylinder and that

$\begin{array}{ll}E=\frac{\alpha r^2}{2\epsilon_0}&(r\leq R);\\~&~\\E=\frac{\alpha R^3}{3\epsilon_0r}&(r\geq R).\end{array}$

55. The electric field $10.0~\mathrm{cm}$ from the surface of a copper ball of radius $5.0~\mathrm{cm}$ is directed toward the ball’s centre and has magnitude $4.0\times10^2~\mathrm{N/C}$ . How much charge is on the surface of the ball?

56. Charge is distributed throughout a spherical shell of inner radius $r_1$ and outer radius $r_2$ with a volume density given by $\rho=\rho_0r_1/r$ , where $\rho_0$ is a constant. Determine the electric field due to this charge as a function of $r$ , the distance from the centre of the shell.

57. Charge is distributed throughout a spherical volume of radius $R$ with a density $\rho=\alpha r^2$ , where $\alpha$ is a constant. Determine the electric field due to the charge at points both inside and outside the sphere.

58. Consider a uranium nucleus to be sphere of radius $R=7.4\times10^{-15}~\mathrm{m}$ with a charge of $92e$ distributed uniformly throughout its volume. (a) What is the electric force exerted on an electron when it is $3.0\times10^{-15}~\mathrm{m}$ from the centre of the nucleus? (b) What is the acceleration of the electron at this point?

59. The volume charge density of a spherical charge distribution is given by $\rho(r)=\rho_0e^{-\alpha r}$ , where $\rho_0$ and $\alpha$ are constants. What is the electric field produced by this charge distribution?

2.4 Conductors in Electrostatic Equilibrium

60. An uncharged conductor with an internal cavity is shown in the following figure. Use the closed surface $S$ along with Gauss’ law to show that when a charge $q$ is placed in the cavity a total charge $-q$ is induced on the inner surface of the conductor. What is the charge on the outer surface of the conductor?

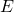A metal sphere with a cavity is shown. It is labeled vector E equal to zero. There are plus signs surrounding it. There is a positive charge labeled plus q within the cavity. The cavity is surrounded by minus signs. — **Figure 2.5.1** A charge inside a cavity of a metal. Charges at the outer surface do not depend on how the charges are distributed at the inner surface since $E$ field inside the body of the metal is zero.

61. An uncharged spherical conductor $S$ of radius $R$ has two spherical cavities $\mathrm{A}$ and $\mathrm{B}$ of radii $a$ and $b$ , respectively as shown below. Two point charges $+q_a$ and $+q_b$ are placed at the centre of the two cavities by using non-conducting supports. In addition, a point charge $+q_0$ is placed outside at a distance $r$ from the centre of the sphere. (a) Draw approximate charge distributions in the metal although metal sphere has no net charge. (b) Draw electric field lines. Draw enough lines to represent all distinctly different places.
Figure shows a sphere with two cavities. A positive charge qa is in one cavity and a positive charge qb is in the other cavity. A positive charge q0 is outside the sphere at a distance r from its center.

62. A positive point charge is placed at the angle bisector of two uncharged plane conductors that make an angle of $45^{\circ}$ . See below. Draw the electric field lines.
An acute angle is shown. Its bisector is a dotted line. A positive charge q is shown on the dotted line.

63. A long cylinder of copper of radius $3~\mathrm{cm}$ is charged so that it has a uniform charge per unit length on its surface of $3~\mathrm{C/m}$ . (a) Find the electric field inside and outside the cylinder. (b) Draw electric field lines in a plane perpendicular to the rod.

64. An aluminum spherical ball of radius $4~\mathrm{cm}$ is charged with $5~\mu\mathrm{C}$ of charge. A copper spherical shell of inner radius $6~\mathrm{cm}$ and outer radius $8~\mathrm{cm}$ surrounds it. A total charge of $-8~\mu\mathrm{C}$ is put on the copper shell. (a) Find the electric field at all points in space, including points inside the aluminum and copper shell when copper shell and aluminum sphere are concentric. (b) Find the electric field at all points in space, including points inside the aluminum and copper shell when the centres of copper shell and aluminum sphere are $1~\mathrm{cm}$ apart.

65. A long cylinder of aluminum of radius $R$ meters is charged so that it has a uniform charge per unit length on its surface of $\lambda$ . (a) Find the electric field inside and outside the cylinder. (b) Plot electric field as a function of distance from the centre of the rod.

66. At the surface of any conductor in electrostatic equilibrium, $E=\sigma/\epsilon_0$ . Show that this equation is consistent with the fact that $E=kq/r^2$ at the surface of a spherical conductor.

67. Two parallel plates $10~\mathrm{cm}$ on a side are given equal and opposite charges of magnitude $5.0\times10^{-9}~\mathrm{C}$ . The plates are $1.5~\mathrm{mm}$ apart. What is the electric field at the centre of the region between the plates?

68. Two parallel conducting plates, each of cross-sectional area $400~\mathrm{cm}^2$ , are $2.0~\mathrm{cm}$ apart and uncharged. If $1.0\times10^{12}$ electrons are transferred from one plate to the other, what are (a) the charge density on each plate? (b) The electric field between the plates?

69. The surface charge density on a long straight metallic pipe is $\sigma$ . What is the electric field outside and inside the pipe? Assume the pipe has a diameter of $2a$ .

Figure shows a pipe, with a cylindrical section highlighted. An arrow pointing up and one pointing down along the pipe from the cylinder are labeled infinity. There are plus signs inside the walls of the cylinder.

70. A point charge $q=-5.0\times10^{-12}~\mathrm{C}$ is placed at the centre of a spherical conducting shell of inner radius $3.5~\mathrm{cm}$ and outer radius $4.0~\mathrm{cm}$ . The electric field just above the surface of the conductor is directed radially outward and has magnitude $8.0~\mathrm{N/C}$ . (a) What is the charge density on the inner surface of the shell? (b) What is the charge density on the outer surface of the shell? (c) What is the net charge on the conductor?

71. A solid cylindrical conductor of radius $a$ is surrounded by a concentric cylindrical shell of inner radius $b$ . The solid cylinder and the shell carry charges $+Q$ and $-Q$ , respectively. Assuming that the length $L$ of both conductors is much greater than $a$ or $b$ , determine the electric field as a function of $r$ , the distance from the common central axis of the cylinders, for (a) $r<a$ ; (b) $a<r<b$ ; and (c) $r>b$ .

Additional Problems

72. A vector field $\vec{\mathbf{E}}$ (not necessarily an electric field; note units) is given by $\vec{\mathbf{E}}=3x^2\hat{\mathbf{k}}$ . Calculate $\int_S\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}da$ , where $S$ is the area shown below. Assume that $\hat{\mathbf{n}}=\hat{\mathbf{k}}$ .
A square S with length of each side equal to a is shown in the xy plane.

A square S with length of each side equal to a is shown in the xy plane.

73. Repeat the preceding problem, with $\vec{\mathbf{E}}=2x\hat{\mathbf{i}}+3x^2\hat{\mathbf{k}}$ .

74. A circular area $S$ is concentric with the origin, has radius $a$ , and lies in the $yz$ -plane. Calculate $\int_S\vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA$ for $\vec{\mathbf{E}}=3z^2\hat{\mathbf{i}}$ .

75. (a) Calculate the electric flux through the open hemispherical surface due to the electric field $\vec{\mathbf{E}}=E_0\hat{\mathbf{k}}$ (see below). (b) If the hemisphere is rotated by $90^{\circ}$ around the $x$ -axis, what is the flux through it?

A hemisphere with radius R is shown with its base in the xy plane and center of base at the origin. An arrow is shown beside it, labeled vector E equal to E0 k hat.

76. Suppose that the electric field of an isolated point charge were proportional to $1/r^{2+\sigma}$ rather than $1/r^2$ . Determine the flux that passes through the surface of a sphere of radius $R$ centred at the charge. Would Gauss’s law remain valid?

77. The electric field in a region is given by $\vec{\mathbf{E}}=a/(b+cx)\hat{\mathbf{i}}$ where $a=200~\mathrm{N}\cdot\mathrm{m/C}$ , $b=2.00~\mathrm{m}$ and $c=2.0$ . What is the net charge enclosed by the shaded volume shown below?

Figure shows a cuboid with one corner on the origin of the coordinate axes. Its length along the x axis is 2 m, along y axis is 1.5 m and along z axis is 1 m. An arrow outside the cuboid points along the x axis. It is labeled vector E.

78. Two equal and opposite charges of magnitude $Q$ are located on the x-axis at the points $+a$ and $-a$ , as shown below. What is the net flux due to these charges through a square surface of side $2a$ that lies in the $yz$ -plane and is centred at the origin? (Hint:Determine the flux due to each charge separately, then use the principle of superposition. You may be able to make a symmetry argument.)
A shaded square is shown in the yz plane with its center at the origin. Its side parallel to z axis is labeled to be of length 2a. A charge labeled plus Q is shown on the positive x axis at a distance a from the origin. A charge labeled minus Q is shown on the negative x axis at a distance a from the origin.

79. A fellow student calculated the flux through the square for the system in the preceding problem and got $0$ . What went wrong?

80. A $10~\mathrm{cm}\times10~\mathrm{cm}$ piece of aluminum foil of $0.1~\mathrm{mm}$ thickness has a charge of $20~\mu\mathrm{C}$ that spreads on both wide side surfaces evenly. You may ignore the charges on the thin sides of the edges. (a) Find the charge density. (b) Find the electric field $1~\mathrm{cm}$ from the centre, assuming approximate planar symmetry.

81. Two $10~\mathrm{cm}\times10~\mathrm{cm}$ pieces of aluminum foil of thickness $0.1~\mathrm{mm}$ face each other with a separation of $5~\mathrm{mm}$ . One of the foils has a charge of $+30~\mu\mathrm{C}$ and the other has $-30~\mu\mathrm{C}$ . (a) Find the charge density at all surfaces, i.e., on those facing each other and those facing away. (b) Find the electric field between the plates near the center assuming planar symmetry.

82. Two large copper plates facing each other have charge densities $\pm4.0~\mathrm{C/m}^2$ on the surface facing the other plate, and zero in between the plates. Find the electric flux through a $3~\mathrm{cm}\times4~\mathrm{cm}$ rectangular area between the plates, as shown below, for the following orientations of the area. (a) If the area is parallel to the plates, and (b) if the area is tilted $\theta=30^{\circ}$ from the parallel direction. Note, this angle can also be $\theta=180^{\circ}+30^{\circ}$ .

Figure shows two parallel plates and a dotted line exactly between the two, parallel to them. A third plate forms an angle theta with the dotted line.

83. The infinite slab between the planes defined by $z=-a/2$ and $z=a/2$ contains a uniform volume charge density $\rho$ (see below). What is the electric field produced by this charge distribution, both inside and outside the distribution?

84. A total charge $Q$ is distributed uniformly throughout a spherical volume that is centred at $O_1$ and has a radius $R$ . Without disturbing the charge remaining, charge is removed from the spherical volume that is centred at $O_2$ (see below). Show that the electric field everywhere in the empty region is given by $\vec{\mathbf{E}}=\frac{Q\vec{\mathbf{r}}}{4\pi\epsilon_0R^3}$ where $\vec{\mathbf{r}}$ is the displacement vector directed from $O_1$ to $O_2$ .

Figure shows a circle with center O1 and radius R. Another smaller circle with center O2 is shown within it. An arrow from O1 to O2 is labeled vector r.

85. A non-conducting spherical shell of inner radius $a_1$ and outer radius $b_1$ is uniformly charged with charged density $\rho_1$ inside another non-conducting spherical shell of inner radius $a_2$ and outer radius $b_2$ that is also uniformly charged with charge density $\rho_2$ . See below. Find the electric field at space point $P$ at a distance $r$ from the common centre such that (a) $r>b_2$ , (b) $a_2<r<b_2$ , (c) $b_1<r<a_2$ , (d) $a_1<r<b_1$ , and (e) $r<a_1$ .
Figure shows two concentric circular shells. The inner and outer radii of the inner shell are a1 and a2 respectively. The inner and outer radii of the outer shell are a2 and b2 respectively. The distance from the center to a point P between the two shells is labeled r.

Figure shows two concentric circular shells. The inner and outer radii of the inner shell are a1 and a2 respectively. The inner and outer radii of the outer shell are a2 and b2 respectively. The distance from the center to a point P between the two shells is labeled r.

86. Two non-conducting spheres of radii $R_1$ and $R_2$ are uniformly charged with charge densities $\rho_1$ and $\rho_2$ , respectively. They are separated at centre-to-centre distance $a$ (see below). Find the electric field at point $P$ located at a distance $r$ from the centre of sphere $1$ and is in the direction $\theta$ from the line joining the two spheres assuming their charge densities are not affected by the presence of the other sphere. (Hint: Work one sphere at a time and use the superposition principle.)
Two circles are shown side by side with the distance between their centers being a. The bigger circle has radius R1 and the smaller one has radius R2. An arrow r is shown from the center of the bigger circle to a point P outside the circles. r forms an angle theta with a.

Two circles are shown side by side with the distance between their centers being a. The bigger circle has radius R1 and the smaller one has radius R2. An arrow r is shown from the center of the bigger circle to a point P outside the circles. r forms an angle theta with a.

87. A disk of radius $R$ is cut in a non-conducting large plate that is uniformly charged with charge density $\sigma$ (coulomb per square meter). See below. Find the electric field at a height $h$ above the centre of the disk. $(h\gg R,\ h\ll l\ \mathrm{or}\ w)$ . (Hint: Fill the hole with $\pm\sigma$ .)
A plate with length l and width w has a hole in the center. A point P above the plate is at a distance h from its center.

A plate with length l and width w has a hole in the center. A point P above the plate is at a distance h from its center.

88. Concentric conducting spherical shells carry charges $Q$ and $-Q$ , respectively (see below). The inner shell has negligible thickness. Determine the electric field for (a) $r<a$ ; (b) $a<r<b$ ; (c) $b<r<c$ ; and (d) $r>c$ .
Section of two concentric spherical shells is shown. The inner shell has a radius a. It is labeled Q and has plus signs around it. The outer shell has an inner radius b and an outer radius c. It is labeled minus Q and has minus signs around it.

Section of two concentric spherical shells is shown. The inner shell has a radius a. It is labeled Q and has plus signs around it. The outer shell has an inner radius b and an outer radius c. It is labeled minus Q and has minus signs around it.

89. Shown below are two concentric conducting spherical shells of radii $R_1$ and $R_2$ , each of finite thickness much less than either radius. The inner and outer shell carry net charges $q_1$ and $q_2$ respectively, where both $q_1$ and $q_2$ are positive. What is the electric field for (a) $r<R_1$ ; (b) $R_1<r<R_2$ ; and (c) $r>R_2$ ? (d) What is the net charge on the inner surface of the inner shell, the outer surface of the inner shell, the inner surface of the outer shell, and the outer surface of the outer shell?
Figure shows section of two concentric spherical shells. The inner one has radius R1 and the outer one has radius R2.

Figure shows section of two concentric spherical shells. The inner one has radius R1 and the outer one has radius R2.

90. A point charge of $q=5.0\times10^{-8}~\mathrm{C}$ is placed at the centre of an uncharged spherical conducting shell of inner radius $6.0~\mathrm{cm}$ and outer radius $9.0~\mathrm{cm}$ . Find the electric field at (a) $r=4.0~\mathrm{cm}$ , (b) $r=8.0~\mathrm{cm}$ , and (c) $r=12.0~\mathrm{cm}$ . (d) What are the charges induced on the inner and outer surfaces of the shell?

Challenge Problems

91. The Hubble Space Telescope can measure the energy flux from distant objects such as supernovae and stars. Scientists then use this data to calculate the energy emitted by that object. Choose an interstellar object which scientists have observed the flux at the Hubble with (e.g. Vega), find (e.g. through an internet search) the distance to that object and the size of Hubble’s primary mirror, and calculate the total energy flux. (Hint: The Hubble intercepts only a small part of the total flux.)

92. Re-derive Gauss’s law for the gravitational field, with $\vec{\mathbf{g}}$ directed positively outward.

93. An infinite plate sheet of charge of surface charge density $\sigma$ is shown below. What is the electric field at a distance $x$ from the sheet? Compare the result of this calculation with that of worked out in the text.

Figure shows a plane with plus signs on it. It goes through a cylinder S perpendicularly at the center, dividing the cylinder into two halves of length x each. The top surface of the cylinder is labeled A. Arrows labeled E emerge from both ends of the cylinder, along its axis.

94. A spherical rubber balloon carries a total charge $Q$ distributed uniformly over its surface. At $t=0$ , the radius of the balloon is $R$ . The balloon is then slowly inflated until its radius reaches $2R$ at the time $t_0$ . Determine the electric field due to this charge as a function of time (a) at the surface of the balloon, (b) at the surface of radius $R$ , and (c) at the surface of radius $2R$ . Ignore any effect on the electric field due to the material of the balloon and assume that the radius increases uniformly with time.

95. Find the electric field of a large conducting plate containing a net charge $q$ . Let $A$ be area of one side of the plate and $h$ the thickness of the plate (see below). The charge on the metal plate will distribute mostly on the two planar sides and very little on the edges if the plate is thin.

A cylinder goes through a hole at the center of a plate of thickness h. The plate has plus signs on its edge. The cylinder is labeled Gaussian pill box. The portion of the cylinder on the right side of the plate is of length z. Two arrows from its flat surface point outward, perpendicular to the surface. These are labeled vector E subscript P and delta vector A. The flat surface of the cylinder to the left of the plate has two arrows perpendicular to it, pointing outward. These are labeled mod vector E equal to mod vector E subscript P and delta vector A.

License

Icon for the Creative Commons Attribution 4.0 International License