Chapter 6 Review

Samuel J. Ling; Jeff Sanny; William Moebs; Daryl Janzen

Chapter 6 Review

Key Terms

ammeter
instrument that measures current

electromotive force (emf)
energy produced per unit charge, drawn from a source that produces an electrical current

equivalent resistance
resistance of a combination of resistors; it can be thought of as the resistance of a single resistor that can replace a combination of resistors in a series and/or parallel circuit

internal resistance
amount of resistance to the flow of current within the voltage source

junction rule
sum of all currents entering a junction must equal the sum of all currents leaving the junction

Kirchhoff’s rules
set of two rules governing current and changes in potential in an electric circuit

loop rule
algebraic sum of changes in potential around any closed circuit path (loop) must be zero

potential difference
difference in electric potential between two points in an electric circuit, measured in volts

potential drop
loss of electric potential energy as a current travels across a resistor, wire, or other component

RC circuit
circuit that contains both a resistor and a capacitor

shock hazard
hazard in which an electric current passes through a person

terminal voltage
potential difference measured across the terminals of a source when there is no load attached

thermal hazard
hazard in which an excessive electric current causes undesired thermal effects

three-wire system
wiring system used at present for safety reasons, with live, neutral, and ground wires

voltmeter
instrument that measures voltage

Key Equations

Terminal voltage of a single voltage source	$V_{\mathrm{terminal}}=\mathcal{E}-Ir_{\mathrm{eq}}$
Equivalent resistance of a series circuit	$R_{\mathrm{eq}}=R_1+R_2+R_3+\ldots+R_{N-1}+R_N=\sum_{i=1}^NR_i$
Equivalent resistance of a parallel circuit	$R_{\mathrm{eq}}=\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\ldots+\frac{1}{R_{N-1}}+\frac{1}{R_N}\right)^{-1}=\left(\sum_{i=1}^NR_i\right)^{-1}$
Junction rule	$\sum I_\mathrm{in}=\sum I_{\mathrm{out}}$
Loop rule	$\sum V=0$
Terminal voltage of $N$ voltage sources in series	$V_{\mathrm{terminal}}=\sum_{i=1}^N\mathcal{E}_i-I\sum_{i=1}^NR_i=\sum_{i=1}^N\mathcal{E}_i-IR_{\mathrm{eq}}$
Terminal voltage of $N$ voltage sources in parallel	$V_{\mathrm{terminal}}=\mathcal{E}-I\sum_{i=1}^N\left(\frac{1}{R_i}\right)^{-1}=\mathcal{E}-IR_{\mathrm{eq}}$
Charge on a charging capacitor	$q(t)=C\mathcal{E}\left(1-e^{-\frac{t}{RC}}\right)=Q\left(1-e^{-\frac{t}{\tau}}\right)$
Time constant	$\tau=RC$
Current during charging of a capacitor	$I=\frac{\mathcal{E}}{R}e^{-\frac{t}{RC}}=I_0e^{-\frac{t}{\tau}}$
Charge on a discharging capacitor	$q(t)=Qe^{-\frac{t}{\tau}}$
Current during discharging of a capacitor	$I(t)=-\frac{Q}{RC}e^{-\frac{t}{\tau}}$

Summary

6.1 Electromotive Force

All voltage sources have two fundamental parts: a source of electrical energy that has a characteristic electromotive force (emf), and an internal resistance $r$ . The emf is the work done per charge to keep the potential difference of a source constant. The emf is equal to the potential difference across the terminals when no current is flowing. The internal resistance $r$ of a voltage source affects the output voltage when a current flows.
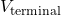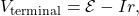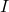The voltage output of a device is called its terminal voltage $V_{\mathrm{terminal}}$ and is given by $V_{\mathrm{terminal}}=\mathcal{E}-Ir,$ where $I$ is the electric current and is positive when flowing away from the positive terminal of the voltage source and $r$ is the internal resistance.

6.2 Resistors in Series and Parallel

The equivalent resistance of an electrical circuit with resistors wired in a series is the sum of the individual resistances: $R_{\mathrm{eq}}=R_1+R_2+R_3+\ldots+R_{N-1}+R_N=\sum_{i=1}^NR_i$ .
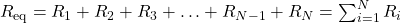Each resistor in a series circuit has the same amount of current flowing through it.
The potential drop, or power dissipation, across each individual resistor in a series is different, and their combined total is the power source input.
The equivalent resistance of an electrical circuit with resistors wired in parallel is less than the lowest resistance of any of the components and can be determined using the formula $R_{\mathrm{eq}}=\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\ldots+\frac{1}{R_{N-1}}+\frac{1}{R_N}\right)^{-1}=\left(\sum_{i=1}^NR_i\right)^{-1}$ .
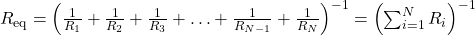Each resistor in a parallel circuit has the same full voltage of the source applied to it.
The current flowing through each resistor in a parallel circuit is different, depending on the resistance.
If a more complex connection of resistors is a combination of series and parallel, it can be reduced to a single equivalent resistance by identifying its various parts as series or parallel, reducing each to its equivalent, and continuing until a single resistance is eventually reached.

6.3 Kirchhoff’s Rules

Kirchhoff’s rules can be used to analyze any circuit, simple or complex. The simpler series and parallel connection rules are special cases of Kirchhoff’s rules.
Kirchhoff’s first rule, also known as the junction rule, applies to the charge to a junction. Current is the flow of charge; thus, whatever charge flows into the junction must flow out.
Kirchhoff’s second rule, also known as the loop rule, states that the voltage drop around a loop is zero.
When calculating potential and current using Kirchhoff’s rules, a set of conventions must be followed for determining the correct signs of various terms.
When multiple voltage sources are in series, their internal resistances add together and their emfs add together to get the total values.
When multiple voltage sources are in parallel, their internal resistances combine to an equivalent resistance that is less than the individual resistance and provides a higher current than a single cell.
Solar cells can be wired in series or parallel to provide increased voltage or current, respectively.

6.4 Electrical Measuring Instruments

Voltmeters measure voltage, and ammeters measure current. Analog meters are based on the combination of a resistor and a galvanometer, a device that gives an analog reading of current or voltage. Digital meters are based on analog-to-digital converters and provide a discrete or digital measurement of the current or voltage.
A voltmeter is placed in parallel with the voltage source to receive full voltage and must have a large resistance to limit its effect on the circuit.
An ammeter is placed in series to get the full current flowing through a branch and must have a small resistance to limit its effect on the circuit.
Standard voltmeters and ammeters alter the circuit they are connected to and are thus limited in accuracy.
Ohmmeters are used to measure resistance. The component in which the resistance is to be measured should be isolated (removed) from the circuit.

6.5 RC Circuits

An 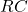$RC$ circuit is one that has both a resistor and a capacitor.
The time constant 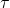$\tau$ for an 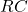$RC$ circuit is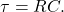 $\tau=RC.$
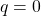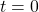When an initially uncharged ( $q=0$ at $t=0$ ) capacitor in series with a resistor is charged by a dc voltage source, the capacitor asymptotically approaches the maximum charge.
As the charge on the capacitor increases, the current exponentially decreases from the initial current: $I_0=\mathcal{E}/R.$
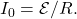
If a capacitor with an initial charge $Q$ is discharged through a resistor starting at 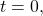$t=0,$ then its charge decreases exponentially. The current flows in the opposite direction, compared to when it charges, and the magnitude of the charge decreases with time.

6.6 Household Wiring and Electrical Safety

The two types of electric hazards are thermal (excessive power) and shock (current through a person). Electrical safety systems and devices are employed to prevent thermal and shock hazards.
Shock severity is determined by current, path, duration, and ac frequency.
Circuit breakers and fuses interrupt excessive currents to prevent thermal hazards.
The three-wire system guards against thermal and shock hazards, utilizing live/hot, neutral, and ground wires, and grounding the neutral wire and case of the appliance.
A ground fault circuit interrupter (GFCI) prevents shock by detecting the loss of current to unintentional paths.

Answers to Check Your Understanding

6.1 If a wire is connected across the terminals, the load resistance is close to zero, or at least considerably less than the internal resistance of the battery. Since the internal resistance is small, the current through the circuit will be large, $I=\frac{\mathcal{E}}{R+r}=\frac{\mathcal{E}}{0+r}=\frac{\mathcal{E}}{r}.$ The large current causes a high power to be dissipated by the internal resistance ( $P=I^2r$ ). The power is dissipated as heat.

6.2 The equivalent resistance of nine bulbs connected in series is $9R.$ The current is $I=V/9R.$ If one bulb burns out, the equivalent resistance is $8R,$ and the voltage does not change, but the current increases ( $I=V/8R$ ) As more bulbs burn out, the current becomes even higher. Eventually, the current becomes too high, burning out the shunt.

6.3 The equivalent of the series circuit would be $R_{\mathrm{eq}}=1.00~\Omega+2.00~\Omega+2.00~\Omega=5.00~\Omega,$ which is higher than the equivalent resistance of the parallel circuit $R_{\mathrm{eq}}=0.50~\Omega.$ The equivalent resistor of any number of resistors is always higher than the equivalent resistance of the same resistors connected in parallel. The current through for the series circuit would be $I=\frac{3.00~\mathrm{V}}{5.00~\Omega}=0.60~\mathrm{A},$ which is lower than the sum of the currents through each resistor in the parallel circuit, $I=6.00~\mathrm{A}.$ This is not surprising since the equivalent resistance of the series circuit is higher. The current through a series connection of any number of resistors will always be lower than the current into a parallel connection of the same resistors, since the equivalent resistance of the series circuit will be higher than the parallel circuit. The power dissipated by the resistors in series would be $P=1.80~\mathrm{W},$ which is lower than the power dissipated in the parallel circuit $P=18.00~\mathrm{W}.$

6.4 A river, flowing horizontally at a constant rate, splits in two and flows over two waterfalls. The water molecules are analogous to the electrons in the parallel circuits. The number of water molecules that flow in the river and falls must be equal to the number of molecules that flow over each waterfall, just like sum of the current through each resistor must be equal to the current flowing into the parallel circuit. The water molecules in the river have energy due to their motion and height. The potential energy of the water molecules in the river is constant due to their equal heights. This is analogous to the constant change in voltage across a parallel circuit. Voltage is the potential energy across each resistor.

The analogy quickly breaks down when considering the energy. In the waterfall, the potential energy is converted into kinetic energy of the water molecules. In the case of electrons flowing through a resistor, the potential drop is converted into heat and light, not into the kinetic energy of the electrons.

6.5 1. All the overhead lighting circuits are in parallel and connected to the main supply line, so when one bulb burns out, all the overhead lighting does not go dark. Each overhead light will have at least one switch in series with the light, so you can turn it on and off. 2. A refrigerator has a compressor and a light that goes on when the door opens. There is usually only one cord for the refrigerator to plug into the wall. The circuit containing the compressor and the circuit containing the lighting circuit are in parallel, but there is a switch in series with the light. A thermostat controls a switch that is in series with the compressor to control the temperature of the refrigerator.

6.6 The circuit can be analyzed using Kirchhoff’s loop rule. The first voltage source supplies power: $P_{\mathrm{in}}=IV_1=7.20~\mathrm{mW}.$ The second voltage source consumes power: $P_{\mathrm{out}}=IV_2+I^2R_1+I^2R_2=7.2~\mathrm{mW}.$

6.7 The current calculated would be equal to $I=-0.20~\mathrm{A}$ instead of $I=0.20~\mathrm{A}.$ The sum of the power dissipated and the power consumed would still equal the power supplied.

6.8 Since digital meters require less current than analog meters, they alter the circuit less than analog meters. Their resistance as a voltmeter can be far greater than an analog meter, and their resistance as an ammeter can be far less than an analog meter. Consult Figure 6.4.3 and Figure 6.4.2 and their discussion in the text.

Conceptual Questions

6.1 Electromotive Force

1. What effect will the internal resistance of a rechargeable battery have on the energy being used to recharge the battery?

2. A battery with an internal resistance of $r$ and an emf of $10.00~\mathrm{V}$ is connected to a load resistor $R=r.$ As the battery ages, the internal resistance triples. How much is the current through the load resistor reduced?

3. Show that the power dissipated by the load resistor is maximum when the resistance of the load resistor is equal to the internal resistance of the battery.

6.2 Resistors in Series and Parallel

4. A voltage occurs across an open switch. What is the power dissipated by the open switch?

5. The severity of a shock depends on the magnitude of the current through your body. Would you prefer to be in series or in parallel with a resistance, such as the heating element of a toaster, if you were shocked by it? Explain.

6. Suppose you are doing a physics lab that asks you to put a resistor into a circuit, but all the resistors supplied have a larger resistance than the requested value. How would you connect the available resistances to attempt to get the smaller value asked for?

7. Some light bulbs have three power settings (not including zero), obtained from multiple filaments that are individually switched and wired in parallel. What is the minimum number of filaments needed for three power settings?

6.3 Kirchhoff’s Rules

8. Can all of the currents going into the junction shown below be positive? Explain.

The figure shows a junction with three incoming current branches.

9. Consider the circuit shown below. Does the analysis of the circuit require Kirchhoff’s method, or can it be redrawn to simplify the circuit? If it is a circuit of series and parallel connections, what is the equivalent resistance?

The figure shows a circuit with positive terminal of voltage source V connected to three parallel branches. The first branch has resistor R subscript 2 connected to parallel branches with R subscript 4 and R subscript 3 series with R subscript 5. The second branch has resistor R subscript 1 and third branch has resistor R subscript 6.

10. Do batteries in a circuit always supply power to a circuit, or can they absorb power in a circuit? Give an example.

11. What are the advantages and disadvantages of connecting batteries in series? In parallel?

12. Semi-tractor trucks use four large $12{\text -}\mathrm{V}$ batteries. The starter system requires $24~\mathrm{V}$ while normal operation of the truck’s other electrical components utilizes $12~\mathrm{V}.$ How could the four batteries be connected to produce $24~\mathrm{V}$ ? To produce $12~\mathrm{V}$ ? Why is $24~\mathrm{V}$ better than $12~\mathrm{V}$ for starting the truck’s engine (a very heavy load)?

6.4 Electrical Measuring Instruments

13. What would happen if you placed a voltmeter in series with a component to be tested?

14. What is the basic operation of an ohmmeter as it measures a resistor?

15. Why should you not connect an ammeter directly across a voltage source as shown below?

The figure shows positive terminal of a battery with emf ε and internal resistance r connected to ammeter.

6.5 RC Circuits

16. A battery, switch, capacitor, and lamp are connected in series. Describe what happens to the lamp when the switch is closed.

17. When making an ECG measurement, it is important to measure voltage variations over small time intervals. The time is limited by the $RC$ constant of the circuit—it is not possible to measure time variations shorter than $RC.$ How would you manipulate $R$ and $C$ in the circuit to allow the necessary measurements?

6.6 Household Wiring and Electrical Safety

18. Why isn’t a short circuit necessarily a shock hazard?

19. We are often advised to not flick electric switches with wet hands, dry your hand first. We are also advised to never throw water on an electric fire. Why?

Problems

6.1 Electromotive Force

20. A car battery with a $12{\text -}\mathrm{V}$ emf and an internal resistance of $0.050~\Omega$ is being charged with a current of $60~\mathrm{A}.$ Note that in this process, the battery is being charged. (a) What is the potential difference across its terminals? (b) At what rate is thermal energy being dissipated in the battery? (c) At what rate is electric energy being converted into chemical energy?

21. The label on a battery-powered radio recommends the use of rechargeable nickel-cadmium cells (nicads), although they have a $1.25{\text -}\mathrm{V}$ emf, whereas alkaline cells have a $1.58{\text -}\mathrm{V}$ emf. The radio has a $3.20~\Omega$ resistance. (a) Draw a circuit diagram of the radio and its batteries. Now, calculate the power delivered to the radio (b) when using nicad cells, each having an internal resistance of $0.0400~\Omega,$ and (c) when using alkaline cells, each having an internal resistance of $0.200~\Omega.$ (d) Does this difference seem significant, considering that the radio’s effective resistance is lowered when its volume is turned up?

22. An automobile starter motor has an equivalent resistance of $0.0500~\Omega$ and is supplied by a $12.0{\text -}\mathrm{V}$ battery with a $0.0100{\text -}\Omega$ internal resistance. (a) What is the current to the motor? (b) What voltage is applied to it? (c) What power is supplied to the motor? (d) Repeat these calculations for when the battery connections are corroded and add $0.0900~\Omega$ to the circuit. (Significant problems are caused by even small amounts of unwanted resistance in low-voltage, high-current applications.)

23. (a) What is the internal resistance of a voltage source if its terminal potential drops by $2.00~\mathrm{V}$ when the current supplied increases by $5.00~\mathrm{A}$ ? (b) Can the emf of the voltage source be found with the information supplied?

24. A person with body resistance between his hands of $10.0~\mathrm{k}\Omega$ accidentally grasps the terminals of a $20.0{\text -}\mathrm{kV}$ power supply. (Do NOT do this!) (a) Draw a circuit diagram to represent the situation. (b) If the internal resistance of the power supply is $2000~\Omega,$ what is the current through his body? (c) What is the power dissipated in his body? (d) If the power supply is to be made safe by increasing its internal resistance, what should the internal resistance be for the maximum current in this situation to be $1.00~\mathrm{mA}$ or less? (e) Will this modification compromise the effectiveness of the power supply for driving low-resistance devices? Explain your reasoning.

25. A $12.0{\text -}\mathrm{V}$ emf automobile battery has a terminal voltage of $16.0~\mathrm{V}$ when being charged by a current of $10.0~\mathrm{A}.$ (a) What is the battery’s internal resistance? (b) What power is dissipated inside the battery? (c) At what rate (in $^{\circ}\mathrm{C/min}$ ) will its temperature increase if its mass is $20.0~\mathrm{kg}$ and it has a specific heat of $0.300~\mathrm{kcal/kg}\cdot^{\circ}\mathrm{C},$ assuming no heat escapes?

6.2 Resistors in Series and Parallel

26. (a) What is the resistance of a $1.00\times10^2{\text -}\Omega,$ a $2.50{\text -}\mathrm{k}\Omega,$ and a $4.00{\text -}\mathrm{k}\Omega$ resistor connected in series? (b) In parallel?

27. What are the largest and smallest resistances you can obtain by connecting a $36.0{\text -}\Omega,$ a $50.0{\text -}\Omega,$ and a $700{\text -}\Omega$ resistor together?

28. An $1800{\text -}\mathrm{W}$ toaster, a $1400{\text -}\mathrm{W}$ speaker, and a $75{\text -}\mathrm{W}$ lamp are plugged into the same outlet in a $15{\text -}\mathrm{A}$ fuse and $120{\text -}\mathrm{V}$ circuit. (The three devices are in parallel when plugged into the same socket.) (a) What current is drawn by each device? (b) Will this combination blow the $15{\text -}\mathrm{A}$ fuse?

29. Your car’s $30.0{\text -}\mathrm{W}$ headlight and $2.40{\text -}\mathrm{kW}$ starter are ordinarily connected in parallel in a $12.0{\text -}\mathrm{V}$ system. What power would one headlight and the starter consume if connected in series to a $12.0{\text -}\mathrm{V}$ battery? (Neglect any other resistance in the circuit and any change in resistance in the two devices.)

30. (a) Given a $48.0{\text -}\mathrm{V}$ battery and $24.0{\text -}\Omega$ and $96.0{\text -}\Omega$ resistors, find the current and power for each when connected in series. (b) Repeat when the resistances are in parallel.

31. Referring to the example combining series and parallel circuits and Figure 6.2.6, calculate $I_3$ in the following two different ways: (a) from the known values of $I$ and $I_2$ ; (b) using Ohm’s law for $R_3.$ In both parts, explicitly show how you follow the steps in the Figure 6.2.7.

32. Referring to Figure 6.2.6, (a) Calculate $P_3$ and note how it compares with $P_3$ found in the first two example problems in this module. (b) Find the total power supplied by the source and compare it with the sum of the powers dissipated by the resistors.

33. Refer to Figure 6.2.7 and the discussion of lights dimming when a heavy appliance comes on. (a) Given the voltage source is $120~\mathrm{V},$ the wire resistance is $0.800~\Omega,$ and the bulb is nominally $75.0~\mathrm{W},$ what power will the bulb dissipate if a total of $15.0~\mathrm{A}$ passes through the wires when the motor comes on? Assume negligible change in bulb resistance. (b) What power is consumed by the motor?

34. Show that if two resistors $R_1$ and $R_2$ are combined and one is much greater than the other ( $R_1\gg R_2$ ), (a) their series resistance is very nearly equal to the greater resistance $R_1$ and (b) their parallel resistance is very nearly equal to smaller resistance $R_2.$

35. Consider the circuit shown below. The terminal voltage of the battery is $18.00~\mathrm{V}.$ (a) Find the equivalent resistance of the circuit. (b) Find the current through each resistor. (c) Find the potential drop across each resistor. (d) Find the power dissipated by each resistor. (e) Find the power supplied by the battery.

The figure shows negative terminal of a voltage source of 18 V connected to three resistors in series, R subscript 1 of 4 Ω, R subscript 2 of 1 Ω and R subscript 3 of 4 Ω.

6.3 Kirchhoff’s Rules

36. Consider the circuit shown below. (a) Find the voltage across each resistor. (b)What is the power supplied to the circuit and the power dissipated or consumed by the circuit?

37. Consider the circuits shown below. (a) What is the current through each resistor in part (a)? (b) What is the current through each resistor in part (b)? (c) What is the power dissipated or consumed by each circuit? (d) What is the power supplied to each circuit?

38. Consider the circuit shown below. Find $V_1,$ $I_2,$ and $I_3.$

The positive terminal of voltage source V subscript 1 is connected to resistance R subscript 1 of 12 Ω with right current I subscript 1 of 2 A connected to two parallel branches, first with resistor R subscript 2 of 6 Ω with upward current I subscript 2 and second with right current I subscript 3, negative terminal of voltage source V subscript 2 of 21 V and resistor R subscript 3 of 5 Ω.

39. Consider the circuit shown below. Find $V_1,$ $V_2,$ and $R_4.$

40. Consider the circuit shown below. Find $I_1,$ $I_2,$ and $I_3.$

41. Consider the circuit shown below. (a) Find $I_1,$ $I_2,$ $I_3,$ $I_4,$ and $I_5.$ (b) Find the power supplied by the voltage sources. (c) Find the power dissipated by the resistors.

42. Consider the circuit shown below. Write the three loop equations for the loops shown.

43. Consider the circuit shown below. Write equations for the three currents in terms of $R$ and $V.$

44. Consider the circuit shown in the preceding problem. Write equations for the power supplied by the voltage sources and the power dissipated by the resistors in terms of $R$ and $V.$

45. A child’s electronic toy is supplied by three $1.58{\text -}\mathrm{V}$ alkaline cells having internal resistances of $0.0200~\Omega$ in series with a $1.53{\text -}\mathrm{V}$ carbon-zinc dry cell having a $0.100{\text}\Omega$ internal resistance. The load resistance is $10.0~\Omega.$ (a) Draw a circuit diagram of the toy and its batteries. (b) What current flows? (c) How much power is supplied to the load? (d) What is the internal resistance of the dry cell if it goes bad, resulting in only $0.500~\mathrm{W}$ being supplied to the load?

46. Apply the junction rule to Junction $b$ shown below. Is any new information gained by applying the junction rule at $e$ ?

47. Apply the loop rule to Loop $afedcba$ in the preceding problem.

6.4 Electrical Measuring Instruments

48. Suppose you measure the terminal voltage of a $1.585{\text -}\mathrm{V}$ alkaline cell having an internal resistance of $0.100~\Omega$ by placing a $1.00{\text -}\mathrm{k}\Omega$ voltmeter across its terminals (see below). (a) What current flows? (b) Find the terminal voltage. (c) To see how close the measured terminal voltage is to the emf, calculate their ratio.

The figure shows positive terminal of a battery with emf ε and internal resistance r connected to a voltmeter.

6.5 RC Circuits

49. The timing device in an automobile’s intermittent wiper system is based on an $RC$ time constant and utilizes a $0.500{\text -}\mu\mathrm{F}$ capacitor and a variable resistor. Over what range must $R$ be made to vary to achieve time constants from $2.00$ to $15.0~\mathrm{s}$ ?

50. A heart pacemaker fires $72$ times a minute, each time a $25.0{\text -}\mathrm{nF}$ capacitor is charged (by a battery in series with a resistor) to $0.632$ of its full voltage. What is the value of the resistance?

51. The duration of a photographic flash is related to an $RC$ time constant, which is $0.100~\mu\mathrm{F}$ for a certain camera. (a) If the resistance of the flash lamp is $0.0400~\Omega$ during discharge, what is the size of the capacitor supplying its energy? (b) What is the time constant for charging the capacitor, if the charging resistance is $800~\mathrm{k}\Omega$ ?

52. A $2.00$ – and a $7.50{\text -}\mu\mathrm{F}$ capacitor can be connected in series or parallel, as can a $25.0$ – and a $100{\text -}\mathrm{k}\Omega$ resistor. Calculate the four $RC$ time constants possible from connecting the resulting capacitance and resistance in series.

53. A $500{\text -}\Omega$ resistor, an uncharged $1.50{\text -}\mu\mathrm{F}$ capacitor, and a $6.16{\text -}\mathrm{V}$ emf are connected in series. (a) What is the initial current? (b) What is the $RC$ time constant? (c) What is the current after one time constant? (d) What is the voltage on the capacitor after one time constant?

54. A heart defibrillator being used on a patient has an $RC$ time constant of $10.0~\mathrm{ms}$ due to the resistance of the patient and the capacitance of the defibrillator. (a) If the defibrillator has a capacitance of $8.00~\mu\mathrm{F},$ what is the resistance of the path through the patient? (You may neglect the capacitance of the patient and the resistance of the defibrillator.) (b) If the initial voltage is $12.0~\mathrm{kV},$ how long does it take to decline to $6.00\times10^2~\mathrm{V}$ ?

55. An ECG monitor must have an $RC$ time constant less than $1.00\times10^2~\mu\mathrm{s}$ to be able to measure variations in voltage over small time intervals. (a) If the resistance of the circuit (due mostly to that of the patient’s chest) is $1.00~\mathrm{k}\Omega,$ what is the maximum capacitance of the circuit? (b) Would it be difficult in practice to limit the capacitance to less than the value found in (a)?

56. Using the exact exponential treatment, determine how much time is required to charge an initially uncharged $100{\text -}\mathrm{pF}$ capacitor through a $75.0{\text -}\mathrm{M}\Omega$ resistor to $90.0\%$ of its final voltage.

57. If you wish to take a picture of a bullet traveling at $500~\mathrm{m/s},$ then a very brief flash of light produced by an $RC$ discharge through a flash tube can limit blurring. Assuming $1.00~\mathrm{mm}$ of motion during one $RC$ constant is acceptable, and given that the flash is driven by a $600{\text -}\mu\mathrm{F}$ capacitor, what is the resistance in the flash tube?

6.6 Household Wiring and Electrical Safety

58. (a) How much power is dissipated in a short circuit of $240{\text -}\mathrm{V}$ ac through a resistance of $0.250~\Omega$ ? (b) What current flows?

59. What voltage is involved in a $1.44{\text -}\mathrm{kW}$ short circuit through a $0.100{\text -}\Omega$ resistance?

60. Find the current through a person and identify the likely effect on her if she touches a $120{\text -}\mathrm{V}$ ac source: (a) if she is standing on a rubber mat and offers a total resistance of $300~\mathrm{k}\Omega$ ; (b) if she is standing barefoot on wet grass and has a resistance of only $4000~\Omega.$

61. While taking a bath, a person touches the metal case of a radio. The path through the person to the drainpipe and ground has a resistance of $4000~\Omega.$ What is the smallest voltage on the case of the radio that could cause ventricular fibrillation?

62. A man foolishly tries to fish a burning piece of bread from a toaster with a metal butter knife and comes into contact with $120{\text -}\mathrm{V}$ ac. He does not even feel it since, luckily, he is wearing rubber-soled shoes. What is the minimum resistance of the path the current follows through the person?

63. (a) During surgery, a current as small as $20.0~\mu\mathrm{A}$ applied directly to the heart may cause ventricular fibrillation. If the resistance of the exposed heart is $300~\Omega,$ what is the smallest voltage that poses this danger? (b) Does your answer imply that special electrical safety precautions are needed?

64. (a) What is the resistance of a $200{\text -}\mathrm{V}$ ac short circuit that generates a peak power of $96.8~\mathrm{kW}$ ? (b) What would the average power be if the voltage were $120~\mathrm{V}$ ac?

65. A heart defibrillator passes $10.0~\mathrm{A}$ through a patient’s torso for $5.00~\mathrm{ms}$ in an attempt to restore normal beating. (a) How much charge passed? (b) What voltage was applied if $500~\mathrm{J}$ of energy was dissipated? (c) What was the path’s resistance? (d) Find the temperature increase caused in the $8.00~\mathrm{kg}$ of affected tissue.

66. A short circuit in a $120{\text -}\mathrm{V}$ appliance cord has a $0.500{\text -}\Omega$ resistance. Calculate the temperature rise of the $2.00~\mathrm{g}$ of surrounding materials, assuming their specific heat capacity is $0.200~\mathrm{cal/g}\cdot^{\circ}\mathrm{C}$ and that it takes $0.0500~\mathrm{s}$ for a circuit breaker to interrupt the current. Is this likely to be damaging?

Additional Problems

67. A circuit contains a D cell battery, a switch, a $20{\text -}\Omega$ resistor, and four $20{\text -}\mathrm{mF}$ capacitors connected in series. (a) What is the equivalent capacitance of the circuit? (b) What is the $RC$ time constant? (c) How long before the current decreases to $50\%$ of the initial value once the switch is closed?

68. A circuit contains a D-cell battery, a switch, a $20{\text -}\Omega$ resistor, and three $20{\text -}\mathrm{mF}$ capacitors. The capacitors are connected in parallel, and the parallel connection of capacitors are connected in series with the switch, the resistor and the battery. (a) What is the equivalent capacitance of the circuit? (b) What is the $RC$ time constant? (c) How long before the current decreases to $50\%$ of the initial value once the switch is closed?

69. Consider the circuit below. The battery has an emf of $\mathcal{E}=30.00~\mathrm{V}$ and an internal resistance of $r=1.00~\Omega.$ (a) Find the equivalent resistance of the circuit and the current out of the battery. (b) Find the current through each resistor. (c) Find the potential drop across each resistor. (d) Find the power dissipated by each resistor. (e) Find the total power supplied by the batteries.

The figure shows positive terminal of voltage source of 30 V and internal resistance 1 Ω connected in series to two sets of parallel resistors. The first set has R subscript 1 of 9 Ω and R subscript 2 of 18 Ω. The second has R subscript 3 of 10 Ω and R subscript 4 of 10 Ω. The sets are connected in series to resistor R subscript 5 of 8 Ω.

70. A homemade capacitor is constructed of 2 sheets of aluminum foil with an area of $2.00$ square meters, separated by paper, $0.05~\mathrm{mm}$ thick, of the same area and a dielectric constant of $3.7.$ The homemade capacitor is connected in series with a $100.00{\text -}\Omega$ resistor, a switch, and a $6.00{\text -}\mathrm{V}$ voltage source. (a) What is the $RC$ time constant of the circuit? (b) What is the initial current through the circuit, when the switch is closed? (c) How long does it take the current to reach one third of its initial value?

71. A student makes a homemade resistor from a graphite pencil $5.00~\mathrm{cm}$ long, where the graphite is $0.05~\mathrm{mm}$ in diameter. The resistivity of the graphite is $\rho=1.38\times10^{-5}~\Omega/\mathrm{m}.$ The homemade resistor is place in series with a switch, a $10.00{\text -}\mathrm{mF}$ capacitor and a $0.50{\text -}\mathrm{V}$ power source. (a) What is the $RC$ time constant of the circuit? (b) What is the potential drop across the pencil $1.00~\mathrm{s}$ after the switch is closed?

72. The rather simple circuit shown below is known as a voltage divider. The symbol consisting of three horizontal lines is represents “ground” and can be defined as the point where the potential is zero. The voltage divider is widely used in circuits and a single voltage source can be used to provide reduced voltage to a load resistor as shown in the second part of the figure. (a) What is the output voltage $V_{\mathrm{out}}$ of circuit (a) in terms of $R_1,$ $R_2,$ and $V_{\mathrm{in}}$ ? (b) What is the output voltage $V_{\mathrm{out}}$ of circuit (b) in terms of $R_1,$ $R_2,$ $R_L,$ and $V_{\mathrm{in}}$ ?

Part a shows positive terminal of voltage source V subscript in connected in series to resistors R subscript 1 and R subscript 2. The negative terminal of the source is grounded and V subscript out is between the two resistors. Part b shows the same circuit as part a but with V subscript out connected to ground through resistor R subscript L.

73. Three $300{\text -}\Omega$ resistors are connect in series with an AAA battery with a rating of $3$ Amp-hours. (a) How long can the battery supply the resistors with power? (b) If the resistors are connected in parallel, how long can the battery last?

74. Consider a circuit that consists of a real battery with an emf $\mathcal{E}$ and an internal resistance of $r$ connected to a variable resistor $R.$ (a) In order for the terminal voltage of the battery to be equal to the emf of the battery, what should the resistance of the variable resistor be adjusted to? (b) In order to get the maximum current from the battery, what should the resistance variable resistor be adjusted to? (c) In order for the maximum power output of the battery to be reached, what should the resistance of the variable resistor be set to?

75. Consider the circuit shown below. What is the energy stored in each capacitor after the switch has been closed for a very long time?

The positive terminal of voltage source V of 12 V is connected to an open switch. The other end of the open switch is connected to resistor R subscript 1 of 100 Ω which is connected to two parallel branches. The first branch has capacitor C subscript 1 of 10 mF and R subscript 2 of 100 Ω. The second branch has R subscript 3 of 100 Ω and C subscript 2 of 4.7 mF.

76. Consider a circuit consisting of a battery with an emf $\mathcal{E}$ and an internal resistance of $r$ connected in series with a resistor $R$ and a capacitor $C.$ Show that the total energy supplied by the battery while charging the battery is equal to $\mathcal{E}^2C.$

77. Consider the circuit shown below. The terminal voltages of the batteries are shown. (a) Find the equivalent resistance of the circuit and the current out of the battery. (b) Find the current through each resistor. (c) Find the potential drop across each resistor. (d) Find the power dissipated by each resistor. (e) Find the total power supplied by the batteries.

The figure shows two series voltage sources of 12 V each with upward negative terminals connected to four resistors. The sources are connected in series to resistor R subscript 1 of 14 Ω connected in series to two parallel resistors, R subscript 2 of 9 Ω and R subscript 3 of 18 Ω connected in series to resistor R subscript 4 of 4 Ω.

78. Consider the circuit shown below. (a) What is the terminal voltage of the battery? (b) What is the potential drop across resistor $R_2$ ?

The negative terminal of voltage source V is connected to two parallel branches, one with resistor R subscript 1 of 40 Ω with downward current I subscript 1 of 50 mA and second with R subscript 2 of 5 Ω in series with R subscript 3 of 15 Ω.

79. Consider the circuit shown below. (a) Determine the equivalent resistance and the current from the battery with switch $S_1$ open. (b) Determine the equivalent resistance and the current from the battery with switch $S_1$ closed.

The negative terminal of voltage source of 12 V is connected to two parallel branches, one with resistor R subscript 1 of 8 Ω in series with resistor R subscript 4 of 8 Ω and second with R subscript 2 of 8 Ω in series with R subscript 3 of 8 Ω. The branches are connected together to resistor R subscript 5 of 4 Ω. An open switch S connects the two branches in the middle.

80. Two resistors, one having a resistance of $145~\Omega,$ are connected in parallel to produce a total resistance of $150~\Omega.$ (a) What is the value of the second resistance? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

81. Two resistors, one having a resistance of $900~\mathrm{k}\Omega,$ are connected in series to produce a total resistance of $0.500~\mathrm{M}\Omega.$ (a) What is the value of the second resistance? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

82. Apply the junction rule at point $a$ shown below.

83. Apply the loop rule to Loop $akledcba$ in the preceding problem.

84. Find the currents flowing in the circuit in the preceding problem. Explicitly show how you follow the steps in the Problem-Solving Strategy in Resistors in Series and Parallel.

85. Consider the circuit shown below. (a) Find the current through each resistor. (b) Check the calculations by analyzing the power in the circuit.

The positive terminal of voltage source of 20 V and internal resistance 5 Ω is connected to two parallel branches. The first branch has resistors R subscript 1 of 15 Ω and R subscript 3 of 10 Ω. The second branch has resistors R subscript 2 of 10 Ω and R subscript 4 of 15 Ω. The two branches are connected in the middle using resistor R subscript 5 of 5 Ω.

86. A flashing lamp in a Christmas earring is based on an $RC$ discharge of a capacitor through its resistance. The effective duration of the flash is $0.250~\mathrm{s},$ during which it produces an average $0.500~\mathrm{W}$ from an average $3.00~\mathrm{V}.$ (a) What energy does it dissipate? (b) How much charge moves through the lamp? (c) Find the capacitance. (d) What is the resistance of the lamp? (Since average values are given for some quantities, the shape of the pulse profile is not needed.)

87. A $160{\text -}\mu\mathrm{F}$ capacitor charged to $450~\mathrm{V}$ is discharged through a $31.2{\text -}\mathrm{k}\Omega$ resistor. (a) Find the time constant. (b) Calculate the temperature increase of the resistor, given that its mass is $2.50~\mathrm{g}$ and its specific heat is $1.67~\mathrm{kJ/kg}\cdot^{\circ}\mathrm{C},$ noting that most of the thermal energy is retained in the short time of the discharge. (c) Calculate the new resistance, assuming it is pure carbon. (d) Does this change in resistance seem significant?

Challenge Problems

88. Some camera flashes use flash tubes that require a high voltage. They obtain a high voltage by charging capacitors in parallel and then internally changing the connections of the capacitors to place them in series. Consider a circuit that uses four AAA batteries connected in series to charge six $10{\text -}\mathrm{mF}$ capacitors through an equivalent resistance of $100~\Omega.$ The connections are then switched internally to place the capacitors in series. The capacitors discharge through a lamp with a resistance of $100~\Omega.$ (a) What is the $RC$ time constant and the initial current out of the batteries while they are connected in parallel? (b) How long does it take for the capacitors to charge to $90\%$ of the terminal voltages of the batteries? (c) What is the $RC$ time constant and the initial current of the capacitors connected in series assuming it discharges at $90\%$ of full charge? (d) How long does it take the current to decrease to $10\%$ of the initial value?

89. Consider the circuit shown below. Each battery has an emf of $1.50~\mathrm{V}$ and an internal resistance of $1.00~\Omega.$ (a) What is the current through the external resistor, which has a resistance of $10.00~\Omega$ ? (b) What is the terminal voltage of each battery?

The circuit shows three parallel branches. The first and second branch both have two voltage sources ε with positive terminals upward and internal resistances r. The third branch has a resistor R.

90. Analog meters use a galvanometer, which essentially consists of a coil of wire with a small resistance and a pointer with a scale attached. When current runs through the coil, the pointer turns; the amount the pointer turns is proportional to the amount of current running through the coil. Galvanometers can be used to make an ammeter if a resistor is placed in parallel with the galvanometer. Consider a galvanometer that has a resistance of $25.00~\Omega$ and gives a full scale reading when a $50{\text -}\mu\mathrm{A}$ current runs through it. The galvanometer is to be used to make an ammeter that has a full scale reading of $10.00~\mathrm{A},$ as shown below. Recall that an ammeter is connected in series with the circuit of interest, so all $10~\mathrm{A}$ must run through the meter. (a) What is the current through the parallel resistor in the meter? (b) What is the voltage across the parallel resistor? (c) What is the resistance of the parallel resistor?

The figure shows an ammeter with resistance R subscript M connected across resistor R subscript P with current of 10 A.

91. Analog meters use a galvanometer, which essentially consists of a coil of wire with a small resistance and a pointer with a scale attached. When current runs through the coil, the point turns; the amount the pointer turns is proportional to the amount of current running through the coil. Galvanometers can be used to make a voltmeter if a resistor is placed in series with the galvanometer. Consider a galvanometer that has a resistance of $25.00~\Omega$ and gives a full scale reading when a $50{\text -}\mu\mathrm{A}$ current runs through it. The galvanometer is to be used to make an voltmeter that has a full scale reading of $10.00~\mathrm{V},$ as shown below. Recall that a voltmeter is connected in parallel with the component of interest, so the meter must have a high resistance or it will change the current running through the component. (a) What is the potential drop across the series resistor in the meter? (b) What is the resistance of the parallel resistor?

The figure shows a resistor R subscript S connected in series with a voltmeter with resistance R subscript M. The voltage difference across the ends is 10 V.

92. Consider the circuit shown below. Find $I_1,$ $V_1,$ $I_2,$ and $V_3.$

The circuit shows positive terminal of voltage source V of 12 V connected to an ammeter connected to resistor R subscript 1 of 1 Ω with voltmeter across it connected to two parallel branches. The first branch has an ammeter connected to resistor R subscript 2 of 6 Ω and second branch has R subscript 3 of 13 Ω and voltmeter across it.

93. Consider the circuit below. (a) What is the $RC$ time constant of the circuit? (b) What is the initial current in the circuit once the switch is closed? (c) How much time passes between the instant the switch is closed and the time the current has reached half of the initial current?

94. Consider the circuit below. (a) What is the initial current through resistor $R_2$ when the switch is closed? (b) What is the current through resistor $R_2$ when the capacitor is fully charged, long after the switch is closed? (c) What happens if the switch is opened after it has been closed for some time? (d) If the switch has been closed for a time period long enough for the capacitor to become fully charged, and then the switch is opened, how long before the current through resistor $R_1$ reaches half of its initial value?

The positive terminal of voltage source V subscript 1 of 24 V is connected to an open switch. The other end of the switch is connected to two parallel branches, one with resistor R subscript 1 of 10 kΩ and other with capacitor C of 10 μF. The two branches are connected to source V subscript 1 through resistor R subscript 2 of 30 kΩ.

95. Consider the infinitely long chain of resistors shown below. What is the resistance between terminals $a$ and $b$ ?

The circuit shows infinitely long circuit with vertical resistor R and its two ends connected to horizontal branches with resistors R connected to vertical resistor R connected to horizontal branches with resistors R and so on..

96. Consider the circuit below. The capacitor has a capacitance of $10~\mathrm{mF}.$ The switch is closed and after a long time the capacitor is fully charged. (a) What is the current through each resistor a long time after the switch is closed? (b) What is the voltage across each resistor a long time after the switch is closed? (c) What is the voltage across the capacitor a long time after the switch is closed? (d) What is the charge on the capacitor a long time after the switch is closed? (e) The switch is then opened. The capacitor discharges through the resistors. How long from the time before the current drops to one fifth of the initial value?

97. A $120{\text -}\mathrm{V}$ immersion heater consists of a coil of wire that is placed in a cup to boil the water. The heater can boil one cup of $20.00~^{\circ}\mathrm{C}$ water in $180.00$ seconds. You buy one to use in your dorm room, but you are worried that you will overload the circuit and trip the $15.00{\text -}\mathrm{A},$ $120{\text -}\mathrm{V}$ circuit breaker, which supplies your dorm room. In your dorm room, you have four $100.00{\text -}\mathrm{W}$ incandescent lamps and a $1500.00{\text -}\mathrm{W}$ space heater. (a) What is the power rating of the immersion heater? (b) Will it trip the breaker when everything is turned on? (c) If it you replace the incandescent bulbs with $18.00{\text -}\mathrm{W}$ LED, will the breaker trip when everything is turned on?

98. Find the resistance that must be placed in series with a $25.0{\text -}\Omega$ galvanometer having a $50.0{\text -}\mu\mathrm{A}$ sensitivity (the same as the one discussed in the text) to allow it to be used as a voltmeter with a $3000{\text -}\mathrm{V}$ full-scale reading. Include a circuit diagram with your solution.

99. Find the resistance that must be placed in parallel with a $60.0{\text -}\Omega$ galvanometer having a $1.00{\text -}\mathrm{mA}$ sensitivity (the same as the one discussed in the text) to allow it to be used as an ammeter with a $25.0{\text -}\mathrm{A}$ full-scale reading. Include a circuit diagram with your solution.

License

Icon for the Creative Commons Attribution 4.0 International License