8.4 Magnetic Force on a Current-Carrying Conductor

Samuel J. Ling; Jeff Sanny; William Moebs; Daryl Janzen

8.4 Magnetic Force on a Current-Carrying Conductor

LEARNING OBJECTIVES

By the end of this section, you will be able to:

Determine the direction in which a current-carrying wire experiences a force in an external magnetic field
Calculate the force on a current-carrying wire in an external magnetic field

Moving charges experience a force in a magnetic field. If these moving charges are in a wire—that is, if the wire is carrying a current—the wire should also experience a force. However, before we discuss the force exerted on a current by a magnetic field, we first examine the magnetic field generated by an electric current. We are studying two separate effects here that interact closely: A current-carrying wire generates a magnetic field and the magnetic field exerts a force on the current-carrying wire.

Magnetic Fields Produced by Electrical Currents

When discussing historical discoveries in magnetism, we mentioned Oersted’s finding that a wire carrying an electrical current caused a nearby compass to deflect. A connection was established that electrical currents produce magnetic fields. (This connection between electricity and magnetism is discussed in more detail in Sources of Magnetic Fields.)

The compass needle near the wire experiences a force that aligns the needle tangent to a circle around the wire. Therefore, a current-carrying wire produces circular loops of magnetic field. To determine the direction of the magnetic field generated from a wire, we use a second right-hand rule. In RHR-2, your thumb points in the direction of the current while your fingers wrap around the wire, pointing in the direction of the magnetic field produced (Figure 8.4.1). If the magnetic field were coming at you or out of the page, we represent this with a dot. If the magnetic field were going into the page, we represent this with an $\times$ . These symbols come from considering a vector arrow: An arrow pointed toward you, from your perspective, would look like a dot or the tip of an arrow. An arrow pointed away from you, from your perspective, would look like a cross or an $\times$ . A composite sketch of the magnetic circles is shown in Figure 8.4.1, where the field strength is shown to decrease as you get farther from the wire by loops that are farther separated.

(Figure 8.4.1) $\begin{gather*}.\end{gather*}$

Figure a shows the right hand rule applied to a wire carrying an upward current. The right hand is placed so that the thumb points up, in the direction of the current. The fingers curl around the wire. The magnetic field is out of the page to the left of the current and into the page to the right of the current. Figure b shows the magnetic field lines for the upward current. The field lines form concentric rings that circulate in the same direction as the fingers of the right hand in figure a. The spacing between rings increases with distance from the current. — **Figure 8.4.1** (a) When the wire is in the plane of the paper, the field is perpendicular to the paper. Note the symbols used for the field pointing inward (like the tail of an arrow) and the field pointing outward (like the tip of an arrow). (b) A long and straight wire creates a field with magnetic field lines forming circular loops.

Calculating the Magnetic Force

Electric current is an ordered movement of charge. A current-carrying wire in a magnetic field must therefore experience a force due to the field. To investigate this force, let’s consider the infinitesimal section of wire as shown in Figure 8.4.2. The length and cross-sectional area of the section are dl and A, respectively, so its volume is $V=A\cdot dl$ . The wire is formed from material that contains $n$ charge carriers per unit volume, so the number of charge carriers in the section is $nA\cdot dl$ . If the charge carriers move with drift velocity $\vec{\mathbf{v}}_{\mathrm{d}}$ , the current $I$ in the wire is (from Current and Resistance)

$I=neAv_d.$

The magnetic force on any single charge carrier is $e\vec{\mathbf{v}}_{\mathrm{d}}\times\vec{\mathbf{B}}$ , so the total magnetic force $d\vec{\mathbf{F}}$ on the $nA\cdot dl$ charge carriers in the section of wire is

(8.4.1) $\begin{equation*}d\vec{\mathbf{F}}=(nA\cdot dl)e\vec{\mathbf{v}}_{\mathrm{d}}\times\vec{\mathbf{B}}.\end{equation*}$

We can define $dl$ to be a vector of length $dl$ pointing along $\vec{\mathbf{v}}_{\mathrm{d}}$ , which allows us to rewrite this equation as

(8.4.2) $\begin{equation*}d\vec{\mathbf{F}}=neAv_{\mathrm{d}}\vec{\mathbf{dl}}\times\vec{\mathbf{B}},\end{equation*}$

or

(8.4.3) $\begin{equation*}d\vec{\mathbf{F}}=I\vec{\mathbf{dl}}\times\vec{\mathbf{B}}.\end{equation*}$

This is the magnetic force on the section of wire. Note that it is actually the net force exerted by the field on the charge carriers themselves. The direction of this force is given by RHR-1, where you point your fingers in the direction of the current and curl them toward the field. Your thumb then points in the direction of the force.

(Figure 8.4.2) $\begin{gather*}.\end{gather*}$

An illustration of a curving current-carrying wire in a uniform magnetic field. A detail view of a small segment of the wire shows a short, straight piece of current, length d l with current I though it. The velocity v sub d is in the direction of the current. The field B makes an angle theta with the velocity vector. — **Figure 8.4.2** An infinitesimal section of current-carrying wire in a magnetic field.

To determine the magnetic force $\vec{\mathbf{F}}$ on a wire of arbitrary length and shape, we must integrate 8.4.3 over the entire wire. If the wire section happens to be straight and B is uniform, the equation differentials become absolute quantities, giving us

(8.4.4) $\begin{equation*}\vec{\mathbf{F}}=I\vec{\mathbf{l}}\times\vec{\mathbf{B}}.\end{equation*}$

This is the force on a straight, current-carrying wire in a uniform magnetic field.

EXAMPLE 8.4.1

Balancing the Gravitational and Magnetic Forces on a Current-Carrying Wire

A wire of length $50~\mathrm{cm}$ and mass $10~\mathrm{g}$ is suspended in a horizontal plane by a pair of flexible leads (Figure 8.4.3). The wire is then subjected to a constant magnetic field of magnitude $0.50~\mathrm{T}$ , which is directed as shown. What are the magnitude and direction of the current in the wire needed to remove the tension in the supporting leads?

(Figure 8.4.3) $\begin{gather*}.\end{gather*}$

Figure a: An illustration of a wire suspended in a uniform magnetic field. The magnetic field points into the page. The wire is horizontal and is 50 cm long. A variable voltage source completes the circuit made by the wire and the leads used to suspend it. Figure b: A free body diagram of the wire. The current is to the right. The weight, mg, points down. Tension at either end is up. The magnetic force is up. — **Figure 8.4.3** (a) A wire suspended in a magnetic field. (b) The free-body diagram for the wire.

Strategy

From the free-body diagram in the figure, the tensions in the supporting leads go to zero when the gravitational and magnetic forces balance each other. Using the RHR-1, we find that the magnetic force points up. We can then determine the current $I$ by equating the two forces.

Solution

Equate the two forces of weight and magnetic force on the wire:

$mg=IlB.$

Thus,

$I=\frac{mg}{lB}=\frac{(0.010~\mathrm{kg})(9.8~\mathrm{m/s}^2)}{(0.50~\mathrm{m})(0.50~\mathrm{T})}=0.39~\mathrm{A}.$

Significance

This large magnetic field creates a significant force on a length of wire to counteract the weight of the wire.

EXAMPLE 8.4.2

Calculating Magnetic Force on a Current-Carrying Wire

A long, rigid wire lying along the $y{\text -}$ axis carries a $5.0{\text -}A$ current flowing in the positive $y{\text -}$ direction. (a) If a constant magnetic field of magnitude $0.30~\mathrm{T}$ is directed along the positive $x{\text -}$ axis, what is the magnetic force per unit length on the wire? (b) If a constant magnetic field of $0.30~\mathrm{T}$ is directed $30$ degrees from the $+x{\text -}$ axis towards the $+y{\text -}$ axis, what is the magnetic force per unit length on the wire?

Strategy

The magnetic force on a current-carrying wire in a magnetic field is given by $\vec{\mathbf{F}}=I\vec{\mathbf{l}}\times\vec{\mathbf{B}}$ . For part a, since the current and magnetic field are perpendicular in this problem, we can simplify the formula to give us the magnitude and find the direction through the RHR-1. The angle $\theta$ is $90$ degrees, which means $\sin\theta=1$ . Also, the length can be divided over to the left-hand side to find the force per unit length. For part b, the current times length is written in unit vector notation, as well as the magnetic field. After the cross product is taken, the directionality is evident by the resulting unit vector.

Solution

a. We start with the general formula for the magnetic force on a wire. We are looking for the force per unit length, so we divide by the length to bring it to the left-hand side. We also set $\sin\theta=1$ . The solution therefore is

$\begin{eqnarray*}F&=&ILB\sin\theta\\\frac{F}{l}&=&(5.0~\mathrm{A})(0.30~\mathrm{T})\\\frac{F}{l}&=&1.5~\mathrm{N/m}.\end{eqnarray*}$

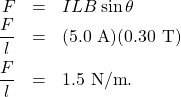
Directionality: Point your fingers in the positive $y{\text -}$ direction and curl your fingers in the positive $x{\text -}$ direction. Your thumb will point in the $-\hat{\mathbf{k}}$ direction. Therefore, with directionality, the solution is

$frac{\vec{\mathbf{F}}}{l}&=&1.5\hat{\mathbf{k}}~\mathrm{N/m}.$

b. The current times length and the magnetic field are written in unit vector notation. Then, we take the cross product to find the force:

\begin{eqnarray*}\vec{\mathbf{F}}&=&I\vec{\mathbf{L}}\times\vec{\mathbf{B}}=(5.0~\mathrm{A})l\hat{\mathbf{j}}\times\left((0.30~\mathrm{T})\cos(30^{\circ})\hat{\mathbf{i}}+(0.30~\mathrm{T})\sin(30^{\circ})\hat{\mathbf{j}}\right)\\\vec{\mathbf{F}}/l&=&-1.30\hat{\mathbf{k}}~\mathrm{N/m}.\end{eqnarray*}

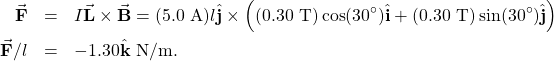
Significance

This large magnetic field creates a significant force on a small length of wire. As the angle of the magnetic field becomes more closely aligned to the current in the wire, there is less of a force on it, as seen from comparing parts a and b.

CHECK YOUR UNDERSTANDING 8.3

A straight, flexible length of copper wire is immersed in a magnetic field that is directed into the page. (a) If the wire’s current runs in the $+x{\text -}$ direction, which way will the wire bend? (b) Which way will the wire bend if the current runs in the $-x{\text -}$ direction?

EXAMPLE 8.4.3

Force on a Circular Wire

A circular current loop of radius $R$ carrying a current $I$ is placed in the $xy{\text -}$ plane. A constant uniform magnetic field cuts through the loop parallel to the $y{\text -}$ axis (Figure 8.4.4). Find the magnetic force on the upper half of the loop, the lower half of the loop, and the total force on the loop.

(Figure 8.4.4) $\begin{gather*}.\end{gather*}$

A loop of radius R is in the plane of the page. The loop carries a clockwise current I and is in a uniform magnetic field that points up the page. — **Figure 8.4.4** A loop of wire carrying a current in a magnetic field.

Strategy

The magnetic force on the upper loop should be written in terms of the differential force acting on each segment of the loop. If we integrate over each differential piece, we solve for the overall force on that section of the loop. The force on the lower loop is found in a similar manner, and the total force is the addition of these two forces.

Solution

A differential force on an arbitrary piece of wire located on the upper ring is:

$dF=IB\sin\theta dl.$

where $\theta$ is the angle between the magnetic field direction ( $+y$ ) and the segment of wire. A differential segment is located at the same radius, so using an arc-length formula, we have:

$\begin{eqnarray*}dl&=&Rd\theta\\dF&=&IBR\sin\theta d\theta.\end{eqnarray*}$

In order to find the force on a segment, we integrate over the upper half of the circle, from 0 to $\pi$ . This results in:

$F=IBR\int_0^{\pi}\sin\theta d\theta=IBR(-\cos\pi+\cos0)=2IBR.$

The lower half of the loop is integrated from $\pi$ to zero, giving us:

$F=IBR\int_{\pi}^{0}\sin\theta d\theta=IBR(-\cos0+\cos\pi)=-2IBR.$

The net force is the sum of these forces, which is zero.

Significance

The total force on any closed loop in a uniform magnetic field is zero. Even though each piece of the loop has a force acting on it, the net force on the system is zero. (Note that there is a net torque on the loop, which we consider in the next section.)

License

Icon for the Creative Commons Attribution 4.0 International License