5.2 Model of Conduction in Metals

Samuel J. Ling; Jeff Sanny; William Moebs; Daryl Janzen

5.2 Model of Conduction in Metals

LEARNING OBJECTIVES

By the end of this section, you will be able to:

Define the drift velocity of charges moving through a metal
Define the vector current density
Describe the operation of an incandescent lamp

When electrons move through a conducting wire, they do not move at a constant velocity, that is, the electrons do not move in a straight line at a constant speed. Rather, they interact with and collide with atoms and other free electrons in the conductor. Thus, the electrons move in a zig-zag fashion and drift through the wire. We should also note that even though it is convenient to discuss the direction of current, current is a scalar quantity. When discussing the velocity of charges in a current, it is more appropriate to discuss the current density. We will come back to this idea at the end of this section.

Drift Velocity

Electrical signals move very rapidly. Telephone conversations carried by currents in wires cover large distances without noticeable delays. Lights come on as soon as a light switch is moved to the ‘on’ position. Most electrical signals carried by currents travel at speeds on the order of $10^8~\mathrm{m/s}$ , a significant fraction of the speed of light. Interestingly, the individual charges that make up the current move much slower on average, typically drifting at speeds on the order of $10^{-4}~\mathrm{m/s}$ . How do we reconcile these two speeds, and what does it tell us about standard conductors?

The high speed of electrical signals results from the fact that the force between charges acts rapidly at a distance. Thus, when a free charge is forced into a wire, as in Figure 5.2.1, the incoming charge pushes other charges ahead of it due to the repulsive force between like charges. These moving charges push on charges farther down the line. The density of charge in a system cannot easily be increased, so the signal is passed on rapidly. The resulting electrical shock wave moves through the system at nearly the speed of light. To be precise, this fast-moving signal, or shock wave, is a rapidly propagating change in the electrical field.

(Figure 5.2.1) $\begin{gather*}.\end{gather*}$

Picture is a schematic drawing of electrons flowing from left to right through the wire. — **Figure 5.2.1** When charged particles are forced into this volume of a conductor, an equal number are quickly forced to leave. The repulsion between like charges makes it difficult to increase the number of charges in a volume. Thus, as one charge enters, another leaves almost immediately, carrying the signal rapidly forward.

Good conductors have large numbers of free charges. In metals, the free charges are free electrons. (In fact, good electrical conductors are often good heat conductors too, because large numbers of free electrons can transport thermal energy as well as carry electrical current.) Figure 5.2.2 shows how free electrons move through an ordinary conductor. The distance that an individual electron can move between collisions with atoms or other electrons is quite small. The electron paths thus appear nearly random, like the motion of atoms in a gas. But there is an electrical field in the conductor that causes the electrons to drift in the direction shown (opposite to the field, since they are negative). The drift velocity $\vec{\mathbf{v}}_{\mathrm{d}}$ is the average velocity of the free charges. Drift velocity is quite small, since there are so many free charges. If we have an estimate of the density of free electrons in a conductor, we can calculate the drift velocity for a given current. The larger the density, the lower the velocity required for a given current.

(Figure 5.2.2) $\begin{gather*}.\end{gather*}$

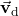Picture is a schematic drawing of a collision path of an electron that moves with the velocity vd from left to right through the wire. — **Figure 5.2.2** Free electrons moving in a conductor make many collisions with other electrons and other particles. A typical path of one electron is shown. The average velocity of the free charges is called the drift velocity $\vec{\mathbf{v}}_{\mathrm{d}}$ and for electrons, it is in the direction opposite to the electrical field. The collisions normally transfer energy to the conductor, requiring a constant supply of energy to maintain a steady current.

Free-electron collisions transfer energy to the atoms of the conductor. The electrical field does work in moving the electrons through a distance, but that work does not increase the kinetic energy (nor speed) of the electrons. The work is transferred to the conductor’s atoms, often increasing temperature. Thus, a continuous power input is required to keep a current flowing. (An exception is superconductors, for reasons we shall explore in a later chapter. Superconductors can have a steady current without a continual supply of energy—a great energy savings.) For a conductor that is not a superconductor, the supply of energy can be useful, as in an incandescent light bulb filament (Figure 5.2.3). The supply of energy is necessary to increase the temperature of the tungsten filament, so that the filament glows.

(Figure 5.2.3) $\begin{gather*}.\end{gather*}$

Left picture is a schematic drawing of an incandescent bulb. It shows point of contact separated by the insulator from the rest of the bulb. Wire goes from the point of contact to the tungsten filament. Wire and tungsten filament are encapsulated by the glass envelope. Right picture is a photograph of the incandescent bulb with glowing filament. — **Figure 5.2.3** The incandescent lamp is a simple design. A tungsten filament is placed in a partially evacuated glass envelope. One end of the filament is attached to the screw base, which is made out of a conducting material. The second end of the filament is attached to a second contact in the base of the bulb. The two contacts are separated by an insulating material. Current flows through the filament, and the temperature of the filament becomes large enough to cause the filament to glow and produce light. However, these bulbs are not very energy efficient, as evident from the heat coming from the bulb. In the year 2012, the United States, along with many other countries, began to phase out incandescent lamps in favor of more energy-efficient lamps, such as light-emitting diode (LED) lamps and compact fluorescent lamps (CFL) (credit right: modification of work by Serge Saint).

We can obtain an expression for the relationship between current and drift velocity by considering the number of free charges in a segment of wire, as illustrated in Figure 5.2.4 The number of free charges per unit volume, or the number density of free charges, is given the symbol $n$ where $n=\frac{\mathrm{number~of~charges}}{\mathrm{volume}}$ . The value of $n$ depends on the material. The shaded segment has a volume $Av_{\mathrm{d}}dt$ , so that the number of free charges in the volume is $nAv_{\mathrm{d}}dt$ . The charge $dQ$ in this segment is thus $qnAv_{\mathrm{d}}dt$ where $q$ is the amount of charge on each carrier. (The magnitude of the charge of electrons is $q=1.60\times10^{-19}~\mathrm{C}$ .) Current is charge moved per unit time; thus, if all the original charges move out of this segment in time $dt$ , the current is

$I=\frac{dQ}{dt}=qnAv_{\mathrm{d}}.$

Rearranging terms gives

(5.2.1) $\begin{equation*}v_{\mathrm{d}}=\frac{I}{nqA}\end{equation*}$

where $v_{\mathrm{d}}$ is the drift velocity, $n$ is the free charge density, $A$ is the cross-sectional area of the wire, and $I$ is the current through the wire. The carriers of the current each have charge $q$ and move with a drift velocity of magnitude $v_{\mathrm{d}}$ .

(Figure 5.2.4) $\begin{gather*}.\end{gather*}$

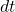Picture is a schematic drawing of charges q flowing from left to right with the speed Vd through the wire with the cross-sectional area A. — **Figure 5.2.4** All the charges in the shaded volume of this wire move out in a time $dt$ , having a drift velocity of magnitude $v_{\mathrm{d}}$ .

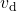Note that simple drift velocity is not the entire story. The speed of an electron is sometimes much greater than its drift velocity. In addition, not all of the electrons in a conductor can move freely, and those that do move might move somewhat faster or slower than the drift velocity. So what do we mean by free electrons?

Atoms in a metallic conductor are packed in the form of a lattice structure. Some electrons are far enough away from the atomic nuclei that they do not experience the attraction of the nuclei as strongly as the inner electrons do. These are the free electrons. They are not bound to a single atom but can instead move freely among the atoms in a “sea” of electrons. When an electrical field is applied, these free electrons respond by accelerating. As they move, they collide with the atoms in the lattice and with other electrons, generating thermal energy, and the conductor gets warmer. In an insulator, the organization of the atoms and the structure do not allow for such free electrons.

As you know, electric power is usually supplied to equipment and appliances through round wires made of a conducting material (copper, aluminum, silver, or gold) that are stranded or solid. The diameter of the wire determines the current-carrying capacity—the larger the diameter, the greater the current-carrying capacity. Even though the current-carrying capacity is determined by the diameter, wire is not normally characterized by the diameter directly. Instead, wire is commonly sold in a unit known as “gauge.” Wires are manufactured by passing the material through circular forms called “drawing dies.” In order to make thinner wires, manufacturers draw the wires through multiple dies of successively thinner diameter. Historically, the gauge of the wire was related to the number of drawing processes required to manufacture the wire. For this reason, the larger the gauge, the smaller the diameter. In the United States, the American Wire Gauge (AWG) was developed to standardize the system. Household wiring commonly consists of $10{\text -}\mathrm{gauge}$ ( $2.588{\text -}\mathrm{mm}$ diameter) to $14{\text -}\mathrm{gauge}$ ( $1.626{\text -}\mathrm{mm}$ diameter) wire. A device used to measure the gauge of wire is shown in Figure 5.2.5.

(Figure 5.2.5) $\begin{gather*}.\end{gather*}$

Picture is a photograph of a device used for measuring the gauge of electrical wire. The higher gauge numbers indicate thinner wires. — Figure 5.2.5 A device for measuring the gauge of electrical wire. As you can see, higher gauge numbers indicate thinner wires.

EXAMPLE 5.2.1

Calculating Drift Velocity in a Common Wire

Calculate the drift velocity of electrons in a copper wire with a diameter of $2.053~\mathrm{mm}$ ( $12{\text -}\mathrm{gauge}$ ) carrying a $20.0{\text -}\mathrm{A}$ current, given that there is one free electron per copper atom. (Household wiring often contains $12{\text -}\mathrm{gauge}$ copper wire, and the maximum current allowed in such wire is usually $20.0~\mathrm{A}$ .) The density of copper is $8.80\times10^{3}~\mathrm{kg/m}^3$ and the atomic mass of copper is $63.54~\mathrm{g/mol}$ .

Strategy

We can calculate the drift velocity using the equation $I=nqAv_{\mathrm{d}}$ . The current is $I=20.0~\mathrm{A}$ and $q=-1.60\times10^{-19}~\mathrm{C}$ is the charge of an electron. We can calculate the area of a cross-section of the wire using the formula $A=\pi r^2$ where $r$ is one-half the diameter. The given diameter is $2.053~\mathrm{mm}$ , so $r$ is $1.0265~\mathrm{mm}$ . We are given the density of copper, $8.80\times10^{3}~\times10^3~\mathrm{kg/m}^3$ , and the atomic mass of copper is $63.54~\mathrm{g/mol}$ . We can use these two quantities along with Avogadro’s number, $6.02\times10^{23}~\mathrm{atoms/mol}$ , to determine $n$ , the number of free electrons per cubic meter.

Solution

First, we calculate the density of free electrons in copper. There is one free electron per copper atom. Therefore, the number of free electrons is the same as the number of copper atoms per $\mathrm{m}^3$ . We can now find $n$ as follows:

$\begin{eqnarray*}n&=&\frac{1 e^{-}}{\mathrm{atom}}\times\frac{6.02\times10^{23}~\mathrm{atoms}}{\mathrm{mol}}\times\frac{1~\mathrm{mol}}{63.54~\mathrm{g}}\times\frac{1000~\mathrm{g}}{\mathrm{kg}}\times\frac{8.80\times10^3~\mathrm{kg}}{1~\mathrm{m}^3}\\&=&8.34\times10^{28}e^{-}/\mathrm{m}^3.\end{eqnarray*}$

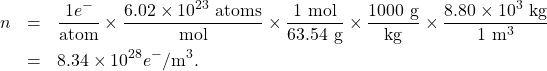
The cross-sectional area of the wire is

$A=\pi r^2=\pi\left(\frac{2.05\times10^{-3}~\mathrm{m}}{2}\right)^2=3.30\times10^{-6}~\mathrm{m}^2.$

Rearranging $I=nqAv_{\mathrm{d}}$ to isolate drift velocity gives

$\begin{eqnarray*}v_{\mathrm{d}}&=&\frac{I}{nqA}=\frac{20.0~\mathrm{A}}{(8.34\times10^{28}e^-/\mathrm{m}^3)(-1.60\times10^{-19}~\mathrm{C}/e^-)(3.30\times10^{-6}~\mathrm{m}^2)}\\&=&-4.54\times10^{-4}~\mathrm{m/s}.\end{eqnarray*}$

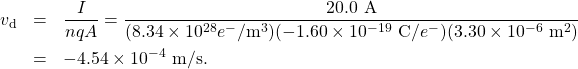
Significance

The minus sign indicates that the negative charges are moving in the direction opposite to conventional current. The small value for drift velocity (on the order of $10^{-4}~\mathrm{m/s}$ ) confirms that the signal moves on the order of $10^2$ times faster (about $10^8~\mathrm{m/s}$ ) than the charges that carry it.

CHECK YOUR UNDERSTANDING 5.3

In Example 5.2.2, the drift velocity was calculated for a $2.053{\text -}\mathrm{mm}$ diameter ( $12{\text -}\mathrm{gauge}$ ) copper wire carrying a $20{\text -}\mathrm{A}$ current. Would the drift velocity change for a $1.628{\text -}\mathrm{mm}$ diameter ( $14{\text -}\mathrm{gauge}$ ) wire carrying the same $20{\text -}\mathrm{A}$ current?

Current Density

Although it is often convenient to attach a negative or positive sign to indicate the overall direction of motion of the charges, current is a scalar quantity, $I=\frac{dQ}{dt}$ . It is often necessary to discuss the details of the motion of the charge, instead of discussing the overall motion of the charges. In such cases, it is necessary to discuss the current density, $\vec{\mathbf{J}}$ , a vector quantity. The current density is the flow of charge through an infinitesimal area, divided by the area. The current density must take into account the local magnitude and direction of the charge flow, which varies from point to point. The unit of current density is ampere per meter squared, and the direction is defined as the direction of net flow of positive charges through the area.

The relationship between the current and the current density can be seen in Figure 5.2.6. The differential current flow through the area $d\vec{\mathbf{A}}$ is found as

$dI=\vec{\mathbf{J}}\cdot d\vec{\mathbf{A}}=JdA\cos\theta,$

where $\theta$ is the angle between the area and the current density. The total current passing through area $d\vec{\mathbf{A}}$ can be found by integrating over the area,

(5.2.2) $\begin{equation*}I=\iint_{\mathrm{area}}\vec{\mathbf{J}}\cdot d\vec{\mathbf{A}}.\end{equation*}$

Consider the magnitude of the current density, which is the current divided by the area:

$J=\frac{I}{A}=\frac{n|q|Av_{\mathrm{d}}}{A}=n|q|v_{\mathrm{d}}.$

Thus, the current density is $\vec{\mathbf{J}}=nq\vec{\mathbf{v}}_{\mathrm{d}}$ . If $q$ is positive, $\vec{\mathbf{v}}_{\mathrm{d}}$ is in the same direction as the electrical field $\vec{\mathbf{E}}$ . If $q$ is negative, $\vec{\mathbf{v}}_{\mathrm{d}}$ is in the opposite direction of $\vec{\mathbf{E}}$ . Either way, the direction of the current density $\vec{\mathbf{J}}$ is in the direction of the electrical field $\vec{\mathbf{E}}$ .

(Figure 5.2.6) $\begin{gather*}.\end{gather*}$

Picture is a schematic drawing of current flowing through the wire. Current density J forms an angle theta with the dA. — **Figure 5.2.6** The current density $\vec{\mathbf{J}}$ is defined as the current passing through an infinitesimal cross-sectional area divided by the area. The direction of the current density is the direction of the net flow of positive charges and the magnitude is equal to the current divided by the infinitesimal area.

EXAMPLE 5.2.2

Calculating the Current Density in a Wire

The current supplied to a lamp with a $100{\text -}\mathrm{W}$ light bulb is $0.87~\mathrm{A}$ . The lamp is wired using a copper wire with diameter $2.588~\mathrm{mm}$ ( $10{\text -}\mathrm{gauge}$ ). Find the magnitude of the current density.

Strategy

The current density is the current moving through an infinitesimal cross-sectional area divided by the area. We can calculate the magnitude of the current density using $J=\frac{I}{A}$ . The current is given as $0.87~\mathrm{A}$ . The cross-sectional area can be calculated to be $A=5.26~\mathrm{mm}^2$ .

Solution

Calculate the current density using the given current $I=0.87~\mathrm{A}$ and the area, found to be $A=5.26~\mathrm{mm}^2$ .

$J=\frac{I}{A}=\frac{0.87~\mathrm{A}}{5.26\times10^{-6}~\mathrm{m}^2}=1.65\times10^5~\frac{\mathrm{A}}{\mathrm{m}^2}.$

Significance

The current density in a conducting wire depends on the current through the conducting wire and the cross-sectional area of the wire. For a given current, as the diameter of the wire increases, the charge density decreases.

CHECK YOUR UNDERSTANDING 5.4

The current density is proportional to the current and inversely proportional to the area. If the current density in a conducting wire increases, what would happen to the drift velocity of the charges in the wire?

What is the significance of the current density? The current density is proportional to the current, and the current is the number of charges that pass through a cross-sectional area per second. The charges move through the conductor, accelerated by the electric force provided by the electrical field. The electrical field is created when a voltage is applied across the conductor. In Ohm’s Law, we will use this relationship between the current density and the electrical field to examine the relationship between the current through a conductor and the voltage applied.

License

Icon for the Creative Commons Attribution 4.0 International License