8.3 Motion of a Charged Particle in a Magnetic Field

Samuel J. Ling; Jeff Sanny; William Moebs; Daryl Janzen

8.3 Motion of a Charged Particle in a Magnetic Field

LEARNING OBJECTIVES

By the end of this section, you will be able to:

Explain how a charged particle in an external magnetic field undergoes circular motion
Describe how to determine the radius of the circular motion of a charged particle in a magnetic field

A charged particle experiences a force when moving through a magnetic field. What happens if this field is uniform over the motion of the charged particle? What path does the particle follow? In this section, we discuss the circular motion of the charged particle as well as other motion that results from a charged particle entering a magnetic field.

The simplest case occurs when a charged particle moves perpendicular to a uniform $B$ -field (Figure 8.3.1). If the field is in a vacuum, the magnetic field is the dominant factor determining the motion. Since the magnetic force is perpendicular to the direction of travel, a charged particle follows a curved path in a magnetic field. The particle continues to follow this curved path until it forms a complete circle. Another way to look at this is that the magnetic force is always perpendicular to velocity, so that it does no work on the charged particle. The particle’s kinetic energy and speed thus remain constant. The direction of motion is affected but not the speed.

(Figure 8.3.1) $\begin{gather*}.\end{gather*}$

An illustration of the motion of a charged particle in a uniform magnetic field. The magnetic field points into the page. The particle is negative and moves in a clockwise circle. Its velocity is tangent to the circle, and the force points toward the center of the circle at all times. 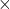— **Figure 8.3.1** A negatively charged particle moves in the plane of the paper in a region where the magnetic field is perpendicular to the paper (represented by the small $\times$ s—like the tails of arrows). The magnetic force is perpendicular to the velocity, so velocity changes in direction but not magnitude. The result is uniform circular motion. (Note that because the charge is negative, the force is opposite in direction to the prediction of the right-hand rule.)

In this situation, the magnetic force supplies the centripetal force $F_c=\frac{mv^2}{r}$ . Noting that the velocity is perpendicular to the magnetic field, the magnitude of the magnetic force is reduced to $F=qvB$ . Because the magnetic force $F$ supplies the centripetal force $F_c$ , we have

(8.3.1) $\begin{equation*}qvB=\frac{mv^2}{r}.\end{equation*}$

Solving for $r$ yields

(8.3.2) $\begin{equation*}r=\frac{mv}{qB}.\end{equation*}$

Here, $r$ is the radius of curvature of the path of a charged particle with mass $m$ and charge $q$ , moving at a speed $v$ that is perpendicular to a magnetic field of strength $B$ . The time for the charged particle to go around the circular path is defined as the period, which is the same as the distance traveled (the circumference) divided by the speed. Based on this and 8.3.1, we can derive the period of motion as

(8.3.3) $\begin{equation*}T=\frac{2\pi r}{v}=\frac{2\pi}{v}\frac{mv}{qB}=\frac{2\pi m}{qB}.\end{equation*}$

If the velocity is not perpendicular to the magnetic field, then we can compare each component of the velocity separately with the magnetic field. The component of the velocity perpendicular to the magnetic field produces a magnetic force perpendicular to both this velocity and the field:

(8.3.4) $\begin{equation*}v_{\mathrm{perp}}=v\sin\theta,~~~v_{\mathrm{para}}=v\cos\theta.\end{equation*}$

where $\theta$ is the angle between $v$ and $B$ . The component parallel to the magnetic field creates constant motion along the same direction as the magnetic field, also shown in 8.3.4. The parallel motion determines the pitch $p$ of the helix, which is the distance between adjacent turns. This distance equals the parallel component of the velocity times the period:

(8.3.5) $\begin{equation*}p=v_{\mathrm{para}}T.\end{equation*}$

The result is a helical motion, as shown in the following figure.

(Figure 8.3.2) $\begin{gather*}.\end{gather*}$

An illustration of a positively charged particle moving in a uniform magnetic field. The field is in the positive x direction. The initial velocity is shown as having a component, v sub para, in the positive x direction and another component, v sub perp, in the positive y direction. The particle moves in a helix that loops in the y z plane (counterclockwise from the particle’s perspective) and advances in the positive x direction. — **Figure 8.3.2** A charged particle moving with a velocity not in the same direction as the magnetic field. The velocity component perpendicular to the magnetic field creates circular motion, whereas the component of the velocity parallel to the field moves the particle along a straight line. The pitch is the horizontal distance between two consecutive circles. The resulting motion is helical.

While the charged particle travels in a helical path, it may enter a region where the magnetic field is not uniform. In particular, suppose a particle travels from a region of strong magnetic field to a region of weaker field, then back to a region of stronger field. The particle may reflect back before entering the stronger magnetic field region. This is similar to a wave on a string traveling from a very light, thin string to a hard wall and reflecting backward. If the reflection happens at both ends, the particle is trapped in a so-called magnetic bottle.

Trapped particles in magnetic fields are found in the Van Allen radiation belts around Earth, which are part of Earth’s magnetic field. These belts were discovered by James Van Allen while trying to measure the flux of cosmic rays on Earth (high-energy particles that come from outside the solar system) to see whether this was similar to the flux measured on Earth. Van Allen found that due to the contribution of particles trapped in Earth’s magnetic field, the flux was much higher on Earth than in outer space. Aurorae, like the famous aurora borealis (northern lights) in the Northern Hemisphere (Figure 8.3.3), are beautiful displays of light emitted as ions recombine with electrons entering the atmosphere as they spiral along magnetic field lines. (The ions are primarily oxygen and nitrogen atoms that are initially ionized by collisions with energetic particles in Earth’s atmosphere.) Aurorae have also been observed on other planets, such as Jupiter and Saturn.

(Figure 8.3.3) $\begin{gather*}.\end{gather*}$

Figure a is an illustration of the Van Allen radiation belts. Charged particles move in helices parallel to the field lines and trapped between them. Figure b is a photograph of the aurora borealis. — **Figure 8.3.3** (a) The Van Allen radiation belts around Earth trap ions produced by cosmic rays striking Earth’s atmosphere. (b) The magnificent spectacle of the aurora borealis, or northern lights, glows in the northern sky above Bear Lake near Eielson Air Force Base, Alaska. Shaped by Earth’s magnetic field, this light is produced by glowing molecules and ions of oxygen and nitrogen. (credit b: modification of work by USAF Senior Airman Joshua Strang)

EXAMPLE 8.3.1

Beam Deflector

A research group is investigating short-lived radioactive isotopes. They need to design a way to transport alpha-particles (helium nuclei) from where they are made to a place where they will collide with another material to form an isotope. The beam of alpha-particles $\left(m=6.64\times10^{-27}~\mathrm{kg},\ q=3.2\times10^{-19}~\mathrm{C}\right)$ bends through a $90{\text -}$ degree region with a uniform magnetic field of $0.050~\mathrm{T}$ (Figure 8.3.4). (a) In what direction should the magnetic field be applied? (b) How much time does it take the alpha-particles to traverse the uniform magnetic field region?

(Figure 8.3.4) $\begin{gather*}.\end{gather*}$

An illustration of the proposed device. Alpha particles enter the bottom of an evacuated pipe, moving upward. The pipe makes a 90 degree bend, radius r, to the left, then continues horizontally. The particle beam exits to the left. The bend is in a region with uniform magnetic field. — **Figure 8.3.4** Top view of the beam deflector setup.

Strategy

a. The direction of the magnetic field is shown by the RHR-1. Your fingers point in the direction of $v$ , and your thumb needs to point in the direction of the force, to the left. Therefore, since the alpha-particles are positively charged, the magnetic field must point down.

b. The period of the alpha-particle going around the circle is

(8.3.6) $\begin{equation*}T=\frac{2\pi m}{qB}.\end{equation*}$

Because the particle is only going around a quarter of a circle, we can take $0.25$ times the period to find the time it takes to go around this path.

Solution

a. Let’s start by focusing on the alpha-particle entering the field near the bottom of the picture. First, point your thumb up the page. In order for your palm to open to the left where the centripetal force (and hence the magnetic force) points, your fingers need to change orientation until they point into the page. This is the direction of the applied magnetic field.

b. The period of the charged particle going around a circle is calculated by using the given mass, charge, and magnetic field in the problem. This works out to be

$T=\frac{2\pi m}{qB}=\frac{2\pi\left(6.64\times10^{-27}~\mathrm{kg}\right)}{\left(3.2\times10^{-19}~\mathrm{C}\right)(0.050~\mathrm{T})}=2.6\times10^{-6}~\mathrm{s}.$

However, for the given problem, the alpha-particle goes around a quarter of the circle, so the time it takes would be

$t=0.25\times2.61\times10^{-6}~\mathrm{s}=6.5\times10^{-7}~\mathrm{s}.$

Significance

This time may be quick enough to get to the material we would like to bombard, depending on how short-lived the radioactive isotope is and continues to emit alpha-particles. If we could increase the magnetic field applied in the region, this would shorten the time even more. The path the particles need to take could be shortened, but this may not be economical given the experimental setup.

CHECK YOUR UNDERSTANDING 8.2

A uniform magnetic field of magnitude $1.5~\mathrm{T}$ is directed horizontally from west to east. (a) What is the magnetic force on a proton at the instant when it is moving vertically downward in the field with a speed of $4.7\times10^7~\mathrm{m/s}$ ? (b) Compare this force with the weight $w$ of a proton.

EXAMPLE 8.3.2

Helical Motion in a Magnetic Field

A proton enters a uniform magnetic field of $1.0\times10^{-4}~\mathrm{T}$ with a speed of $5\times10^5~\mathrm{m/s}$ . At what angle must the magnetic field be from the velocity so that the pitch of the resulting helical motion is equal to the radius of the helix?

Strategy

The pitch of the motion relates to the parallel velocity times the period of the circular motion, whereas the radius relates to the perpendicular velocity component. After setting the radius and the pitch equal to each other, solve for the angle between the magnetic field and velocity or $\theta$ .

Solution

The pitch is given by Equation 8.3.5, the period is given by Equation 8.3.3, and the radius of circular motion is given by Equation 8.3.2. Note that the velocity in the radius equation is related to only the perpendicular velocity, which is where the circular motion occurs. Therefore, we substitute the sine component of the overall velocity into the radius equation to equate the pitch and radius:

$\begin{eqnarray*}p&=&r\\v_{\parallel}T&=&\frac{mv_{\perp}}{qB}\\v\cos\theta\frac{2\pi m}{qB}&=&\frac{mv\sin\theta}{qB}\\2\pi&=&\tan\theta\\\theta&=&81.0^{\circ}.\end{eqnarray*}$

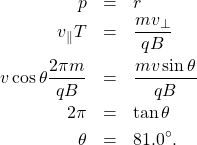
Significance

If this angle were $0^{\circ}$ , only parallel velocity would occur and the helix would not form, because there would be no circular motion in the perpendicular plane. If this angle were $90^{\circ}$ , only circular motion would occur and there would be no movement of the circles perpendicular to the motion. That is what creates the helical motion.

License

Icon for the Creative Commons Attribution 4.0 International License