12.6 Transformers
LEARNING OBJECTIVES
- Explain why power plants transmit electricity at high voltages and low currents and how they do this
- Develop relationships among current, voltage, and the number of windings in step-up and step-down transformers
Although ac electric power is produced at relatively low voltages, it is sent through transmission lines at very high voltages (as high as ![]() ). The same power can be transmitted at different voltages because power is the product
). The same power can be transmitted at different voltages because power is the product ![]() (For simplicity, we ignore the phase factor
(For simplicity, we ignore the phase factor ![]() ) A particular power requirement can therefore be met with a low voltage and a high current or with a high voltage and a low current. The advantage of the high-voltage/low-current choice is that it results in lower
) A particular power requirement can therefore be met with a low voltage and a high current or with a high voltage and a low current. The advantage of the high-voltage/low-current choice is that it results in lower ![]() ohmic losses in the transmission lines, which can be significant in lines that are many kilometres long (Figure 12.6.1).
ohmic losses in the transmission lines, which can be significant in lines that are many kilometres long (Figure 12.6.1).
(Figure 12.6.1) ![]()
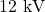 to
to 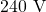 so that it can be safely introduced into a home. A high-voltage transmission line allows a low current to be transmitted via a substation over long distances.
so that it can be safely introduced into a home. A high-voltage transmission line allows a low current to be transmitted via a substation over long distances.Typically, the alternating emfs produced at power plants are “stepped up” to very high voltages before being transmitted through power lines; then, they must be “stepped down” to relatively safe values (![]() or
or ![]() rms) before they are introduced into homes. The device that transforms voltages from one value to another using induction is the transformer (Figure 12.6.2).
rms) before they are introduced into homes. The device that transforms voltages from one value to another using induction is the transformer (Figure 12.6.2).
(Figure 12.6.2) ![]()
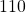 to
to 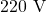 used in homes. (credit: modification of work by “Fortyseven”/Flickr)
used in homes. (credit: modification of work by “Fortyseven”/Flickr)As ?? illustrates, a transformer basically consists of two separated coils, or windings, wrapped around a soft iron core. The primary winding has ![]() loops, or turns, and is connected to an alternating voltage
loops, or turns, and is connected to an alternating voltage ![]() The secondary winding has
The secondary winding has ![]() turns and is connected to a load resistor
turns and is connected to a load resistor ![]() We assume the ideal case for which all magnetic field lines are confined to the core so that the same magnetic flux permeates each turn of both the primary and the secondary windings. We also neglect energy losses to magnetic hysteresis, to ohmic heating in the windings, and to ohmic heating of the induced eddy currents in the core. A good transformer can have losses as low as
We assume the ideal case for which all magnetic field lines are confined to the core so that the same magnetic flux permeates each turn of both the primary and the secondary windings. We also neglect energy losses to magnetic hysteresis, to ohmic heating in the windings, and to ohmic heating of the induced eddy currents in the core. A good transformer can have losses as low as ![]() of the transmitted power, so this is not a bad assumption.
of the transmitted power, so this is not a bad assumption.
(Figure 12.6.3) ![]()
To analyze the transformer circuit, we first consider the primary winding. The input voltage ![]() is equal to the potential difference induced across the primary winding. From Faraday’s law, the induced potential difference is
is equal to the potential difference induced across the primary winding. From Faraday’s law, the induced potential difference is ![]() where
where ![]() is the flux through one turn of the primary winding. Thus,
is the flux through one turn of the primary winding. Thus,
![]()
Similarly, the output voltage ![]() delivered to the load resistor must equal the potential difference induced across the secondary winding. Since the transformer is ideal, the flux through every turn of the secondary winding is also
delivered to the load resistor must equal the potential difference induced across the secondary winding. Since the transformer is ideal, the flux through every turn of the secondary winding is also ![]() and
and
![]()
Combining the last two equations, we have
Hence, with appropriate values for ![]() and
and ![]() the input voltage
the input voltage ![]() may be “stepped up”
may be “stepped up” ![]() or “stepped down”
or “stepped down” ![]() to
to ![]() the output voltage. This is often abbreviated as the transformer equation,
the output voltage. This is often abbreviated as the transformer equation,
which shows that the ratio of the secondary to primary voltages in a transformer equals the ratio of the number of turns in their windings. For a step-up transformer, which increases voltage and decreases current, this ratio is greater than one; for a step-down transformer, which decreases voltage and increases current, this ratio is less than one.
From the law of energy conservation, the power introduced at any instant by ![]() to the primary winding must be equal to the power dissipated in the resistor of the secondary circuit; thus,
to the primary winding must be equal to the power dissipated in the resistor of the secondary circuit; thus,
![]()
When combined with Equation 12.6.1, this gives
(12.6.3) ![]()
If the voltage is stepped up, the current is stepped down, and vice versa.
Finally, we can use ![]() along with Equation 12.6.1 and Equation 12.6.3, to obtain
along with Equation 12.6.1 and Equation 12.6.3, to obtain
![Rendered by QuickLaTeX.com \[v_P(t)=i_P\left[\left(\frac{N_P}{N_S}\right)^2R_S\right],\]](https://openpress.usask.ca/app/uploads/quicklatex/quicklatex.com-30bd7a222af011eb2ab31577a82b195b_l3.png)
which tells us that the input voltage ![]() “sees” not a resistance
“sees” not a resistance ![]() but rather a resistance
but rather a resistance
![]()
Our analysis has been based on instantaneous values of voltage and current. However, the resulting equations are not limited to instantaneous values; they hold also for maximum and rms values.
EXAMPLE 12.6.1
A Step-Down Transformer
A transformer on a utility pole steps the rms voltage down from ![]() to
to ![]() (a) What is the ratio of the number of secondary turns to the number of primary turns? (b) If the input current to the transformer is
(a) What is the ratio of the number of secondary turns to the number of primary turns? (b) If the input current to the transformer is ![]() what is the output current? (c) Determine the power loss in the transmission line if the total resistance of the transmission line is
what is the output current? (c) Determine the power loss in the transmission line if the total resistance of the transmission line is ![]() (d) What would the power loss have been if the transmission line was at
(d) What would the power loss have been if the transmission line was at ![]() the entire length of the line, rather than providing voltage at
the entire length of the line, rather than providing voltage at ![]() ? What does this say about transmission lines?
? What does this say about transmission lines?
Strategy
The number of turns related to the voltages is found from Equation 12.6.1. The output current is calculated using Equation 12.6.3.
Solution
a. Using Equation 12.6.1 with rms values ![]() and
and ![]() we have
we have
![]()
so the primary winding has ![]() times the number of turns in the secondary winding.
times the number of turns in the secondary winding.
b. From Equation 12.6.3, the output rms current ![]() is found using the transformer equation with current
is found using the transformer equation with current
such that
![]()
c. The power loss in the transmission line is calculated to be
![]()
d. If there were no transformer, the power would have to be sent at ![]() to work for these houses, and the power loss would be
to work for these houses, and the power loss would be
![]()
Therefore, when power needs to be transmitted, we want to avoid power loss. Thus, lines are sent with high voltages and low currents and adjusted with a transformer before power is sent into homes.
Significance
This application of a step-down transformer allows a home that uses ![]() outlets to have
outlets to have ![]() available to draw upon. This can power many devices in the home.
available to draw upon. This can power many devices in the home.
CHECK YOUR UNDERSTANDING 12.9
A transformer steps the line voltage down from ![]() to
to ![]() so that a current of
so that a current of ![]() can be delivered to a doorbell. (a) What is the ratio of the number of turns in the primary and secondary windings? (b) What is the current in the primary winding? (c) What is the resistance seen by the
can be delivered to a doorbell. (a) What is the ratio of the number of turns in the primary and secondary windings? (b) What is the current in the primary winding? (c) What is the resistance seen by the ![]() source?
source?
Candela Citations
- Download for free at http://cnx.org/contents/7a0f9770-1c44-4acd-9920-1cd9a99f2a1e@8.1. Retrieved from: http://cnx.org/contents/7a0f9770-1c44-4acd-9920-1cd9a99f2a1e@8.1. License: CC BY: Attribution

