10.4 Induced Electric Fields
LEARNING OBJECTIVES
- Connect the relationship between an induced emf from Faraday’s law to an electric field, thereby showing that a changing magnetic flux creates an electric field
- Solve for the electric field based on a changing magnetic flux in time
The fact that emfs are induced in circuits implies that work is being done on the conduction electrons in the wires. What can possibly be the source of this work? We know that it’s neither a battery nor a magnetic field, for a battery does not have to be present in a circuit where current is induced, and magnetic fields never do work on moving charges. The answer is that the source of the work is an electric field ![]() that is induced in the wires. The work done by
that is induced in the wires. The work done by ![]() in moving a unit charge completely around a circuit is the induced emf
in moving a unit charge completely around a circuit is the induced emf ![]() ; that is,
; that is,
where ![]() represents the line integral around the circuit. Faraday’s law can be written in terms of the induced electric field as
represents the line integral around the circuit. Faraday’s law can be written in terms of the induced electric field as
There is an important distinction between the electric field induced by a changing magnetic field and the electrostatic field produced by a fixed charge distribution. Specifically, the induced electric field is nonconservative because it does net work in moving a charge over a closed path, whereas the electrostatic field is conservative and does no net work over a closed path. Hence, electric potential can be associated with the electrostatic field, but not with the induced field. The following equations represent the distinction between the two types of electric field:
(10.4.3) 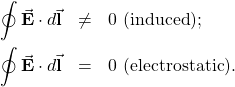
Our results can be summarized by combining these equations:
EXAMPLE 10.4.1
Induced Electric Field in a Circular Coil
What is the induced electric field in the circular coil of Example 10.2.1 (and ??) at the three times indicated?
Strategy
Using cylindrical symmetry, the electric field integral simplifies into the electric field times the circumference of a circle. Since we already know the induced emf, we can connect these two expressions by Faraday’s law to solve for the induced electric field.
Solution
The induced electric field in the coil is constant in magnitude over the cylindrical surface, similar to how Ampere’s law problems with cylinders are solved. Since ![]() is tangent to the coil,
is tangent to the coil,
![]()
When combined with Equation 10.4.4, this gives
![]()
The direction of ![]() is counterclockwise, and
is counterclockwise, and ![]() circulates in the same direction around the coil. The values of
circulates in the same direction around the coil. The values of ![]() are
are

Significance
When the magnetic flux through a circuit changes, a nonconservative electric field is induced, which drives current through the circuit. But what happens if ![]() in free space where there isn’t a conducting path? The answer is that this case can be treated as if a conducting path were present; that is, nonconservative electric fields are induced wherever
in free space where there isn’t a conducting path? The answer is that this case can be treated as if a conducting path were present; that is, nonconservative electric fields are induced wherever ![]() , whether or not there is a conducting path present.
, whether or not there is a conducting path present.
These nonconservative electric fields always satisfy Equation 10.4.4. For example, if the circular coil of Equation 10.2.3 were removed, an electric field in free space at ![]() would still be directed counterclockwise, and its magnitude would still be
would still be directed counterclockwise, and its magnitude would still be ![]() at
at ![]() ,
, ![]() at
at ![]() , etc. The existence of induced electric fields is certainly not restricted to wires in circuits.
, etc. The existence of induced electric fields is certainly not restricted to wires in circuits.
EXAMPLE 10.4.2
Electric Field Induced by the Changing Magnetic Field of a Solenoid
Part (a) of Figure 10.4.1 shows a long solenoid with radius ![]() and
and ![]() turns per unit length; its current decreases with time according to
turns per unit length; its current decreases with time according to ![]() . What is the magnitude of the induced electric field at a point a distance
. What is the magnitude of the induced electric field at a point a distance ![]() from the central axis of the solenoid (a) when
from the central axis of the solenoid (a) when ![]() and (b) when
and (b) when ![]() [see part (b) of Figure 10.4.1]. (c) What is the direction of the induced field at both locations? Assume that the infinite-solenoid approximation is valid throughout the regions of interest.
[see part (b) of Figure 10.4.1]. (c) What is the direction of the induced field at both locations? Assume that the infinite-solenoid approximation is valid throughout the regions of interest.
(Figure 10.4.1) ![]()
Strategy
Using the formula for the magnetic field inside an infinite solenoid and Faraday’s law, we calculate the induced emf. Since we have cylindrical symmetry, the electric field integral reduces to the electric field times the circumference of the integration path. Then we solve for the electric field.
Solution
a. The magnetic field is confined to the interior of the solenoid where
![]()
Thus, the magnetic flux through a circular path whose radius ![]() is greater than
is greater than ![]() , the solenoid radius, is
, the solenoid radius, is
![]()
The induced field ![]() is tangent to this path, and because of the cylindrical symmetry of the system, its magnitude is constant on the path. Hence, we have
is tangent to this path, and because of the cylindrical symmetry of the system, its magnitude is constant on the path. Hence, we have
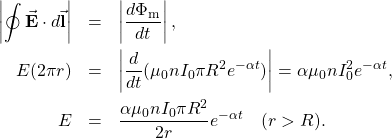
b. For a path of radius ![]() inside the solenoid,
inside the solenoid, ![]() , so
, so
![]()
and the induced field is
![]()
c. The magnetic field points into the page as shown in part (b) and is decreasing. If either of the circular paths were occupied by conducting rings, the currents induced in them would circulate as shown, in conformity with Lenz’s law. The induced electric field must be so directed as well.
Significance
In part (b), note that ![]() increases with
increases with ![]() inside and decreases as
inside and decreases as ![]() outside the solenoid, as shown in Figure 10.4.2.
outside the solenoid, as shown in Figure 10.4.2.
(Figure 10.4.2) ![]()
 . When
. When 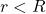 , the electric field rises linearly, whereas when
, the electric field rises linearly, whereas when  , the electric field falls of proportional to
, the electric field falls of proportional to 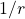 .
.CHECK YOUR UNDERSTANDING 10.6
Suppose that the coil of Example 10.2.1 is a square rather than circular. Can Equation 10.3.2 be used to calculate (a) the induced emf and (b) the induced electric field?
CHECK YOUR UNDERSTANDING 10.7
What is the magnitude of the induced electric field in Example 10.4.2 at ![]() if
if ![]() ,
, ![]() ,
, ![]() turns per metre,
turns per metre, ![]() , and
, and ![]() ?
?
CHECK YOUR UNDERSTANDING 10.8
The magnetic field shown below is confined to the cylindrical region shown and is changing with time. Identify those paths for which ![]() .
.
CHECK YOUR UNDERSTANDING 10.9
A long solenoid of cross-sectional area ![]() is wound with
is wound with ![]() turns of wire per centimetre. It is placed in the middle of a closely wrapped coil of
turns of wire per centimetre. It is placed in the middle of a closely wrapped coil of ![]() turns and radius
turns and radius ![]() , as shown below. (a) What is the emf induced in the coil when the current through the solenoid is decreasing at a rate
, as shown below. (a) What is the emf induced in the coil when the current through the solenoid is decreasing at a rate ![]() ? (b) What is the electric field induced in the coil?
? (b) What is the electric field induced in the coil?
Candela Citations
- Download for free at http://cnx.org/contents/7a0f9770-1c44-4acd-9920-1cd9a99f2a1e@8.1. Retrieved from: http://cnx.org/contents/7a0f9770-1c44-4acd-9920-1cd9a99f2a1e@8.1. License: CC BY: Attribution

