Chapter 12 Review

Samuel J. Ling; Jeff Sanny; William Moebs; Daryl Janzen

Chapter 12 Review

Key Terms

ac current
current that fluctuates sinusoidally with time at a fixed frequency

ac voltage
voltage that fluctuates sinusoidally with time at a fixed frequency

alternating current (ac)
flow of electric charge that periodically reverses direction

average power
time average of the instantaneous power over one cycle

bandwidth
range of angular frequencies over which the average power is greater than one-half the maximum value of the average power

capacitive reactance
opposition of a capacitor to a change in current

direct current (dc)
flow of electric charge in only one direction

impedance
ac analog to resistance in a dc circuit, which measures the combined effect of resistance, capacitive reactance, and inductive reactance

inductive reactance
opposition of an inductor to a change in current

phase angle
amount by which the voltage and current are out of phase with each other in a circuit

power factor
amount by which the power delivered in the circuit is less than the theoretical maximum of the circuit due to voltage and current being out of phase

quality factor
dimensionless quantity that describes the sharpness of the peak of the bandwidth; a high quality factor is a sharp or narrow resonance peak

resonant frequency
frequency at which the amplitude of the current is a maximum and the circuit would oscillate if not driven by a voltage source

rms current
root mean square of the current

rms voltage
root mean square of the voltage

step-down transformer
transformer that decreases voltage and increases current

step-up transformer
transformer that increases voltage and decreases current

transformer
device that transforms voltages from one value to another using induction

transformer equation
equation showing that the ratio of the secondary to primary voltages in a transformer equals the ratio of the number of turns in their windings

Key Equations

AC voltage	$v=V_0\sin\omega t$
AC current	$i=I_0\sin\omega t$
capacitive reactance	$\frac{V_0}{I_0}=\frac{1}{\omega C}=X_C$
rms voltage	$V_{\mathrm{rms}}=\frac{V_0}{\sqrt{2}}$
rms current	$I_{\mathrm{rms}}=\frac{I_0}{\sqrt{2}}$
inductive reactance	$\frac{V_0}{I_0}=\omega L=X_L$
Phase angle of an ac circuit	$\phi=\tan^{-1}\frac{X_L-X_C}{R}$
AC version of Ohm’s law	$I_0=\frac{V_0}{Z}$
Impedance of an ac circuit	$Z=\sqrt{R^2+(X_L-X_C)^2}$
Average power associated with a circuit element	$P_{\mathrm{ave}}=\frac{1}{2}I_0V_0\cos\phi$
Average power dissipated by a resistor	$P_{\mathrm{ave}}=\frac{1}{2}I_0V_0I_{\mathrm{rms}}V_{\mathrm{rms}}=I_{\mathrm{rms}}^2R$
Resonant angular frequency of a circuit	$\omega_0=\sqrt{\frac{1}{LC}}$
Quality factor of a circuit	$Q=\frac{\omega_0}{\Delta\omega}$
Quality factor of a circuit in terms of the circuit parameters	$Q=\frac{\omega_0L}{R}$
Transformer equation with voltage	$\frac{V_S}{V_P}=\frac{N_S}{N_P}$
Transformer equation with current	$I_S=\frac{N_P}{N_S}I_P$

Summary

12.1 AC Sources

Direct current (dc) refers to systems in which the source voltage is constant.
Alternating current (ac) refers to systems in which the source voltage varies periodically, particularly sinusoidally.
The voltage source of an ac system puts out a voltage that is calculated from the time, the peak voltage, and the angular frequency.
In a simple circuit, the current is found by dividing the voltage by the resistance. An ac current is calculated using the peak current (determined by dividing the peak voltage by the resistance), the angular frequency, and the time.

12.2 Simple AC Circuits

For resistors, the current through and the voltage across are in phase.
For capacitors, we find that when a sinusoidal voltage is applied to a capacitor, the voltage follows the current by one-fourth of a cycle. Since a capacitor can stop current when fully charged, it limits current and offers another form of ac resistance, called capacitive reactance, which has units of ohms.
For inductors in ac circuits, we find that when a sinusoidal voltage is applied to an inductor, the voltage leads the current by one-fourth of a cycle.
The opposition of an inductor to a change in current is expressed as a type of ac reactance. This inductive reactance, which has units of ohms, varies with the frequency of the ac source.

12.3 RLC Series Circuits with AC

An 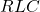$RLC$ series circuit is a resistor, capacitor, and inductor series combination across an ac source.
The same current flows through each element of an 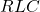$RLC$ series circuit at all points in time.
The counterpart of resistance in a dc circuit is impedance, which measures the combined effect of resistors, capacitors, and inductors. The maximum current is defined by the ac version of Ohm’s law.
Impedance has units of ohms and is found using the resistance, the capacitive reactance, and the inductive reactance.

12.4 Power in an AC Circuit

The average ac power is found by multiplying the rms values of current and voltage.
Ohm’s law for the rms ac is found by dividing the rms voltage by the impedance.
In an ac circuit, there is a phase angle between the source voltage and the current, which can be found by dividing the resistance by the impedance.
The average power delivered to an 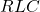$RLC$ circuit is affected by the phase angle.
The power factor ranges from 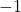$-1$ to $1$ .

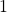12.5 Resonance in an AC Circuit

At the resonant frequency, inductive reactance equals capacitive reactance.
The average power versus angular frequency plot for a 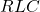$RLC$ circuit has a peak located at the resonant frequency; the sharpness or width of the peak is known as the bandwidth.
The bandwidth is related to a dimensionless quantity called the quality factor. A high quality factor value is a sharp or narrow peak.

12.6 Transformers

Power plants transmit high voltages at low currents to achieve lower ohmic losses in their many kilometers of transmission lines.
Transformers use induction to transform voltages from one value to another.
For a transformer, the voltages across the primary and secondary coils, or windings, are related by the transformer equation.
The currents in the primary and secondary windings are related by the number of primary and secondary loops, or turns, in the windings of the transformer.
A step-up transformer increases voltage and decreases current, whereas a step-down transformer decreases voltage and increases current.

Answers to Check Your Understanding

12.1 $10~\mathrm{ms}$

12.2 a. $(20~\mathrm{V})\sin200\pi t$ , $(0.20~\mathrm{A})\sin200\pi t$ ; b. $(20~\mathrm{V})\sin200\pi t$ , $(0.13~\mathrm{A})\sin(200\pi t+\pi/2)$ ; c. $(20~\mathrm{V})\sin200\pi t$ , $(2.1~\mathrm{A})\sin(200\pi t-\pi/2)$

12.3 $v_R=(V_0R/Z)\sin(\omega t-\phi)$ ; $v_C=(V_0X_C/Z)\sin(\omega t-\phi+\pi/2)=-(V_0X_C/Z)\cos(\omega t-\phi)$ ; $v_L=(V_0X_L/Z)\sin(\omega t-\phi+\pi/2)=(V_0X_L/Z)\cos(\omega t-\phi)$

12.4 $v(t)=(10.0~\mathrm{V})\sin90\pi t$

12.5 $2.00~\mathrm{V}$ ; $10.01~\mathrm{V}$ ; $8.01~\mathrm{V}$

12.6 a. $160~\mathrm{Hz}$ ; b. $40~\Omega$ ; c. $(0.25~\mathrm{A})\sin10^3t$ ; d. $0.023~\mathrm{rad}$

12.7 a. halved; b. halved; c. same

12.8 $v(t)=(0.14~\mathrm{V})\sin(4.0\times10^2t)$

12.9 a. $12:1$ ; b. $0.042~\mathrm{A}$ ; c. $2.6\times10^3~\Omega$

Conceptual Questions

12.1 AC Sources

1. What is the relationship between frequency and angular frequency?

12.2 Simple AC Circuits

2. Explain why at high frequencies a capacitor acts as an ac short, whereas an inductor acts as an open circuit.

12.3 RLC Series Circuits with AC

3. In an $RLC$ series circuit, can the voltage measured across the capacitor be greater than the voltage of the source? Answer the same question for the voltage across the inductor.

12.4 Power in an AC Circuit

4. For what value of the phase angle $\phi$ between the voltage output of an ac source and the current is the average power output of the source a maximum?

5. Discuss the differences between average power and instantaneous power.

6. The average ac current delivered to a circuit is zero. Despite this, power is dissipated in the circuit. Explain.

7. Can the instantaneous power output of an ac source ever be negative? Can the average power output be negative?

8. The power rating of a resistor used in ac circuits refers to the maximum average power dissipated in the resistor. How does this compare with the maximum instantaneous power dissipated in the resistor?

12.6 Transformers

9. Why do transmission lines operate at very high voltages while household circuits operate at fairly small voltages?

10. How can you distinguish the primary winding from the secondary winding in a step-up transformer?

11. Battery packs in some electronic devices are charged using an adapter connected to a wall socket. Speculate as to the purpose of the adapter.

12. Will a transformer work if the input is a dc voltage?

13. Why are the primary and secondary coils of a transformer wrapped around the same closed loop of iron?

Problems

12.1 AC Sources

14. Write an expression for the output voltage of an ac source that has an amplitude of $12~\mathrm{V}$ and a frequency of $200~\mathrm{Hz}.$

12.2 Simple AC Circuits

15. Calculate the reactance of a $5.0{\text -}\mu\mathrm{F}$ capacitor at (a) $60~\mathrm{Hz},$ (b) $600~\mathrm{Hz},$ and (c) $6000~\mathrm{Hz}.$

16. What is the capacitance of a capacitor whose reactance is $10~\Omega$ at $60~\mathrm{Hz}$ ?

17. Calculate the reactance of a $5.0{\text -}\mathrm{mH}$ inductor at (a) $60~\mathrm{Hz},$ (b) $600~\mathrm{Hz},$ and (c) $6000~\mathrm{Hz}.$

18. What is the self-inductance of a coil whose reactance is $10~\Omega$ at $60~\mathrm{Hz}$ ?

19. At what frequency is the reactance of a $20{\text -}\mu\mathrm{F}$ capacitor equal to that of a $10{\text -}\mathrm{mH}$ inductor?

20. At $1000~\mathrm{Hz},$ the reactance of a $5.0{\text -}\mathrm{mH}$ inductor is equal to the reactance of a particular capacitor. What is the capacitance of the capacitor?

21. A $50{\text -}\Omega$ resistor is connected across the emf $v(t)=(120~\mathrm{V})\sin(120\pi t).$ Write an expression for the current through the resistor.

22. A $25{\text -}\mu\mathrm{F}$ capacitor is connected to an emf given by $v(t)=(160~\mathrm{V})\sin(120\pi t).$ (a) What is the reactance of the capacitor? (b) Write an expression for the current output of the source.

23. A $100{\text -}\mathrm{mH}$ inductor is connected across the emf of the preceding problem. (a) What is the reactance of the inductor? (b) Write an expression for the current through the inductor.

12.3 RLC Series Circuits with AC

24. What is the impedance of a series combination of a $50{\text -}\Omega$ resistor, a $5.0{\text -}\mu\mathrm{F}$ capacitor, and a $10{\text -}\mu\mathrm{F}$ capacitor at a frequency of $2.0~\mathrm{kHz}$ ?

25. A resistor and capacitor are connected in series across an ac generator. The emf of the generator is given by $v(t)=V_0\cos\omega t,$ where $V_0=120~\mathrm{V},$ $\omega=120\pi~\mathrm{rad/s},$ $R=400~\Omega,$ and $C=4.0~\mu\mathrm{F}.$ (a) What is the impedance of the circuit? (b) What is the amplitude of the current through the resistor? (c) Write an expression for the current through the resistor. (d) Write expressions representing the voltages across the resistor and across the capacitor.

26. A resistor and inductor are connected in series across an ac generator. The emf of the generator is given by $v(t)=V_0\cos\omega t,$ where $V_0=120~\mathrm{V}$ and $\omega=120\pi~\mathrm{rad/s}$ ; also, $R=400~\Omega$ and $L=1.5~\mathrm{H}.$ (a) What is the impedance of the circuit? (b) What is the amplitude of the current through the resistor? (c) Write an expression for the current through the resistor. (d) Write expressions representing the voltages across the resistor and across the inductor.

27. In an $RLC$ series circuit, the voltage amplitude and frequency of the source are $100~\mathrm{V}$ and $500~\mathrm{Hz},$ respectively, an $R=500~\Omega,$ $L=0.20~\mathrm{H},$ and $C=2.0~\mu\mathrm{F}.$ (a) What is the impedance of the circuit? (b) What is the amplitude of the current from the source? (c) If the emf of the source is given by $v(t)=(100~\mathrm{V})\sin1000\pi t,$ how does the current vary with time? (d) Repeat the calculations with $C=0.20~\mu\mathrm{F}.$

28. An $RLC$ series circuit with $R=600~\Omega,$ $L=30~\mathrm{mH},$ and $C=0.050~\mu\mathrm{F}$ is driven by an ac source whose frequency and voltage amplitude are $500~\mathrm{Hz}$ and $50~\mathrm{V},$ respectively. (a) What is the impedance of the circuit? (b) What is the amplitude of the current in the circuit? (c) What is the phase angle between the emf of the source and the current?

29. For the circuit shown below, what are (a) the total impedance and (b) the phase angle between the current and the emf? (c) Write an expression for $i(t).$

Figure shows a circuit with a voltage source 170 V, sine 120 pi t, a resistor of 5 ohm, a capacitor of 400 microfarad and an inductor of 25 milihenry all connected in series.

12.4 Power in an AC Circuit

30. The emf of an ac source is given by $v(t)=V_0\sin\omega t,$ where $V_0=100~\mathrm{V}$ and $\omega=200\pi~\mathrm{rad/s}.$ Calculate the average power output of the source if it is connected across (a) a $20{\text -}\mu\mathrm{F}$ capacitor, (b) a $20{\text -}\mathrm{mH}$ inductor, and (c) a $50{\text -}\Omega$ resistor.

31. Calculate the rms currents for an ac source is given by $v(t)=V_0\sin\omega t,$ where $V_0=100~\mathrm{V}$ and $\omega=200\pi~\mathrm{rad/s}$ when connected across (a) a $20{\text -}\mu\mathrm{F}$ capacitor, (b) a $20{\text -}\mathrm{mH}$ inductor, and (c) a $50{\text -}\Omega$ resistor.

32. A $40{\text -}\mathrm{mH}$ inductor is connected to a $60{\text -}\mathrm{Hz}$ AC source whose voltage amplitude is $50~\mathrm{V}.$ If an AC voltmeter is placed across the inductor, what does it read?

33. For an $RLC$ series circuit, the voltage amplitude and frequency of the source are $100~\mathrm{V}$ and $500~\mathrm{Hz},$ respectively; $R=500~\Omega$ ; and $L=0.20~\mathrm{H}.$ Find the average power dissipated in the resistor for the following values for the capacitance: (a) $C=2.0~\mu\mathrm{F}$ and (b) $C=0.20~\mu\mathrm{F}.$

34. An ac source of voltage amplitude $10~\mathrm{V}$ delivers electric energy at a rate of $0.80~\mathrm{W}$ when its current output is $2.5~\mathrm{A}.$ What is the phase angle $\phi$ between the emf and the current?

35. An $RLC$ series circuit has an impedance of $60~\Omega$ and a power factor of $0.50,$ with the voltage lagging the current. (a) Should a capacitor or an inductor be placed in series with the elements to raise the power factor of the circuit? (b) What is the value of the capacitance or self-inductance that will raise the power factor to unity?

12.5 Resonance in an AC Circuit

36. (a) Calculate the resonant angular frequency of an $RLC$ series circuit for which $R=20~\Omega,$ $L=75~\mathrm{mH},$ and $C=4.0~\mu\mathrm{F}.$ (b) If $R$ is changed to $300~\Omega,$ what happens to the resonant angular frequency?

37. The resonant frequency of an $RLC$ series circuit is $2.0\times10^3~\mathrm{Hz}.$ If the self-inductance in the circuit is $5.0~\mathrm{mH},$ what is the capacitance in the circuit?

38. (a) What is the resonant frequency of an $RLC$ series circuit with $R=20~\Omega,$ $L=2.0~\mathrm{mH},$ and $C=4.0~\mu\mathrm{F}$ ? (b) What is the impedance of the circuit at resonance?

39. For an $RLC$ series circuit, $R=100~\Omega,$ $L=150~\mathrm{mH},$ and $C=0.25~\mu\mathrm{F}.$ (a) If an ac source of variable frequency is connected to the circuit, at what frequency is maximum power dissipated in the resistor? (b) What is the quality factor of the circuit?

40. An ac source of voltage amplitude $100~\mathrm{V}$ and variable frequency $f$ drives an $RLC$ series circuit with $R=10~\Omega,$ $L=2.0~\mathrm{mH},$ and $C=25~\mu\mathrm{F}.$ (a) Plot the current through the resistor as a function of the frequency $f.$ (b) Use the plot to determine the resonant frequency of the circuit.

41. (a) What is the resonant frequency of a resistor, capacitor, and inductor connected in series if $R=100~\Omega,$ $L=2.0~\mathrm{H},$ and $C=5.0~\mu\mathrm{F}$ ? (b) If this combination is connected to a $100{\text -}\mathrm{V}$ source operating at the constant frequency, what is the power output of the source? (c) What is the $Q$ of the circuit? (d) What is the bandwidth of the circuit?

42. Suppose a coil has a self-inductance of $20.0~\mathrm{H}$ and a resistance of $200~\Omega.$ What (a) capacitance and (b) resistance must be connected in series with the coil to produce a circuit that has a resonant frequency of $100~\mathrm{Hz}$ and a $Q$ of $10$ ?

43. An ac generator is connected to a device whose internal circuits are not known. We only know current and voltage outside the device, as shown below. Based on the information given, what can you infer about the electrical nature of the device and its power usage?

Figure shows an AC source connected to a box labeled Z. The source is 170V, cos 120 pi t. The current through the circuit is 0.5 Amp, cos parentheses 120 pi t plus pi by 4 parentheses.

12.6 Transformers

44. A step-up transformer is designed so that the output of its secondary winding is $2000~\mathrm{V}$ (rms) when the primary winding is connected to a $110{\text -}\mathrm{V}$ (rms) line voltage. (a) If there are $100~\mathrm{turns}$ in the primary winding, how many turns are there in the secondary winding? (b) If a resistor connected across the secondary winding draws an rms current of $0.75~\mathrm{A},$ what is the current in the primary winding?

45. A step-up transformer connected to a $110{\text -}\mathrm{V}$ line is used to supply a hydrogen-gas discharge tube with $5.0~\mathrm{kV}$ (rms). The tube dissipates $75~\mathrm{W}$ of power. (a) What is the ratio of the number of turns in the secondary winding to the number of turns in the primary winding? (b) What are the rms currents in the primary and secondary windings? (c) What is the effective resistance seen by the $110{\text -}\mathrm{V}$ source?

46. An ac source of emf delivers $5.0~\mathrm{mW}$ of power at an rms current of $2.0~\mathrm{mA}$ when it is connected to the primary coil of a transformer. The rms voltage across the secondary coil is $20~\mathrm{V}.$ (a) What are the voltage across the primary coil and the current through the secondary coil? (b) What is the ratio of secondary to primary turns for the transformer?

47. A transformer is used to step down $110~\mathrm{V}$ from a wall socket to $9.0~\mathrm{V}$ for a radio. (a) If the primary winding has $500~\mathrm{turns},$ how many turns does the secondary winding have? (b) If the radio operates at a current of $500~\mathrm{mA},$ what is the current through the primary winding?

48. A transformer is used to supply a $12{\text -}\mathrm{V}$ model train with power from a $110{\text -}\mathrm{V}$ wall plug. The train operates at $50~\mathrm{W}$ of power. (a) What is the rms current in the secondary coil of the transformer? (b) What is the rms current in the primary coil? (c) What is the ratio of the number of primary to secondary turns? (d) What is the resistance of the train? (e) What is the resistance seen by the $110{\text -}\mathrm{V}$ source?

Additional Problems

49. The emf of an dc source is given by $v(t)=V_0\sin\omega t,$ where $V_0=100~\mathrm{V}$ and $\omega=200\pi~\mathrm{rad/s}.$ Find an expression that represents the output current of the source if it is connected across (a) a $20{\text -}\mu\mathrm{F}$ capacitor, (b) a $20{\text -}\mathrm{mH}$ inductor, and (c) a $50{\text -}\Omega.$ resistor.

50. A $700{\text -}\mathrm{pF}$ capacitor is connected across an ac source with a voltage amplitude of $160~\mathrm{V}$ and a frequency of $20~\mathrm{kHz}.$ (a) Determine the capacitive reactance of the capacitor and the amplitude of the output current of the source. (b) If the frequency is changed to $60~\mathrm{Hz}$ while keeping the voltage amplitude at $160~\mathrm{V},$ what are the capacitive reactance and the current amplitude?

51. A $20{\text -}\mathrm{mH}$ inductor is connected across an AC source with a variable frequency and a constant-voltage amplitude of $9.0~\mathrm{V}.$ (a) Determine the reactance of the circuit and the maximum current through the inductor when the frequency is set at $20~\mathrm{kHz}.$ (b) Do the same calculations for a frequency of $60~\mathrm{Hz}.$

52. A $30{\text -}\mu\mathrm{F}$ capacitor is connected across a $60{\text -}\mathrm{Hz}$ ac source whose voltage amplitude is $50~\mathrm{V}.$ (a) What is the maximum charge on the capacitor? (b) What is the maximum current into the capacitor? (c) What is the phase relationship between the capacitor charge and the current in the circuit?

53. A $7.0{\text -}\mathrm{mH}$ inductor is connected across a $60{\text -}\mathrm{Hz}$ ac source whose voltage amplitude is $50~\mathrm{V}.$ (a) What is the maximum current through the inductor? (b) What is the phase relationship between the current through and the potential difference across the inductor?

54. What is the impedance of an $RLC$ series circuit at the resonant frequency?

55. What is the resistance $R$ in the circuit shown below if the amplitude of the ac through the inductor is $4.24~\mathrm{A}$ ?

Figure shows a circuit with an AC source of 50 V, sine 120 pi t. This is connected to an inductor of 8 mH, a capacitor of 400 mu F and a resistor R. Another capacitor is connected in parallel with the first one. The value of this is 200 mu F.

56. An ac source of voltage amplitude $100~\mathrm{V}$ and frequency $1.0~\mathrm{kHz}$ drives an $RLC$ series circuit with $R=20~\Omega,$ $L=4.0~\mathrm{mH},$ and $C=50~\mu\mathrm{F}.$ (a) Determine the rms current through the circuit. (b) What are the rms voltages across the three elements? (c) What is the phase angle between the emf and the current? (d) What is the power output of the source? (e) What is the power dissipated in the resistor?

57. In an $RLC$ series circuit, $R=200~\Omega,$ $L=1.0~\mathrm{H},$ $C=50~\mu\mathrm{F},$ $V_0=120~\mathrm{V},$ and $f=50~\mathrm{Hz}.$ What is the power output of the source?

58. A power plant generator produces $100~\mathrm{A}$ at $15~\mathrm{kV}$ (rms). A transformer is used to step up the transmission line voltage to $150~\mathrm{kV}$ (rms). (a) What is rms current in the transmission line? (b) If the resistance per unit length of the line is $8.6\times10^{-8}~\Omega/\mathrm{m},$ what is the power loss per meter in the line? (c) What would the power loss per meter be if the line voltage were $15~\mathrm{kV}$ (rms)?

59. Consider a power plant located $25~\mathrm{km}$ outside a town delivering $50~\mathrm{MW}$ of power to the town. The transmission lines are made of aluminum cables with a $7~\mathrm{cm}^2$ cross-sectional area. Find the loss of power in the transmission lines if it is transmitted at (a) $200~\mathrm{kV}$ (rms) and (b) $120~\mathrm{V}$ (rms).

60. Neon signs require $12{\text -}\mathrm{kV}$ for their operation. A transformer is to be used to change the voltage from $220{\text -}\mathrm{V}$ (rms) ac to $12{\text -}\mathrm{kV}$ (rms) ac. What must the ratio be of turns in the secondary winding to the turns in the primary winding? (b) What is the maximum rms current the neon lamps can draw if the fuse in the primary winding goes off at $0.5~\mathrm{A}$ ? (c) How much power is used by the neon sign when it is drawing the maximum current allowed by the fuse in the primary winding?

Challenge Problems

61. The $335{\text -}\mathrm{kV}$ ac electricity from a power transmission line is fed into the primary winding of a transformer. The ratio of the number of turns in the secondary winding to the number in the primary winding is $N_s/N_p=1000.$ (a) What voltage is induced in the secondary winding? (b) What is unreasonable about this result? (c) Which assumption or premise is responsible?

62. A $1.5{\text -}\mathrm{k}\Omega$ resistor and $30{\text -}\mathrm{mH}$ inductor are connected in series, as shown below, across a $120{\text -}\mathrm{V}$ (rms) ac power source oscillating at $60{\text -}\mathrm{Hz}$ frequency. (a) Find the current in the circuit. (b) Find the voltage drops across the resistor and inductor. (c) Find the impedance of the circuit. (d) Find the power dissipated in the resistor. (e) Find the power dissipated in the inductor. (f) Find the power produced by the source.

Series circuit with voltage source V parentheses t parentheses, a 30 mH inductor and a 1.5 kilo ohm resistor

63. A $20{\text -}\Omega$ resistor, $50{\text -}\mu\mathrm{F}$ capacitor, and $30{\text -}\mathrm{mH}$ inductor are connected in series with an ac source of amplitude $10~\mathrm{V}$ and frequency $125~\mathrm{Hz}.$ (a) What is the impedance of the circuit? (b) What is the amplitude of the current in the circuit? (c) What is the phase constant of the current? Is it leading or lagging the source voltage? (d) Write voltage drops across the resistor, capacitor, and inductor and the source voltage as a function of time. (e) What is the power factor of the circuit? (f) How much energy is used by the resistor in $2.5~\mathrm{s}$ ?

64. A $20{\text -}\Omega$ resistor, $150{\text -}\mu\mathrm{F}$ capacitor, and $2.5{\text -}\mathrm{H}$ inductor are connected in series with an ac source of amplitude $10~\mathrm{V}$ and variable angular frequency $\omega.$ (a) What is the value of the resonance frequency $\omega_R$ ? (b) What is the amplitude of the current if $\omega=\omega_R$ ? (c) What is the phase constant of the current when $\omega=\omega_R$ ? Is it leading or lagging the source voltage, or is it in phase? (d) Write an equation for the voltage drop across the resistor as a function of time when $\omega=\omega_R.$ (e) What is the power factor of the circuit when $\omega=\omega_R$ ? (f) How much energy is used up by the resistor in $2.5~\mathrm{s}$ when $\omega=\omega_R$ ?

65. Find the reactances of the following capacitors and inductors in ac circuits with the given frequencies in each case: (a) $2{\text -}\mathrm{mH}$ inductor with a frequency $60{\text -}\mathrm{Hz}$ of the ac circuit; (b) $2{\text -}\mathrm{mH}$ inductor with a frequency $600{\text -}\mathrm{Hz}$ of the ac circuit; (c) $20{\text -}\mathrm{mH}$ inductor with a frequency $6{\text -}\mathrm{Hz}$ of the ac circuit; (d) $20{\text -}\mathrm{mH}$ inductor with a frequency $60{\text -}\mathrm{Hz}$ of the ac circuit; (e) $2{\text -}\mathrm{mF}$ capacitor with a frequency $60{\text -}\mathrm{Hz}$ of the ac circuit; and (f) $2{\text -}\mathrm{mF}$ capacitor with a frequency $600{\text -}\mathrm{Hz}$ of the AC circuit.

66. An output impedance of an audio amplifier has an impedance of $500~\Omega$ and has a mismatch with a low-impedance $8{\text -}\Omega$ loudspeaker. You are asked to insert an appropriate transformer to match the impedances. What turns ratio will you use, and why? Use the simplified circuit shown below.

Figure shows a transformer with more windings in the primary coil. The primary coil is connected to a voltage source through an impedance Z equal to 500 ohm. The voltage across the windings is labeled amplifier output V subscript P. The two ends of the secondary coil of the transformer are connected across a resistance of 8 ohm.

67. Show that the SI unit for capacitive reactance is the ohm. Show that the SI unit for inductive reactance is also the ohm.

68. A coil with a self-inductance of $16~\mathrm{mH}$ and a resistance of $6.0~\Omega$ is connected to an ac source whose frequency can be varied. At what frequency will the voltage across the coil lead the current through the coil by $45^{\circ}$ ?

69. An $RLC$ series circuit consists of a $50{\text -}\Omega$ resistor, a $200{\text -}\mu\mathrm{F}$ capacitor, and a $120{\text -}\mathrm{mH}$ inductor whose coil has a resistance of $20~\Omega.$ The source for the circuit has an rms emf of $240~\mathrm{V}$ at a frequency of $60~\mathrm{Hz}.$ Calculate the rms voltages across the (a) resistor, (b) capacitor, and (c) inductor.

70. An $RLC$ series circuit consists of a $10{\text -}\Omega$ resistor, an $8.0{\text -}\mu\mathrm{F}$ capacitor, and a $50{\text -}\mathrm{mH}$ inductor. A $110{\text -}\mathrm{V}$ (rms) source of variable frequency is connected across the combination. What is the power output of the source when its frequency is set to one-half the resonant frequency of the circuit?

71. Shown below are two circuits that act as crude high-pass filters. The input voltage to the circuits is $v_{\mathrm{in}},$ and the output voltage is $v_{\mathrm{out}}.$ (a) Show that for the capacitor circuit, $\frac{v_{\mathrm{out}}}{v_{\mathrm{in}}}=\frac{1}{\sqrt{1+1/\omega^2R^2C^2}},$ and for the inductor circuit, $\frac{v_{\mathrm{out}}}{v_{\mathrm{in}}}=\frac{\omega L}{\sqrt{R^2+\omega^2L^2}}.$ (b) Show that for high frequencies, $v_{\mathrm{out}}\approx v_{\mathrm{in}},$ but for low frequencies, $v_{\mathrm{out}}.$

Figure shows two circuits. The first shows a capacitor and resistor in series with a voltage source labeled V in. V out is measured across the resistor. The second circuit shows an inductor and resistor in series with a voltage source labeled V in. V out is measured across the inductor.

72. The two circuits shown below act as crude low-pass filters. The input voltage to the circuits is vinvin, and the output voltage is vout.vout. (a) Show that for the capacitor circuit, $\frac{v_{\mathrm{out}}}{v_{\mathrm{in}}}=\frac{1}{\sqrt{1+1/\omega^2R^2C^2}},$ and for the inductor circuit, $\frac{v_{\mathrm{out}}}{v_{\mathrm{in}}}=\frac{\omega L}{\sqrt{R^2+\omega^2L^2}}.$ (b) Show that for low frequencies, $v_{\mathrm{out}}\approx v_{\mathrm{in}},$ but for high frequencies, $v_{\mathrm{out}}.$

Figure shows two circuits. The first shows a capacitor and resistor in series with a voltage source labeled V in. V out is measured across the capacitor. The second circuit shows an inductor and resistor in series with a voltage source labeled V in. V out is measured across the resistor.

License

Icon for the Creative Commons Attribution 4.0 International License