7.3 Thévenin’s Theorem
LEARNING OBJECTIVES
- Find the Thévenin equivalent circuit for any linear circuit
- Calculate the maximum power that can be transferred to a load at any point in a circuit, and the value of the load resistance required to draw maximum power
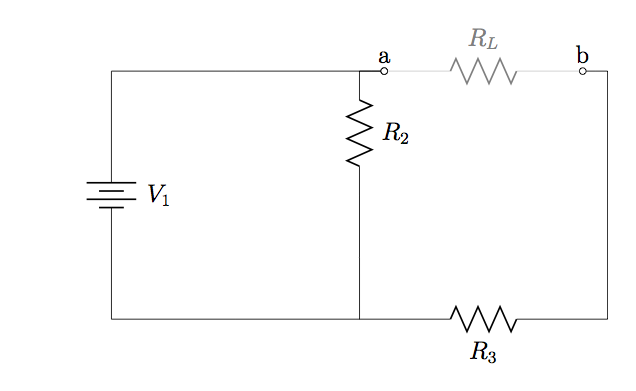
Thévenin’s theorem states that any linear circuit containing several voltage sources and resistors can be simplified to a Thévenin-equivalent circuit with a single voltage source and resistance connected in series with a load. Specifically, the three components connected in series are (see Figure 7.3.1(b)):
- Load resistor,
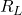 ;
; - Thévenin voltage
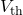 , found by removing
, found by removing 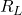 from the original circuit and calculating the potential difference from one load connection point to the other (e.g. from
from the original circuit and calculating the potential difference from one load connection point to the other (e.g. from  to
to 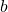 in Figure 7.3.1(a), either across
in Figure 7.3.1(a), either across 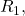
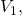 and
and 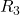 or across
or across 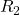 and
and 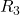 );
); - Thévenin resistance
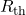 , found by removing
, found by removing 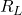 from the original circuit and calculating the total equivalent resistance between the two load connection points (e.g. between
from the original circuit and calculating the total equivalent resistance between the two load connection points (e.g. between  and
and 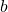 in Figure 7.3.1(a), thus as the equivalent resistance of the parallel combination of
in Figure 7.3.1(a), thus as the equivalent resistance of the parallel combination of 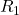 and
and 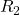 , connected in series with
, connected in series with 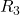 ).
).
(Figure 7.3.1) ![]()
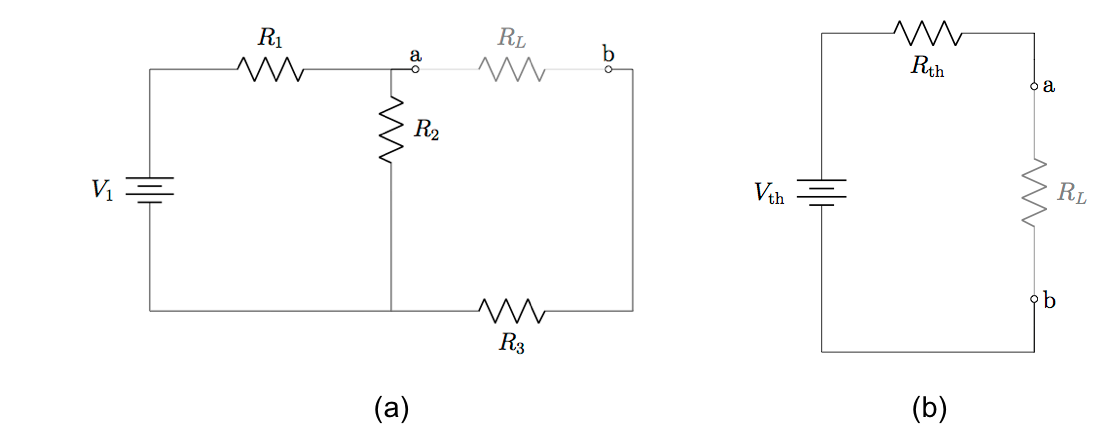
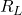 identified, and (b) its Thévenin equivalent. In fact, (b) shows the general form of all Thévenin-equivalent circuits.
identified, and (b) its Thévenin equivalent. In fact, (b) shows the general form of all Thévenin-equivalent circuits.Thévenin’s theorem is particularly useful when the load resistance in a circuit is subject to change. When the load’s resistance changes, so does the current it draws and the power transferred to it by the rest of the circuit. In fact, currents everywhere in a circuit will be subject to change whenever a single resistance changes, and the entire circuit would need to be re-analysed to find the new current through and power transferred to a load. Repeating circuit analysis to find the new current through a load every time its resistance changes would be very time-consuming. In contrast, according to Thévenin’s theorem once ![]() and
and ![]() are determined for the rest of the circuit, the current through the load is always simply calculated as
are determined for the rest of the circuit, the current through the load is always simply calculated as
(7.3.1) ![]()
from which the voltage drop across, and power transferred to the load are, respectively,
(7.3.2) ![]()
(7.3.3) ![]()
Equations 7.3.1–7.3.3 are easily applied, and the problem of repeated circuit analysis each time a load’s resistance changes is mainly reduced to the one-time problem of finding the Thévenin voltage ![]() and resistance
and resistance ![]() with respect to
with respect to ![]() . Example 7.3.1 shows the procedure for doing this for the circuit in Figure 7.3.1(a).
. Example 7.3.1 shows the procedure for doing this for the circuit in Figure 7.3.1(a).
EXAMPLE 7.3.1
Applying Thévenin’s Theorem
Find ![]() and
and ![]() for the circuit in Figure 7.3.1(a).
for the circuit in Figure 7.3.1(a).
Strategy
- Find
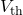 : note that with the circuit open between
: note that with the circuit open between  and
and 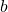 there is no current through, and therefore no voltage drop across
there is no current through, and therefore no voltage drop across 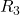 . Therefore, the potential difference between
. Therefore, the potential difference between  and
and 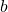 must occur in the loop containing
must occur in the loop containing 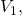
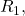 and
and 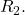 We are free to choose either parallel branch of that loop, as the potential difference across
We are free to choose either parallel branch of that loop, as the potential difference across 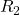 must equal the potential difference across
must equal the potential difference across 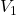 and
and 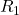 by the loop rule. Therefore, we will first determine the current in this loop and apply Ohm’s law to find
by the loop rule. Therefore, we will first determine the current in this loop and apply Ohm’s law to find 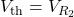 .
. - Find
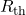 : Proceeding from
: Proceeding from  to
to 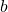 we encounter a junction where the circuit branches in two directions, towards
we encounter a junction where the circuit branches in two directions, towards 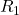 and
and 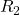 .
. 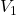 is an ideal voltage source with no resistance, and can therefore be ignored when calculating equivalent resistance. We then encounter another junction where the two branches reconnect, so
is an ideal voltage source with no resistance, and can therefore be ignored when calculating equivalent resistance. We then encounter another junction where the two branches reconnect, so 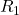 and
and 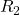 are connected in parallel. Proceeding on, we encounter
are connected in parallel. Proceeding on, we encounter 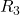 in series with the parallel connection of
in series with the parallel connection of 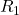 and
and 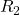 , and eventually reach
, and eventually reach 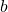 . We will add these resistances using the rules for adding series and parallel resistors.
. We will add these resistances using the rules for adding series and parallel resistors.
Solution
The current through the loop with ![]() ,
, ![]() and
and ![]() all connected in series is
all connected in series is
![]()
By Ohm’s law, the voltage across ![]() is therefore
is therefore
![]()
By our above reasoning, we therefore have
![]()
To find ![]() first write
first write
![]()
Then, by our above reasoning,
![]()
Significance
The potential difference from ![]() to
to ![]() was calculated as a drop in potential across
was calculated as a drop in potential across ![]() as current flows from the positive to the negative terminal of the voltage source
as current flows from the positive to the negative terminal of the voltage source ![]() Along the parallel branch (that is, parallel from the perspective of the load connection points
Along the parallel branch (that is, parallel from the perspective of the load connection points ![]() and
and ![]() ), potential rises at
), potential rises at ![]() , then drops across
, then drops across ![]() , travelling in the clockwise direction. By the loop rule, there must be an overall potential rise in the clockwise direction along this branch that equals negative the potential drop in the clockwise direction across
, travelling in the clockwise direction. By the loop rule, there must be an overall potential rise in the clockwise direction along this branch that equals negative the potential drop in the clockwise direction across ![]() . Thus, between
. Thus, between ![]() and
and ![]() along the left branch, travelling in the counter-clockwise direction there is also a drop in potential, equal to
along the left branch, travelling in the counter-clockwise direction there is also a drop in potential, equal to
![]()
as required.
It is important to note that perspective matters when treating components as being connected in series or parallel. Here, when determining the current through ![]() in the open circuit, we noted that current flows through a single circuit loop with
in the open circuit, we noted that current flows through a single circuit loop with ![]()
![]() and
and ![]() all connected in series, and determined the current through
all connected in series, and determined the current through ![]() as the potential drop across the series combination of resistors, divided by the equivalent resistance. However, when calculating
as the potential drop across the series combination of resistors, divided by the equivalent resistance. However, when calculating ![]() we found that from the perspective of the connection points
we found that from the perspective of the connection points ![]() and
and ![]() are connected along parallel branches of the circuit.
are connected along parallel branches of the circuit.
The procedure used here to calculate ![]() and
and ![]() is the same as that which we apply to more complex circuits. When doing so, it is important to correctly account for voltage rises and drops across between the two load connection points, although to this end we do have freedom of choice in which branch to follow and can always choose the simplest path.
is the same as that which we apply to more complex circuits. When doing so, it is important to correctly account for voltage rises and drops across between the two load connection points, although to this end we do have freedom of choice in which branch to follow and can always choose the simplest path.
CHECK YOUR UNDERSTANDING 7.3
The circuit is the same as the one from Example 7.3.1, but with ![]() replaced by a short. Determine
replaced by a short. Determine ![]() and
and ![]() in this case.
in this case.
Maximum Power Transfer Theorem
Thévenin’s theorem finds a useful application in the maximum power transfer theorem, which states that maximum power will be transferred to a load when its resistance is equal to the Thévenin resistance of the network supplying the power. This interesting and highly useful fact is easily proven by taking the derivative of Equation 7.3.3 with respect to ![]() , setting the result equal to
, setting the result equal to ![]() , and solving for the value of
, and solving for the value of ![]() that maximises the function.
that maximises the function.
![]()
![]()
![]()
EXAMPLE 7.3.2
Applying Maximum Power Transfer Theorem
What is the maximum amount of power that can be dissipated in ![]() ?
?
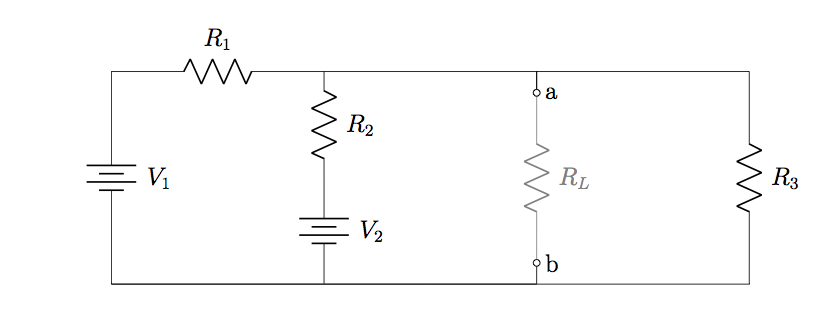
Strategy
The maximum amount of power that can be dissipated in ![]() is, by the maximum power transfer theorem, the power dissipated when
is, by the maximum power transfer theorem, the power dissipated when ![]() for the Thévenin equivalent circuit calculated with respect to
for the Thévenin equivalent circuit calculated with respect to ![]() To find this, we first determine
To find this, we first determine ![]() and
and ![]() as follows.
as follows.
With ![]() replaced by an open circuit, there are two loops: one, passing through
replaced by an open circuit, there are two loops: one, passing through ![]()
![]()
![]() and
and ![]() the other, passing through
the other, passing through ![]()
![]() and
and ![]() . We will calculate the current through
. We will calculate the current through ![]() using Mesh Analysis techniques developed earlier, then determine
using Mesh Analysis techniques developed earlier, then determine ![]() using Ohm’s law. Note that we do not actually need to calculate any other currents, since
using Ohm’s law. Note that we do not actually need to calculate any other currents, since ![]() the potential difference between
the potential difference between ![]() and
and ![]() must equal
must equal ![]() regardless which branch is taken.
regardless which branch is taken.
To find ![]() , note that with respect to connection points
, note that with respect to connection points ![]() and
and ![]() ,
, ![]()
![]() and
and ![]() are all connected in parallel.
are all connected in parallel.
Finally, when ![]() the current in the load is
the current in the load is ![]() (see Equation 7.3.1), and the power dissipated in
(see Equation 7.3.1), and the power dissipated in ![]() is
is ![]() (cf. Equation 7.3.3).
(cf. Equation 7.3.3).
Solution
Using the strategies developed in Mesh Analysis, we can write the matrix equations for this network as
![]()
where ![]() and
and ![]() are the clockwise mesh currents in the left and right loops, respectively.
are the clockwise mesh currents in the left and right loops, respectively.
To find ![]() (the actual current in
(the actual current in ![]() ), we apply Cramer’s rule:
), we apply Cramer’s rule:
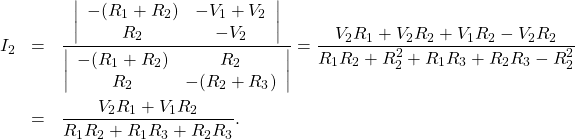
The Thévenin-equivalent voltage is therefore
![]()
The Thévenin-equivalent resistance is
![]()
Finally, the maximum power dissipated in ![]() when
when ![]() , is
, is
![]()
Significance
It is important to be clear that ![]() is the power dissipated in
is the power dissipated in ![]() only when
only when ![]() The general expression for power dissipated in
The general expression for power dissipated in ![]() is given by Equation 7.3.3.
is given by Equation 7.3.3.
Candela Citations
- Authored by: Daryl Janzen. Provided by: Department of Physics & Engineering Physics, University of Saskatchewan. License: CC BY: Attribution

