Chapter 7. Topographic Maps
Overview of Topographic Maps
7 Topographic Maps
Adapted by Joyce M. McBeth, Sean W. Lacey & Tim C. Prokopiuk (2018) University of Saskatchewan from Deline B, Harris R, & Tefend K. (2015) “Laboratory Manual for Introductory Geology”. First Edition. Chapter 3 “Topographic Maps” by Karen Tefend and Bradley Deline, CC BY-SA 4.0. View Source.
The purpose of this chapter is to familiarize students with how to read and use topographic maps. This is a critical skill to prepare students to learn about more complex geologic maps.
7.2 MAP PARTS, ORIENTATION, AND SCALE
A map is a plan view (viewed from above, also known as map view) representation of an area on Earth’s surface. Topographic maps are maps that illustrate the topography (vertical relief, such as hills) of the mapped region. Geological maps are maps that illustrate the rock types, rock ages and other geological features of the mapped area.
Every map has a:
- map area or data frame: the part of the map illustrating the map area;
- legend: a guide to the different symbols used on the map, such as lines representing roads and streams;
- scale: this defines the relationship of distances on the map to real distances in the area that the map represents;
- north arrow: indicates the direction of geographic north; and
- title: a name that generally describes the location of the map area.
The topographic and geological maps produced by Natural Resources Canada (NRCan, which includes the Geological Survey of Canada, GSC), and the United States Geological Survey (USGS) are oriented with north at the top of the map. Therefore if you move towards the top of the map you are moving in a northerly direction, and if you are moving towards the bottom of the map, you are moving towards the south. Any movement to the right or left will be towards the east or west, respectively.
7.2.1 Coordinate systems
There are two coordinate systems commonly used to define positions on Earth’s surface: geographic (latitude and longitude, abbreviated lat/long) and universal transverse mercator (UTM). Latitude and longitude coordinates are used on NRCan and USGS maps; they are simpler to interpret and plot on a map than UTM coordinates. UTM coordinates are more accurate and are used in navigation and field work. Often geologists will report coordinates of important features using both coordinate systems.
7.2.2 Geographic Coordinates
Geographic coordinates use latitude and longitude to define positions on Earth’s surface. The longitude is an imaginary line that circles the globe and is oriented so that it passes through the north and south geographic poles. Starting with the 0° longitude line (zero degrees, known as the Prime Meridian) that passes through the town of Greenwich, England, the lines of longitude increase to 180° in both directions east and west of the Prime Meridian, meeting at a line of 180° longitude that passes through the Pacific Ocean (Figure 7.1). Lines of longitude converge as you move north or south of the equator, eventually intersecting at the geographic poles.It may help to visualize longitude lines if you think of an orange, which when peeled will show the sections of orange oriented like longitude lines that section the Earth into segments.

Source: Karen Tefend (2015) CC BY-SA 3.0 view source
Lines of latitude are imaginary lines that circle the globe parallel to Earth’s equator (Figure 7.1). The 0° latitude line is the Earth’s equator, and latitude lines increase up to 90° north or 90° south of the equator. The North Pole has a latitude of 90°N, and the South Pole has a latitude of 90°S.
This grid system allows a position on Earth to be uniquely defined with a set of longitude and latitude values. The values for latitude are always identified by their position N or S of the equator, and the longitude is identified as E or W of the Prime Meridian. A degree (abbreviated with the symbol “°”) of latitude or longitude represents a large distance on Earth, therefore degrees are further subdivided into minutes, which are further subdivided into seconds. Note that a minute or second of distance is not the same as a minute or second of time. There are 60 minutes (abbreviated 60’) of distance in 1° of latitude or longitude, and there are 60 seconds (abbreviated 60”) of distance in one minute. An example of a precise location on Earth’s surface would be 52°07′ 59.00″N, 106°40′ 12.00″W (the coordinates for Saskatoon, SK). This is read as “52 degrees, 7 minutes, 59 seconds north latitude, and 106 degrees, 40 minutes, 12 seconds west longitude.” These coordinates are often converted into decimal notation. For the example above, the decimal notation coordinates are 52.133° N, 106.67° W. To convert between decimal degrees and degrees/minutes/seconds notation, use the formula: Decimal Degrees = Degrees + (Minutes / 60) + (Seconds / 3600) or use a converter on the internet (for example, on the US Federal Communications Commission website).
Note that the distance between two degrees of longitude is not the same distance in km when you are at the equator as when you are at a location in northern Canada. As the lines of longitude approach the poles of Earth, they are closer together (as illustrated in Figure 7.1), and the distance each degree, minute, and second covers is smaller. Longitudinal distances in degrees, minutes and seconds are not absolute distances like metric units are (e.g., metres).
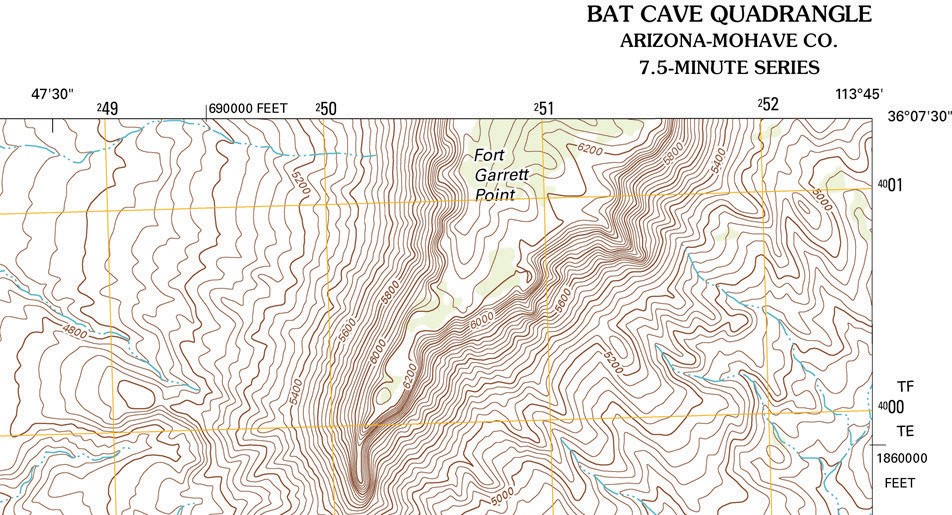
The latitude and longitude coordinates of NRCan maps are found along the edge of a map (for example see the map of Canadian geology we studied in Chapter 1). On USGS topographic maps the latitude and longitude coordinates are found at the corners of the map (Figure 7.2). Often, topographic and geological maps represent an area of Earth that is smaller than one degree of distance. Additional numbers (other than latitude and longitude) are also shown on the edges of the map (e.g., 40 01 in the top right corner of Figure 7.2); these are coordinates in the UTM grid system.
The top and bottom edges of USGS topographic maps are oriented parallel to lines of latitude. This is also broadly the case for NRCan maps; however, the closer the map area is to the north pole the more the curve of the lines of latitude will influence the distances between points on the map (since the closer to the pole, the smaller the regions defined by the lines of latitude and longitude). Near the north pole, the map may have quite different distances at the top and the bottom, particularly for maps that cover large areas. In some NRCan maps the lines of latitude curve to prevent distorting the distances between the lines of longitude (e.g., the map of Canada’s geology from Chapter 1).
In Figure 7.2, the top edge of the map is a latitude line, so the coordinates that are changing as you move along the top of the map (in an East-West direction) must be longitude coordinates, since the latitude does not change. The bottom edge of this map is not shown, but you can predict what the latitude on the bottom edge should be: this map is of a region in Arizona, and since Arizona is located north of the Equator the latitude lines should increase from the bottom of the map towards the top of the map (as all latitude lines increase as you move north of the Equator).
7.2.3 Projections
To define two-dimensional (2D) coordinates on a three-dimensional (3-D) surface, the three-dimensional surface must be converted to a 2-D surface representing the 3-D surface. This is called a projection. Whenever a 3-D object is rendered in 2-D, there is distortion. In other words, distances between positions will not always be accurate, especially for positions closer to Earth’s poles. There are different methods of rendering regions of Earth onto maps that attempt to deal with such distortion, but distortion cannot be eliminated. The typical global map of Earth is generated by wrapping a cylinder around a globe representation of Earth, with the edges of the cylinder oriented vertically, so that the edge of the cylinder touches the globe along the equator. We then imagine a light source at the centre of the globe that casts shadows of all of the globe’s features onto the inside surface of the cylinder. These shadows are then traced onto the inner surface. Unwrapping the cylinder then shows a two dimensional map of Earth. This type of projection is called a transverse Mercator map projection.
Since the equator was in contact with the inner surface of the cylinder, there is no distortion of features along the equator. But the further away from the equator you move, the more distorted the map becomes. This can see this distortion by examining a typical world map, which are usually created using a transverse Mercator map projection. On this kind of map, Greenland will appear to be a similar size to South America, but in reality, South America is nine times larger than Greenland. Also note on maps with this kind of projection you never reach 90o latitude either north or south. This is because light emanating from the globe will be moving almost parallel to the edges of the cylinder when it escapes from the globe at and near the geographic poles. Another distortion in these maps is the appearance of Antarctica as a continuous land mass that runs along the southern edge of the map. Antarctica is a circular land mass centred around the south geographic pole, rather than a long narrow island as seems to be indicated on the map.
The scale of the map is another factor that leads to distortion on maps of Earth. As you move northwards or southwards from the equator, the scale of the map expands. For example, if you use a ruler to measure 1 cm of distance at the equator, this will convert to a certain distance on the ground. But 1 cm measured further north or south of the equator will convert to larger and larger distances on the ground, depending upon how far north or south you go.
A strategy used to minimize distortion on maps is to zoom in and only render a small region of Earth’s surface into the 2-D map. The smaller the region, the less distortion will occur on the map.
7.2.4 UTM coordinates
The UTM coordinate system is another system for determining points on Earth’s surface. You will not use the UTM coordinate system in the lab exercises in this chapter, but it is important to be aware that this other coordinate system exists since it is broadly used by geoscientists in the field and in navigation. The reason the UTM system was developed was to allow for more precise calculations of positions on Earth’s surface for navigational purposes. Longitudinal degree distances change as you approach the poles of the Earth due to the curvature of Earth’s surface, resulting in distortion of distances on maps in these regions. Thus, it is difficult to make an accurate calculation of positions for navigation using latitude/longitude coordinates in northern regions. The UTM system uses a slightly different approach to map out regions on Earth’s surface to decrease the amount of distortion on maps using this grid system.
The UTM system divides the Earth into 60 zones that are 6° of longitude wide. Zones 7 to 22 cover Canada. The polar regions of Earth’s surface are not included in the UTM system, so points north of 84°N do not have UTM coordinates (note that this is further north than the most northerly islands in the Canadian Arctic). Within each zone, there is a central meridian (line of longitude) and there are 3° of longitude on either side of this central meridian. Positions within each zone are defined by how far north of the equator they are (their “northing” value), and their position relative to the central meridian of each zone (the “easting” value). The central meridian of each zone is given a value of 500,000 m. In practice, points east of a zone’s central meridian will have easting values that are less than 500,000, and points west of the central meridian will have easting values greater than 500,000.
The most important thing to remember when using UTM coordinates is that you must specify the zone for any position you are reporting, otherwise you will not be able to accurately find the position on Earth’s surface, since the easting position is not measured relative to the Prime Meridian. Here is an example of a UTM coordinate position for the University of Saskatchewan, Saskatoon, SK: UTM Zone 13U, 388107.09 E, 5776949.85 N.
7.2.4 Map scale
All maps are a scaled-down version of the region of the world that they depict; if this were not the case, then the map that a person must carry would be the exact same size as a city (if it is a city map) or the size of a province (if it is a provincial map). The word “scale” refers to the amount of reduction the map represents, and all maps include at least one type of map scale to indicate the relationship between the area on the map and the area of the region it represents in reality. Map scales are provided so that a map reader can determine exactly how much distance is actually represented on their map, or to measure the distance between two points on a map, or even to calculate the gradient (slope) of a hill or river. The two commonly used map scales on a topographic map are the bar scale (or graphical scale) and the fractional scale (also known as the ratio scale).
In Figure 7.3 there are three bar scales; each bar is a graphical representation of distance on the map, and it is up to the map reader to decide if they want to measure distances in kilometers, meters, miles, or feet. Notice that each bar scale has the starting point (zero) within the interior of the scale, and not on the end of each scale (Figure 7.3).

The other type of map scale is the fractional scale (e.g., in Figure 7.3 the fractional scale is 1:24,000). No units are reported for fractional scales because the ratio of a fractional scale is valid for any unit of measure, provided that it is the same unit on both sides of the ratio. For example, if using centimetres, then this map scale indicates that 1 cm on the map is equivalent to 24,000 cm on the ground the map represents (the distance between two locations in the real world). If our map was the same size as the area that it is representing (say for example, a map of the room you are currently sitting in), then the fractional scale of your map would be 1:1 and the map would be the exact same size as the room. This brings us again to the definition of a map, which is a scaled-down version of the region it represents. Maps that are greatly scaled down (greatly reduced) are called small scale maps even though they represent large sections of Earth. For example, a 1:500,000 map will show a large section of Earth, but small details are lost (such as building locations or small streets), whereas a 1:12,000 map is a large-scale map even though it shows a much smaller region of Earth’s surface, but greater detail can be seen (such as buildings, roads, and other landmarks).
7.3 CONTOUR LINES
Contour lines allow us to add a vertical dimension to a plan view map. Contour lines represent elevations above sea level at specific intervals within a map area. Since each individual contour line connects points of equal elevation, if you were to follow a contour line across a map area in the real world you would be walking at the same elevation while walking along that imaginary line. If you were to move off that line, you would be either walking up or down in elevation.
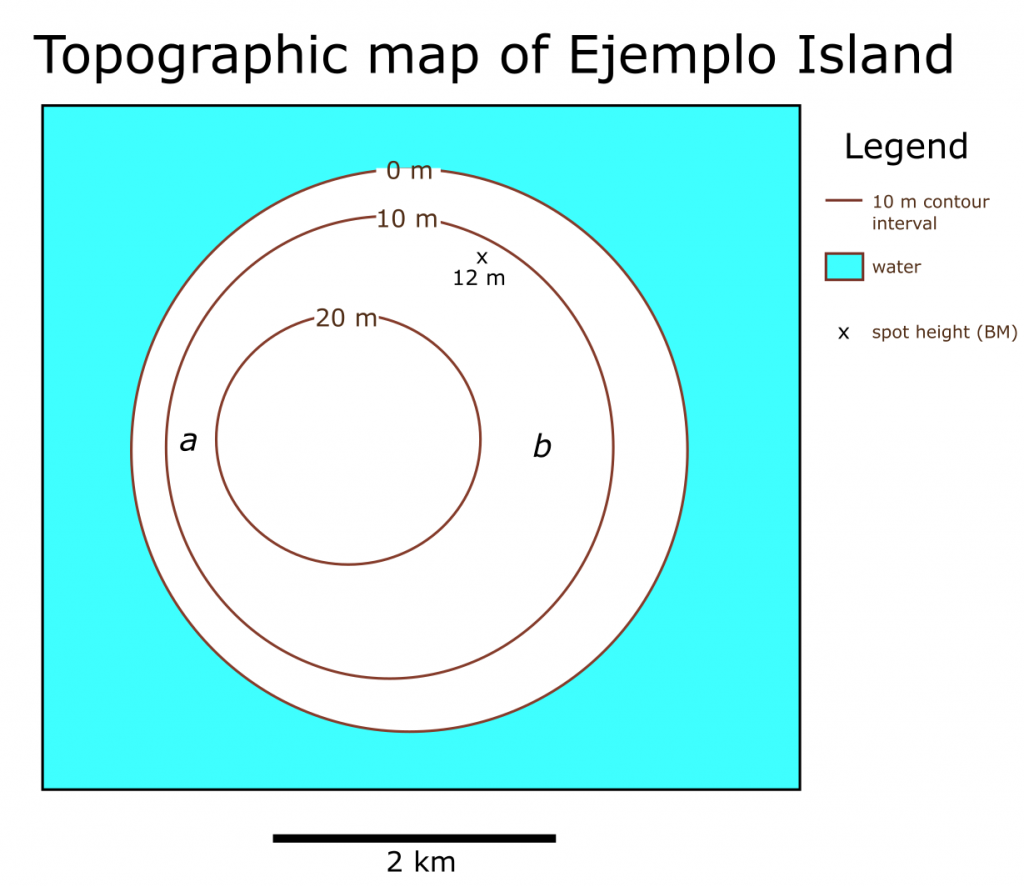
Let’s explore the concept of contour lines with an exercise. You can use a pencil and paper to illustrate this exercise as you do it. Imagine if you are on a small circular island in the ocean, and you walk from the shore up to 10 m above the shoreline. If you were to walk around the island and stay exactly 10 m above shore, you would be walking a contour line that represents 10 m of elevation above sea level. If you move off that line, you are either moving uphill or downhill. If you could walk uphill another 10 m from your first 10 m contour line, and if you stay at that elevation (20 m above sea level) while circling the island, then you have walked the 20 m contour line. The vertical change in elevation between these two adjacent contour lines is called the contour interval, which in this case is 10 m. If you were to transfer these imaginary lines onto a map, you would see three lines forming concentric circles that represent 0 m (the seashore or sea level), 10 m and 20 m, and your map would look like a bull’s eye pattern. Congratulations, you’ve made your first topographic map! If you would like to see what the map should look like, refer to Figure 7.7 at the end of this overview chapter.
Contour lines on topographic maps are shown as brown or black lines, and all maps will have a contour interval that is specific for that map. Note that the elevations represented by the contour lines are not always labeled on each line (e.g., Figure 7.2). Instead, every 5th contour line is labelled with an elevation, and is darker than the contour lines that lie between; these darker contour lines are called index contours. The use of index contours allows a map to be easier to read and is also more appealing visually, especially when the contour lines are numerous and closely spaced to one another. The reason they appear every 5th contour line is because generally index contours are every 10, 50, 100, 500, or 1000 m or feet, so the index contours are evenly spaced between these distances (i.e., every 2, 10, 20, 100, or 200 m or feet, respectively).
To determine the elevation of each contour line you must first know the contour interval for the map. By using the values of two adjacent index contours, one can easily calculate the contour interval between each line. For example, there are four contour lines between the 5200 ft and 5400 ft index contours on Figure 7.2, which means that there are four contour lines separating the 200 ft of elevation between the index contours. These divide up that 200 ft of elevation change into five sections of equal elevation change. If we divide 200 ft by five sections, each intermediate contour interval represents a 40 ft elevation change (in this example, the contours are 5200, 5240, 5280, 5320, 5360, and 5400 ft). To verify this, locate the 5200 ft index contour on the western side of the map in Figure 7.2, and increase the elevation by 40 ft each time you cross a contour line while traveling east (to the right) towards the 5400 ft contour line. Luckily there is no need to do this calculation to find the contour interval on a complete topographic map, as all topographic maps give the contour interval at the bottom of the map near the bar and fractional scales (see Figure 7.3). The contour interval must be obeyed for each contour line on a map. For example, if the contour interval is 50 m, then an example of possible contour lines on such a map would be 50 m, 100 m, 150 m, 200 m, and so on; you would not expect to see the contour interval suddenly switching on the map to 240 m, since that is not a multiple of 50 m.
You may be wondering why some contour lines are closely spaced in some areas of a map (e.g., the central portion of Figure 7.2) and why they are farther apart in other areas of a map (e.g., the western part of Figure 7.2). Let’s return to our circular island exercise: if you are standing at 10 m above sea level on the island (on the 10 m contour line) and want to walk up the hill to reach the 20 m elevation contour, how far do you have to walk? The answer is – it depends! If the hill has a gentle slope you may have to walk a long time before you reach a higher elevation of 20 m. On a topographic map, the contour lines for a gently sloping hill would be spaced far apart, because the distances between the contours are further apart horizontally. Conversely, if the hill’s slope is very steep, you do not need to walk as far up the hill to reach the 20 m elevation contour. The contour lines representing a steep slope will be closely spaced on a topographic map. Even for a perfectly circular island you could have differences in the slope of the hill between the contours (you can experiment with drawing different slopes for your island if you want to!) The slope (also known as a gradient or grade) is the change in elevation divided by the distance. you can calculate the slope of a hill or any region on a topographic map if you know the change in elevation between two points, and if you know the distance between those same two points (rise/run). Slope gradients are usually reported in meters per kilometer (m/km) but other units are sometimes used. Two common units often used are the angle of the slope above the horizonal plane (e.g., a slope of 30 degrees) or as a percent (commonly used to describe the slope of roads and in other civil engineering contexts, calculated using the equation 100 % x rise/run). If you are calculating the slope of a hill, remember to use the contour lines to determine the elevation difference, and the bar scale on your map to measure the separating distance.
In addition to contour lines, topographic maps will also have benchmarks (surveyed points) located in various locations on the map. These points are exact elevations above sea level that surveyors have measured, and they are commonly used to mark the elevations of mountains, hilltops, road intersections and airport runways. These benchmarks are rarely located on a contour line and instead are usually identified by a black “x” or identified with the letters “BM”. The benchmark also shows the specific elevation at the point, often in black (in contrast to the generally brown numbers on index contours). Benchmark locations will normally be found in the area between contour lines. For example, on a map with a contour interval of 10 m, a benchmark of 236 m would be found between the 230 m and 240 m contour lines. If the map had a contour interval of 10 m, a benchmark of 236 m would be found between the 235 m and 240 m contour lines. Try placing a 12 m benchmark point on your island map illustration!
In addition to obeying the set contour interval for a map, contour lines should not branch (split) or end at a dead end inside of the mapped region. Instead these lines are continuous, although ending at the edge of the mapped region is allowed, since the edge of the map is cutting off the contour line which would carry on outside of the mapped area. Contour lines also never touch, overlap, or cross, except in certain rare instances such as if there is a vertical or overhanging cliff. In the case of a vertical cliff, the contour lines will appear to merge because they are right on top of each other when viewed from above (plan view).
The span of the third dimension (elevation) represented by contour lines on a topographic map is called the relief. The relief for a topographic map is easily calculated by finding the highest and lowest contour line elevations on the map; you then subtract the two values to determine the vertical relief represented in the map. The hardest part of calculating the relief is finding these highest and lowest elevations on the map. Start by finding the highest index contour line and continue counting lines until you reach the lowest contour line. For example, in Figure 7.2 the highest contour line is the line that runs through the letter “r” in Fort (of Fort Garrett Point). This same contour line circles back and goes through the letter “o” in Fort. The elevation of this line is 6360 ft (based on the contour interval of 40 ft). On the map in Figure 7.2, some of the index contours appear to be missing their identifying elevation numbers, however they are still easy to identify because all index contours are in bold (darkened lines). To find the lowest elevation on the map, find the lowest index contour line and continue counting lines in the downhill direction. An easy way to determine which way is downhill is to find a water feature such as a stream on the map; water is coloured blue on topographic maps, and lines representing flowing water such as rivers or streams are coloured blue. A dashed blue line such as that shown in Figure 7.2 implies that the stream is dry part of the year (this is called an intermittent or ephemeral stream). Since water collects in low spots, such as a basin (where ponds, lakes, or oceans are found) or valleys (such as a stream or river valley), then the contour lines should represent decreasing elevation as you move towards a water feature on a map. Referring back to Figure 7.2, if you examine the contours you will see that the highest portion of the map is the central portion where Fort Garrett Point is located, and that any point west, south and east of this is a downhill direction. Note that the streams are flowing away from this Fort Garrett Point region. The lowest elevation will be a contour line that is crossing the stream just before leaving the map area. Close examination of the contour lines reveals that the lowest contour line is in the lower right corner of the map; the contour line that is crossing the stream in this portion of the map represents an elevation of 4560 ft. So, for the map area shown in Figure 7.2, the relief of the map region is 6360 ft (highest contour) – 4560 ft (lowest contour) = 1800 ft.
There is a feature worthy of special note that occurs on topographic maps where flowing water such as streams and rivers erode the landscape creating small or large valleys. There is a deflection of the contour lines on a map as they cross the valley. In Figure 7.2, the contour lines form a “v” shape as they cross the water, and that the pointed end of this “v” is pointing in the upstream direction. We can use this to easily determine which way water is flowing, even if we don’t know the elevation of the contour lines on the map, because the “v” always points upstream. This is known as the Rule of Vs for Contour Lines. Notice in Figure 7.2 that the contour lines that cross the streams are pointing toward the central hill (Fort Garrett Point), which means that the streams are all flowing away from the central portion of this map and towards the edges of the map region.
There is another, more complex feature that you may occasionally observe on topographic maps that you should be prepared for: depressions (for example, sinkholes) found on Earth’s surface. If we drew contour lines for a sinkhole feature on a map which didn’t capture an index contour within it, the sinkhole depression could be misinterpreted by a map reader as a hill top – because of this we need to provide the map reader with a different contour line feature to indicate that there is a depression in the landscape. Contour lines with small perpendicular lines (called hachure marks) are used for such depressions on a topographic map. These hachures are directed inwards towards the centre of the depression. The contour interval for the map is still obeyed when contouring a depression. The only difference is that the hachure marks on the contour lines indicate that you should count down in elevation, not up, as you move towards the center of the hachured contour circles. However, if there is a depression at the top of a hill or mountain (for example, a volcanic crater), then the first contour line that is hachured must be the same elevation of the closest contour line that is not hachured. The reason for the repeat is that a person climbing the hill will reach the highest contour line, and walk a little higher still, before descending into the depression (crater), and will therefore encounter the same elevation line again while descending (see Figure 7.4).

Source: Karen Tefend (2017) CC BY-SA 3.0 view source
7.4 DRAWING CONTOUR LINES AND TOPOGRAPHIC PROFILES
Constructing a topographic map is simple if a person remembers the following rules as they draw in contour lines on their map:
- contour lines represent lines connecting points of equal elevation above sea level;
- contour lines never cross, split, or die off;
- contour intervals must be obeyed, therefore the contour line elevations can only be multiples of the contour interval; and
- contour lines make a “v” pattern as they cross streams and rivers (Rule of Vs for Contour Lines), and the “v” always points towards the upstream direction.
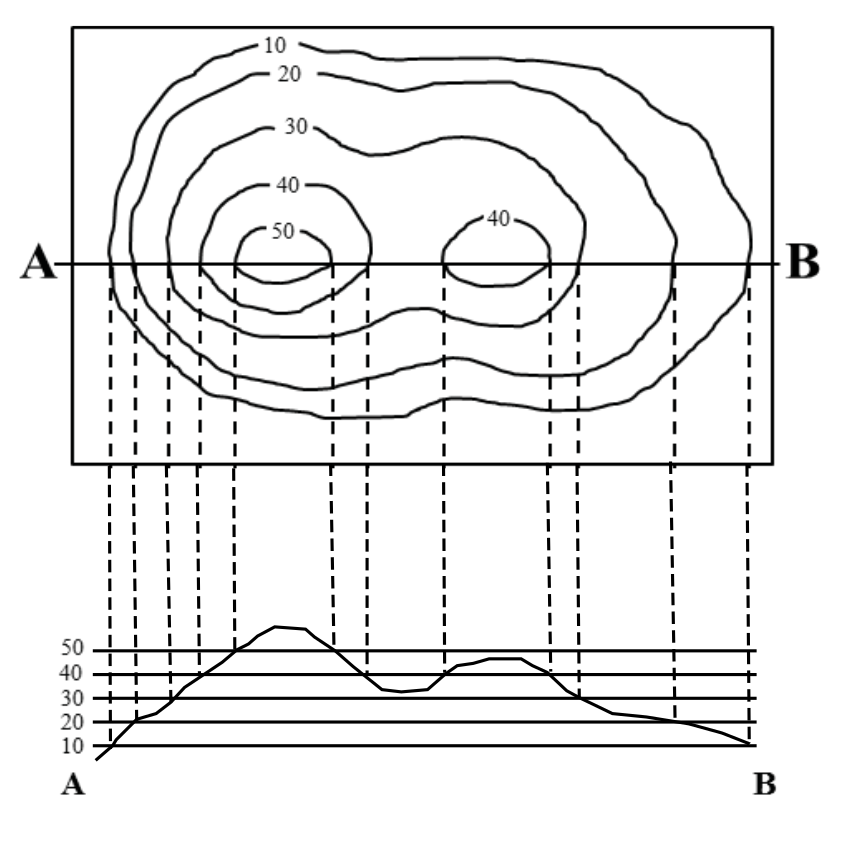
When working with topographic maps, sometimes it is useful to examine the landscape in profile. A topographic profile is a vertical cross-section or side image through a map that allows us to see how the topography varies along a line through the map. Let’s consider an example of a profile through a topographic map. The top picture in Figure 7.5 shows a topographic map of a hill that contains two separate hill tops, and the bottom picture shows a topographic profile representing the profile along the line A-B on the map. The topographic profile contains elevation lines at the same intervals as the contour lines on the topographic map, but the contour lines cut through the profile horizontally at regular intervals along the vertical axis. Note how the elevation lines are equal distances vertically as you move up through the profile. If you draw lines from the positions on the topographic profile where the contour lines reach the surface of the hill up to the same positions along the line A-B through the topographic map, they align with the contour intervals on the topographic map. This pattern is a key relationship we can use to construct topographic profiles.
7.4.1. Constructing a topographic profile
To construct a topographic profile, you need graph paper, a ruler and a pencil, and a topographic map. Use the topographic profile in Figure 7.5 as an example. Draw or select a line across the topographic map through a region of interest to you (e.g., through a hill) that you will use to draw your topographic profile (e.g., Figure 7.5 line A-B). Draw a parallel line the length of this line horizontally near the bottom of the piece of graph paper (this is the x-axis of your profile). Then draw y-axis lines on either size of the horizontal line oriented toward the top of the piece of paper. Add horizontal lines joining the two y-axes at the same intervals as the contour intervals, to represent the elevation lines. These marks should generally be at the same scale as the map (e.g., 1 cm per 10 m if the scale of the topographic map is 1:100,000). Place the profile paper between you and the line on the topographic map, with the x-axis of the profile paper parallel to the line on the topographic map (as shown in Figure 7.5). Using a ruler, you can then transfer the elevation points from where the contour lines intersect the line on your topographic map straight down onto your graph paper at the corresponding elevation lines as shown in Figure 7.5 (dashed lines). Be sure to only plot those elevations that are at the intersection of the contour line with line A-B. Once your points are plotted on the topographic profile on your graph paper, connect the dots between each contour point. You should not use straight lines to join the points – real topography is generally smoother than the jagged line produced by joining points as straight lines – use a line that gently curves through the points (Figure 7.5). Note you will have to estimate the position of the line between the points on the profile as best you can, and your line may differ from other students’ lines. That is ok if you don’t break any of the rules. As a rule, hill tops will be slightly rounded to show a slight increase in elevation to represent the crest of the hill but be careful not to draw the hill top too high on your graph paper or the profile will intersect the next elevation line – if that interval isn’t shown on the topographic map you should not go that high in the profile. For example, the first hill on the left has a top contour line of 50 m. Because there isn’t a 60 m contour line on this hill top, we know that the hill’s highest point (the crest) is some elevation between 50 and 60 m. When connecting the points on your graph paper in the area between the two hills in the Figure 7.5, you again want to round out the area to represent the base of your valley between the hills but be careful not to make the valley floor too deep, as according to the topographic map the elevation is below 40 m, but not as low as 30 m.
Source: Joyce McBeth (2018) CC BY-SA 4.0, after Karen Tefend (2015) CC BY-SA 3.0 view source
7.4.2.Vertical exaggeration
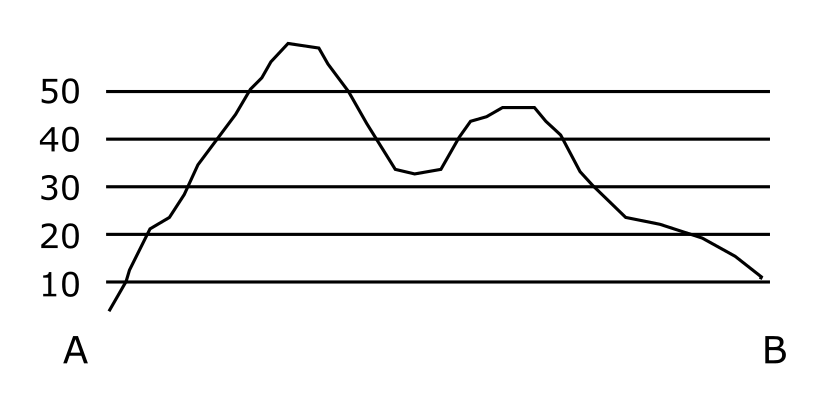
If you examine the graph showing the topographic profile in Figure 7.5, can you imagine what would happen to the profile if we changed the spacing for the elevation lines along the y-axis? When the vertical scale of the graph is larger than the horizontal scale on the map, you will end up with a graph that shows a vertical exaggeration, and the features of Earth represented by your topographic profile will become distorted. This is illustrated in Figure 7.6 which has a smaller scale for the x-axis (horizontal) than the y-axis (vertical). Sometimes vertical exaggeration is useful for illustrating features that are interesting on the topographic profile but too small to see with equal horizontal and vertical scales (e.g., small hills). To avoid creating a distorted profile, use matching vertical and horizontal scales.
Source: Joyce McBeth (2018) CC BY-SA, after Karen Tefend (2015) CC BY-SA 3.0 view source
For example, if your map scale is 1 cm = 50 m, and one centimetre on your topographic profile’s y-axis represents 50 m of elevation, there will be no vertical exaggeration in your cross-section. If 50 m on the y-axis is represented by a distance longer than 1 cm, there is vertical exaggeration in your cross-section.
Let’s explore vertical exaggeration using the topographic profiles in Figure 7.5 and 7.6. Both profiles represent the same topographic profile along line A-B on the topographic map in Figure 7.5. If the topographic map in Figure 7.5 has a fractional scale of 1:2667 then 1 cm is equal to 2667 cm or ~27 m; thus, 1 cm = 27 m for the horizontal scale on this map. If we hold a ruler to the y-axis of the topographic profile in Figure 7.5 (download and print a pdf version of this figure if you want to try this yourself) the vertical scale should also be 1 cm = 27 m since there is no vertical exaggeration in Figure 7.5. If you do the same calculation using the profile in Figure 7.6, you should find that the vertical scale is about 1 cm = 13 m. To calculate the vertical exaggeration in the topographic profile shown in Figure 7.6 we divide the vertical scale by the horizontal scale on this figure: (1 cm/13 m) / (1 cm/27 m) = 2. Therefore, the topographic profile in Figure 7.6 represents a profile along the A-B line in Figure 7.5 that has been vertically exaggerated by 2 times (2X).